સોનાના ટુકડાનું હવામાં વજન $10 \,g$ અને $9 \,g$ પાણીમાં છે તો પોલાણ (cavity) નું કદ ........ $cc$ છે. (સોનાની ઘનતા = $\left.19.3 \,g cm ^{-3}\right)$
Medium
d
(d)
(d)
When dipped in water
\(W_{\text {app }}=W_{\text {air }}-F_B\)
\(\Rightarrow 9 \,gm \times g=10 \,gm \times g-F_B\)
Where,
\(\left\{\begin{array}{l}V_c=\text { volume of cavity } \\ V_g=\text { volume of gold } \\ W_{\text {app }}=9 gm \\ W_{\text {air }}=10 gm \\ F_B=\text { force of buoyancy } \\ \rho_w=\text { density of water }=1 \\ \rho_g=\text { density of gold }=19.3\end{array}\right.\)
\(\Rightarrow 1 \times g=F_B\)
Now (total volume displaced) \(\times \rho_w \times g=1 \times g\)
\(\left(V_c+V_g\right) \times 1=1\)
\(V_c=1-\frac{\text { Mass of gold in air }}{\rho_g}=1-\frac{10}{19.3}=0.482 \,cc\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
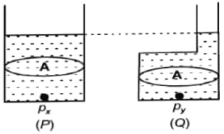
- 1આકૃતિમાં સમાન પાયાનું ક્ષેત્રફળ $A$ સાથેના બે પાત્રો $P$ અને $Q$ દર્શાવેલ છે અને દરેકને સમાન ઊંચાઈ સુધી સમાન પ્રવાહીથી ભરવામાં આવે છે. તેમને અનુરૂપ પસંદ કરો.View Solution
- 2ગુરુત્વાકર્ષણની અસર હેઠળ મુક્ત પતન કરાવવામાં આવે અને તે પાણીની ટાંકીમાં દાખલ થાય તે પહેલાં ' $h$ ' જેટલું અંતર કાપે છે. જો પાણીમાં દાખલ થયા બાદ તેનો વેગ બદલાતો ન હોય, તો $h$ નું સંનિક્ટ્ટ મૂલ્ચ ....... થશે. (પાણી માટે સ્નિગધતા $9.8 \times 10^{-6} \mathrm{~N}-\mathrm{s} / \mathrm{m}^2$ લો.)View Solution
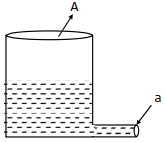
- 3એક હલકા નળાકારીય સમક્ષિતિજ સપાટી ઉપર રાખવામા આવેલ છે. તેના તળિયાનો આડછેદ $A$ છે. તેના તળિયા આગળ $a$ જેટલું આડછેદનું ક્ષેત્રફળ ધરાવતું એક છિદ્ર બનાવવામાં આવે છે. બહાર નીકળતા પ્રવાહીને કારણે લાગતાં બળને કારણે પાત્રને ન ખસેડવા માટે જરૂરી લઘુતમ ઘર્ષણાંક ............ હશે. $(a\,<\,<\,A)$View Solution
- 4બે કોપરના પાત્ર $A$ અને $B$ સમાન પાયાનું ક્ષેત્રફળ પરંતુ અલગ આકાર ધરાવે છે. એક ચોક્કસ સામાન્ય ઊંચાઈ સુધી પાણી ભરતા $A$ દ્વારા રોકતું કદ $B$ કરતાં બમણું મળે છે. તો નીચેનામાંથી સાચું વિધાન કયું છે?View Solution
- 5બે મોટા હાડકાના આડછેદના ક્ષેત્રફળ $10 \,cm ^2$ છે અને ઉપરનો ભાગ $50 \,kg$. ધરાવતા વ્યક્તિના ઉપરના ભાગ સાથે જોડેલ છે. તો સરેરાશ હાડકા વડે થતું દબાણ ......... $N / m^2$View Solution
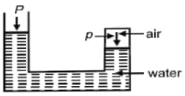
- 6મર્યાદિત હવાનું દબાણ $p$ છે. જો વાતાવરણનું દબાણ $P$ છે તો...View Solution
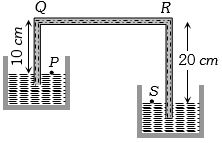
- 7પ્રવાહીની ઘનતા $ 1.5 gm/cc$ છે,તો $P$ અને $S$ બિંદુ વચ્ચે દબાણનો તફાવત કેટલો થાય?View Solution
- 8પદાર્થનું વજન હવામાં વજન કરતા પાણીમાં હવામાં વજન કરતાં ત્રીજા ભાગનું છે, તો પદાર્થ ઘનતા ............. $g / cm ^3$View Solution
- 9અનિયમિત આડછેદ ધરાવતી પાઇપમાં બે બિંદુએ ત્રિજયાનો ગુણોત્તર $3:2$ છે.તો વેગનો ગુણોત્તર કેટલો થાય?View Solution
- 10બે નાના સમાન દળના અને $\rho_{1}$ અને $\rho_{2}\left(\rho_{1}=8 \rho_{2}\right)$ ઘનતા ધરાવતા ગોળાની ત્રિજ્યા અનુક્રમે $1\; mm$ અને $2\; mm$ છે. તે બંનેને એક $\eta$ શ્યાનતાગુણાંક વાળા અને $0.1{\rho}_{2} $ ઘનતા ધરાવતા પ્રવાહીમાં (સ્થિર સ્થિતિમાંથી) પાડવામાં આવે, તો તેમના ટર્મિનલ વેગનો ગુણોત્તર કેટલો થાય?View Solution
