સ્થાનાંતરની રીતમાં બહિર્ગોળ લેન્સને પદાર્થ અને પડદાની વચ્ચે મૂકવામાં આવે છે. જો બે સ્થિતિમાં મોટવણી $m_1$ અને $m_2$ અને બે સ્થિતિ વચ્ચે લેન્સનું સ્થાનાંતર $x$ છે, તો લેન્સની કેન્દ્રલંબાઈ......છે.
Medium
b
We know in displacement method,
We know in displacement method,
\(m _1=\frac{ v }{ u }\) and
\(m _2=\frac{ u }{ V }\)
Thus, \(m_1 \times m_2=1\)
\(m _1- m _2=\frac{ v }{ u }-\frac{ u }{ v }\)
\(m _1- m _2=\frac{ V ^2- u ^2}{ uv }\)
From the figure,
Given, \(v-u=x\)
\(\Rightarrow m _1- m _2=\frac{( v + u )( v - u )}{ uv }=\frac{( v + u ) x }{ uv }\)
Using lens formula,
\(\frac{1}{f}=\frac{1}{V}-\frac{1}{u}\)
For Position 1, we have
Object Distance \(=- u\)
Image Distance \(=v\)
\(\frac{1}{f}=\frac{1}{v}-\frac{1}{-u}\)
\(\frac{1}{f}=\frac{u+v}{u v}\)
\(\Rightarrow m _1- m _2=\frac{( v + u ) x }{ uv }=\frac{1}{ f } \times x\)
\(\Rightarrow m _1- m _2=\frac{ x }{ f }\)
\(f=\frac{x}{m_1-m_2}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
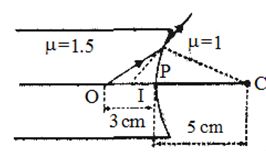
- 1આકૃતિમાં દર્શાવ્યા મુજબ એક કાચ ($\mu = 1.5$) અંદર એક હવાનો પરપોટો $10\, cm$ વ્યાસ ધરાવતી ગોળાકાર સપાટીથી $3 \,cm$ અંતરે રહેલો છે. જો સપાટી અંત:ર્ગોળ હોય તો સપાટી પરથી ......$cm$ અંતરે પરપોટો દેખાશે.View Solution
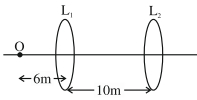
- 2એક બિંદુવત વસ્તુ $O$ ને બે પાતળા અનુક્રમે $24\,cm$ અને $9\,cm$ કેન્દ્રલંબાઈવાળા સંમિત સમઅક્ષીય લેન્સ $L _1$ અને $L _2$ ની સામે મૂકે છે. બે લેન્સ વચ્યેનું અંતર $10\,cm$ અને વસ્તુને આકૃતિમાં દર્શાવ્યા પ્રમાણે લેન્સ $L_1$ થી $6\,cm$ દૂર રહેલી છે. વસ્તુ અને બે લેન્સના તંત્ર વડે રચાતા પ્રતિબિંબ વચ્ચેનું અંતર .........$cm$ છે.View Solution
- 3એક દાઢી કરવાનો અરીસો માણસ તેનાથી $10\,cm$ અંતરે મૂકે છે અને તે પોતાનું પ્રતિબિંબ નજીકતમ અંતર $25\,cm$ અંતરે જોવે છે તો આ અરિસાની વક્રતાત્રિજ્યા કેટલા $cm$ હશે?View Solution
- 4માણસ $100 cm$ સુધી જોઇ શકે છે. તેને દૂરનું જોવા માટે કેટલા પાવરનો લેન્સ પહેરવો પડે?View Solution
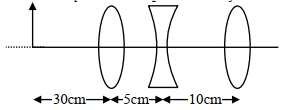
- 5લેન્સના સંયોજન વડે ૨ચાતા પ્રતિબંબનું સ્થાન. . . . . છે. $\mathrm{f}_1=10 \mathrm{~cm} \quad \mathrm{f}_2=10 \quad \mathrm{f}_3=30 \mathrm{~cm}$View Solution
- 6$20 \,cm$ કેન્દ્રલંબાઈના અંતર્ગોળ અરીસાથી $40 \,cm$ દૂર પદાર્થ મૂકેલો છે તો રચાતું પ્રતિબિંબ ......છે.View Solution
- 7એક સંયુક્ત માઈક્રોસ્કોપ $15\, cm$ અંતરે અલગ રાખેલ એક $6.25\, cm $ કેન્દ્રલંબાઈના આઈપીસ અને $ 20 \,cm$ કેન્દ્રલંબાઈના ઓબ્જેક્ટિવ લેન્સનો બનેલો છે. તો અનંત અંતરે અંતિમ પ્રતિબિંબ રચાયેલ હોય ત્યારે મેગ્નિફાઇગ પાવર કેટલો છે?View Solution
- 8એક માણસ સ્થિર સમતલ અરીસા તરફ $15 \,m/s$ થી ગતિ કરે છે. તેના પ્રતિબિંબની અરીસાના સાપેક્ષે ઝડપ .....$m/s$ છે.View Solution
- 9એક પક્ષી હવામાંથી માછલીને પાણીની અંદર જુએ છે. $h_1$ એ પક્ષીની પાણીની સપાટીથી ઉંચાઈ અને $h_2$ એ માછલીની પાણીની સપાટીથી ઉંડાઈએ છે. જો હવાની સાપેક્ષે પાણીનો વક્રીભવનાંક $\mu$ છે. ત્યારે પક્ષીએ નોંધેલું માછલીનું અંતર ......છે.View Solution
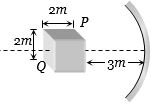
- 10$1\,m$ કેન્દ્રલંબાઇવાળા અંર્તગોળ અરીસાની સામે આકૃતિ મુજબ સમઘન મૂકેલ છે. તો $P$ અને $Q$ ના પ્રતિબિંબ વચ્ચેનું અંતર અને ઊંચાઇ કેટલી થાય?View Solution