$t = 0$ સમયે એક $r$ ત્રિજ્યા ધરાવતા ધાતુના વાહક તારની બનેલી લૂપને ચુંબકીયક્ષેત્ર $B = {B_0}{e^{\frac{{ - t}}{\tau }}}$ , ને લંબ મૂકવામાં આવે છે, જ્યાં $B_0$ અને $\tau $ અચળાંક છે$t = 0$. જો લૂપનો અવરોધ $R$ હોય તો લાંબા સમય પછી $\left( {t \to \infty } \right)$ તારમાં ઉત્પન્ન થતી ઉષ્મા કેટલી હશે?
JEE MAIN 2016, Diffcult
b
Electric flux is given by
Electric flux is given by
\(\phi=B . A\)
\(\phi=\mathrm{B}_{0} \pi \mathrm{r}^{2} \mathrm{e}^{-1 / \tau}\)
\(\left(\because B=B_{0} e^{-t / \tau}\right)\)
Induced \(E.m.f.\) \(\varepsilon=\frac{\mathrm{d} \phi}{\mathrm{dt}}=\frac{\mathrm{B}_{0} \pi \mathrm{r}^{2}}{\tau^{2}} \mathrm{e}^{-t / \tau}\)
Heat \(=\int_{0}^{\infty} \frac{\varepsilon^{2}}{\mathrm{R}}=\frac{\pi^{2} \mathrm{r}^{4} \mathrm{B}_{0}^{2}}{2 \tau \mathrm{R}}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક વર્તુળાકાર વાહક લૂપને $0.4\,T$ મૂલ્યના સમાન ચુંબકીય ક્ષેત્રમાં ક્ષેત્રને લંબ સમતલમાં મૂકેલી છે. કોઇક કારણસર $1\,mm / s$ ના અચળ દરે વિસ્તારણ શરૂ થાય છે. જ્યારે લૂપની ત્રિજ્યા $2\,cm$ થાય તે વખતે લૂપમાં પ્રેરિત થતા $emf$ નું મૂલ્ય $........\,\mu V$ હશે.View Solution
- 2View Solutionચુંબકીય ફલક્સનો એકમ ..... .
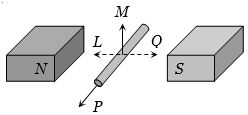
- 3View Solutionસળિયાના બે છેડા વચ્ચે વિદ્યુતસ્થિતિમાન ઉત્પન્ન કરવા માટે તેને કઈ દિશામાં ગતિ કરાવવો જોઈએ.
- 4View Solutionકઈ અવસ્થા દરમિયાન એડી પ્રવાહો જોવાં મળે છે ?
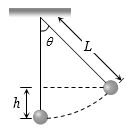
- 5$L$ લંબાઇ ધરાવતું સાદું લોલક ચુંબકીયક્ષેત્ર $B$ માં લંબ રહીને $ 2\theta $ ખૂણે દોલનો કરે છે,તો મહત્તમ $emf$ કેટલો થાય?View Solution
- 6કોઈ $10\, m$ લાંબો સમક્ષિતિજ તાર કે જે ઉત્તર-પૂર્વથી દક્ષિણ-પશ્ચિમ દિશામાં ખેંચાયેલો હોય અને પૃથ્વીના $0.3\times 10^{-4}\,Wb/m^2$ ના ચુંબકીય ક્ષેત્રના સમક્ષિતિજ ઘટકને કાટકોણે $5.0\, ms^{-1}$ ની ઝડપથી પતન કરે છે. પ્રેરિત $emf$ નું તત્ક્ષણિક મૂલ્ય કેટલું હશે.View Solution
- 7$R$ અવરોધવાળી કોઇલમાં $ \Delta t $ સમયમાં ફલક્સનો ફેરફાર $ \Delta \phi $ હોય, તો આ સમયમાં કોઇલના કોઈ બિંદુ પાસેથી કેટલો વિદ્યુતભાર $Q$ પસાર થાય?View Solution
- 8ફ્લૂરેસ્કેન્ટ લેમ્પ ચોકમાં(નાનું ટ્રાન્સ્ફોર્મર) $0.025 \;\mathrm{ms} $ માં પ્રવાહ એકસમાન રીતે $0.25 \;\mathrm{A}$ થી ઘટીને $0\;\mathrm{A}$ થાય છે ત્યારે તે $100 \;\mathrm{V}$ નો રિવર્સ વૉલ્ટેજ ઉત્પન્ન કરે છે.તો ચોકનું આત્મપ્રેરકત્વ($\mathrm{mH}$ માં) કેટલું હશે?View Solution
- 9$L = 2\,mH$ ઇન્ડકટરમાંથી પસાર થતો પ્રવાહ સમય સાથે $i = t^2e^{-t}$ મુજબ બદલાય છે. કેટલા સમયે ($sec$ માં) $e.m.f.$ શૂન્ય થાય?View Solution
- 10એક વર્તુળાકાર વાહક લૂપને તેનું સમતલ ચુંબકીય ક્ષેત્રને લંબરૂપે રહે તેમ $0.04\; T$ ના સમાન ચુંબકીય ક્ષેત્રમાં મૂકેલ છે. લૂપની ત્રિજયા $2\; mm/s$ ના અચળ દરથી સંકોચાવા લાગે છે. જ્યારે લૂપની ત્રિજયા $2 \;cm$ થાય ત્યારે લૂપમાં ઉદ્ભવતું પ્રેરિત $emf$ કેટલું હશે?View Solution
