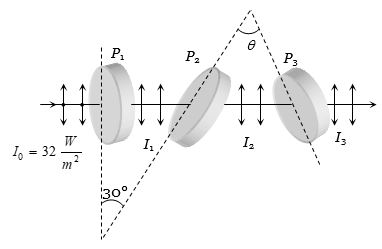
ત્રણ પોલેરાઇઝર એવી રીતે મૂકેલા છે,કે જેથી પ્રથમ અને ત્રીજી પોલેરાઇઝર - અક્ષ એકબીજાને લંબ રહે છે.પ્રથમ અને દ્રિતીય પોલેરાઇઝરની દગ- અક્ષ વચ્ચેનો ખૂણો $30^°$ છે જો પ્રથમ પોલેરાઇઝર પર $32 \frac{w}{{{m^2}}} $ તીવ્રતા ઘરાવતો અધ્રુવીભૂત પ્રકાશ આપાત કરતા ત્રીજા પોલેરાઇઝરમાંથી કેટલી તીવ્રતા ઘરાવતો પ્રકાશ......$W{m^{ - 2}}$ મળે?
Diffcult
b
(b)Angle between \(P_1\) and \(P_2\) = \(30°\) (given)
Angle between \(P_2\) and \(P_3 = \theta = 90° -30° = 60°\)
The intensity of light transmitted by \(P_1\) is \({I_1} = \frac{{{I_0}}}{2} = \frac{{32}}{2} = 1\frac{W}{{{m^2}}}\)
According to Malus law the intensity of light transmitted by \(P_2\) is \({I_2} = {I_1}{\cos ^2}30^\circ = 16\,{\left( {\frac{{\sqrt 3 }}{2}} \right)^2} = 12\,\frac{W}{{{m^2}}}\)
Similarly intensity of light transmitted by \(P_3\) is \({I_3} = {I_2}{\cos ^2}\theta = 12{\cos ^2}60^\circ = 12\,{\left( {\frac{1}{2}} \right)^2} = 3\frac{W}{{{m^2}}}\)
(b)Angle between \(P_1\) and \(P_2\) = \(30°\) (given)
Angle between \(P_2\) and \(P_3 = \theta = 90° -30° = 60°\)
The intensity of light transmitted by \(P_1\) is \({I_1} = \frac{{{I_0}}}{2} = \frac{{32}}{2} = 1\frac{W}{{{m^2}}}\)
According to Malus law the intensity of light transmitted by \(P_2\) is \({I_2} = {I_1}{\cos ^2}30^\circ = 16\,{\left( {\frac{{\sqrt 3 }}{2}} \right)^2} = 12\,\frac{W}{{{m^2}}}\)
Similarly intensity of light transmitted by \(P_3\) is \({I_3} = {I_2}{\cos ^2}\theta = 12{\cos ^2}60^\circ = 12\,{\left( {\frac{1}{2}} \right)^2} = 3\frac{W}{{{m^2}}}\)

Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionપ્રકાશ એ સુરેખ ગતિ કરે જ્યારે.
- 2View Solutionજ્યારે પ્રકાશ ઉદ્ગમને બહિગોંળ લેન્સના કેન્દ્ર આગળ રાખવામાં આવે છે ત્યારે પ્રકાશ બહિર્ગોળ લેન્સમાંથી નિર્ગમન પામે છે. પ્રકાશના તરંગઅગ્રનો આકાર. . . . . હશે.
- 3View Solutionયંગનો બે સ્લિટનો પ્રયોગ એકવર્ણીય પ્રકાશ વડે કરવામા આવે છે. એક સ્લિટની સામે પાતળી પટ્ટી રાખવામા આવે છે તો
- 4યંગના બે સ્લિટના પ્રયોગમાં પડદા પરના કોઈ એક ચોક્કસ બિંદુ પર વ્યતિકરણ પામતાં બે તરંગો વચ્ચેનો પથ તફાવત તરંગ લંબાઈનામાં $\frac{1}{8}$ ભાગનો છે. આ બિંદુ અને પ્રકાશિત શલાકાના કેન્દ્ર પરની તીવ્રતાઓનો ગુણોત્તર _____ ની નજીકનો હશે.View Solution
- 5View Solutionકયા ગુણના આધારે પ્રકાશ તરંગને ધ્વનિ તરંગથી અલગ કરી શકાય છે?
- 6View Solutionટેલિસ્કોપના વસ્તુ કાચના લેન્સનો અપર્ચર મોટો રાખવામા આવે છે કે જેથી
- 7View Solutionપ્રકાશનું વિવર્તન અડચણ (ધાર) પરથી શરૂ થાય છે. જે ......પર આધાર રાખે છે.
- 8એકરંગી સમાંતર જૂથની તરંગલંબાઇ $\lambda$ છે.જયારે સ્લિટની પહોળાઇએ પ્રકાશનો તરંગલંબાઇના ક્રમનો હોય, ત્યારે વિવર્તન રચાય છે.જો સ્લિટ અને પડદા વચ્ચેનું અંતર $D $ હોય,તો મધ્યસ્થ અધિકતમની પહોળાઇ કેટલી?View Solution
- 9યંગના બે-સ્લિટનાં પ્રયોગમાં, જ્યારે $600\,nm$ તરંગલંબાઈનો પ્રકાશાનો ઉપયોગ કરવામાં આવે છે, ત્યારે એક વિદ્યાર્થી પડદાના ચોક્કસ ભાગમાં $8$ શાલાકાઓ જુએ છે. જો પ્રકાશની તરંગલંબાઈ બદલીને $400\,nm$ કરવામાં આવે તો પડદાના તે જ ભાગમાં હવે તેને જોવા મળતી શલાકાઓની સંખ્યા$....$હશે.View Solution
- 10યંગના ડબલ સ્લીટના પ્રયોગમાં સ્લીટ અને પડદા વચ્ચેનું અંતર $1 .0\,\,m$ અને આપાત પ્રકાશની તરંગલંબાઈ $600\,\,nm$ છે. સ્લીટની પાસે રહેલ માણસ વિવર્તન ભાત જુએ છે. સ્લીટ વચ્ચેનું અંતર ફેરવવામાં આવે છે જ્યારે સ્લીટ વચ્ચેનું અંતર $d_0$ થાય ત્યારે વિવર્તન ભાત અદૃશ્ય થઈ જાય છે. જો આંખનું કોણીય વિભેદન $\frac {1}{60}^o$ હોય તો $d_0$ નું મૂલ્ય કેટલા $mm$ હશે?View Solution
