તરંગનું સમીકરણ $ y = A{\cos ^2}\left( {2\pi \;nt - 2\pi \frac{x}{\lambda }} \right) $ હોય,તો કંપવિસ્તાર આવૃત્તિ અને તરંગલંબાઇ કેટલી થાય?
Medium
a
(a) The given equation can be \(x\) written as
(a) The given equation can be \(x\) written as
\(y = \frac{A}{2}\cos \,\left( {4\pi nt - \frac{{4\pi x}}{\lambda }} \right) + \frac{A}{2}\) \(\left( \because cos^2 \theta = \frac{{1+ cos2\theta}}{{2}} \right)\)
Hence amplitude \( = \frac{A}{2}\) and frequency \( = \frac{\omega }{{2\pi }} = \frac{{4\pi n}}{{2\pi }} = 2n\)
and wave length \( = \frac{{2\pi }}{k} = \frac{{2\pi }}{{4\pi /\lambda }} = \frac{\lambda }{2}\).
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
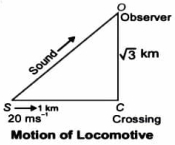
- 1ક્રોસિંગ નજીક પહોંચતી ટ્રેનની ઝડ૫ $20 \,ms ^{-1}$ છે. તે જ્યારે ક્રોસિંગથી $1 \,km$ દુર હોય ત્યારે $640 \,Hz$ આવૃતિની સીટી વગાડે છે. હવા શાંત છે અને હવામાં અવાજની ઝડપ $330\,ms ^{-1}$ છે. ક્રોસિંગથી લંબ રીતે $\sqrt{3} \,km$ દૂર ઉભેલા શ્રોતા વડે ........ $Hz$ આવૃતિ સંભળાશે.View Solution
- 2View Solutionવાયુમાં ધ્વનિની ઝડપ શેના પર આધાર રાખે?
- 3$50\,cm$ લંબાઇની એક ખુલ્લી વાંસળીની મદદથી સંગીતકાર દ્વિતીય પ્રસંવાદી ધ્વનિ તરંગો ઉત્પન્ન કરે છે. ખંડના બીજા છેડા થી એક વ્યક્તિ $10\, km/h$ ની ઝડપથી આ સંગીતકાર તરફ દોડે છે. જો તરંગની ઝડપ $330\, m/s$ છે. તો દોડતી વ્યક્તિને સંભળાતી આવૃતિ _____ $Hz$ ની નજીકની હશે.View Solution
- 4એક લંબગત તરંગને $y= Asin $ $\left( {\omega t - kx} \right)$ મુજબ દર્શાવાય છે. કઈ તરંગલંબાઇ માટે તરંગની ઝડપ અને કણની મહત્તમ ઝડપ સમાન થશે?View Solution
- 5બે તરંગ એકસાથે એક તાર પર પસાર થાય છે તેના સમીકરણ નીચે મુજબ છે.View Solution
${y}_{1}={A}_{1} \sin {k}({x}-v {t}), {y}_{2}={A}_{2} \sin {k}\left({x}-{vt}+{x}_{0}\right)$
કંપવિસ્તાર ${A}_{1}=12\, {mm}$ અને ${A}_{2}=5\, {mm}$ ${x}_{0}=3.5\, {cm}$ અને તરંગ સદીશ ${k}=6.28\, {cm}^{-1}$ આપેલ છે.
તો પરીણામી તરંગનો કંપવિસ્તાર $......\,{mm}$ થશે.
- 6$256 Hz$ આવૃત્તિના સ્વરકાંટા અને પીયાનો દ્વારા $5$ સ્પંદ પ્રતિ સેકન્ડે સંભળાય છે.પીયાનોનો તણાવ વધારતાં $2$ સ્પંદ પ્રતિ સેકન્ડે સંભળાય છે.તો પીયાનોની શરૂઆતની આવૃત્તિ કેટલી હશે?View Solution
- 7માધ્યમમાં તરંગની ઝડપ $960 \,m/sec$ છે, માધ્યમના કોઇ એક બિંદુએ $1$ મિનિટમાં પસાર થતાં તરંગોની સંખ્યા $3600$ હોય,તો તરંગની તરંગલંબાઇ કેટલી ..... $meters$ થાય?View Solution
- 8બંધ પાઇપમાં સ્થિત તરંગ $ y = 2a\sin kx\cos \omega \,t $ હોય,તો તે $ y = a\sin (\omega \,t - kx) $ અને કયાં તરંગના સંપાતીકરણના કારણે મળે ?View Solution
- 9સોનોમીટરના પ્રયોગમાં જયારે દોરી સાથે $180\,g$ વજનને લટકાવવામાં આવે છે ત્યારે તે તેની $30\,Hz$ ની મૂળભૂત આવૃત્તિ સાથે આંદોલિત થાય છે. જયારે $m$ વજનને લટકાવવામાં આવે છે ત્યારે દોરી $50\,Hz$ ની મૂળભૂત આવૃત્તિ સાથે આંદોલિત થાય છે.અહી $m$ ની કિંમત ............ $g$ છે.View Solution
- 10નકકર ધાતુના ભોયતયિળા પર $ 1\; m $ લંબાઇનો એક ધાતુનો સળિયો એકદમ શિરોલંબ છોડવામાં આવે છે.ઓસિલોસ્કોપ વડે એ શોધવામાં આવ્યું કે અથડામણ $1.2 \;kHz$ આવૃતિના સંગત તરંગ ઉત્પન્ન કરે છે. આ ધાતુના સળિયામાં ધ્વનિની ઝડપ ($m/s$ માં) કેટલી હશે?View Solution
