$U\left( r \right) = \frac{1}{2}k{r^2}$ ના કેન્દ્રીય સ્થિતિમાન ક્ષેત્રમાં એક વર્તુળાકાર કક્ષામાં $m$ દ્રવ્યમાન વાળો એક કણ ગતિ કરે છે.જો ક્વોન્ટાઇઝેશન શરતો લગાડવામાં આવે તો શક્ય કક્ષકો અને તેના ઊર્જાસ્તરો એ ક્વોન્ટમ ક્રમ (સંખ્યા) $ n$ સાથે ______ થી ચલે છે.
JEE MAIN 2019, Diffcult
a
\(\mathrm{U}=\frac{1}{2} \mathrm{kr}^{2}\)
\(\mathrm{U}=\frac{1}{2} \mathrm{kr}^{2}\)
Force, \(F=-\frac{d U}{d r}=-k r\)
For circular motion \(\frac{\mathrm{mv}^{2}}{\mathrm{r}}=\mathrm{kr}\) .... \((i)\)
And \({ mvr }=\frac{n h}{2 \pi}\) .... \((ii)\)
\({ \Rightarrow {r^2} = \frac{{{\text{nh}}}}{{2\pi \sqrt {{\text{km}}} }}}\)
\({ \Rightarrow {\text{r}} \propto \sqrt {\text{n}} }\)
Total energy, \(E=k+U\)
\( = \frac{1}{2}m{v^2} + \frac{1}{2}k{r^2}\)
\( = \frac{1}{2}k{r^2} + \frac{1}{2}k{r^2}\) [From equation \((i)\)]
\(E = k{r^2}\)
\( \Rightarrow \,\,E\, \propto \,\,n\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1હાઈડ્રોજન પરમાણુમાં $n$ મી કક્ષામાં ઈલેક્ટ્રોનની ત્રિજ્યા $ r_n$ અને કક્ષીય વેગમાન $L_n$ લો તો......View Solution
- 2હાડકમાં ફ્રેકચર શોધવામાં લઘુતમ તરંગલંબાઈ $10^{11}\,m$ હોય તો $x-ray$ મશીન માં વૉલ્ટેજ.View Solution
- 3$X-ray$ ની તરંગલંબાઈ $0.010 \ Å$ હોય તો તેનું વેગમાન કેટલું થાય?View Solution
- 4હાઇડ્રોજન પરમાણુમાં $n = 2$ અને $n = 3$ કક્ષામાં રહેલી ઊર્જાનો તફાવત $E$ હોય, તો ધરા-સ્થિતિમાં રહેલા ઇલેકટ્રોનને દૂર કરવા માટે કેટલા ........$E$ ઉર્જાની જરૂર પડે?View Solution
- 5હાઇડ્રોજન સ્પેકટ્રમના ઊર્જા સ્તરો આપેલા છે, $A,B$ અને $C$ કઇ શ્રેણી દર્શાવે છે.View Solution
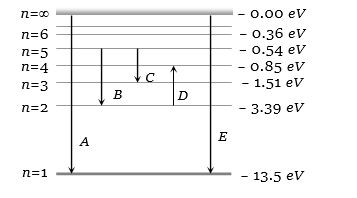
- 6હાડકમાં ફ્રેકચર શોધવામાં લઘુતમ તરંગલંબાઈ $10^{11}\,m$ હોય તો $x-ray$ મશીન માં વૉલ્ટેજ.View Solution
- 7$Li ^{++}$માં ઈલેક્ટોનને પ્રથમ કક્ષામાંથી ત્રીજી કક્ષામાં ઉત્તેજીત કરવા માટે એકરંગી પ્રકાશ કિરણનો ઉપયોગ કરવામાં આવે છે. એકરંગી પ્રકાશની તરંગલંબાઈ $x \times 10^{-10} m$ જેટલી મળે છે. $x$ નું મૂલ્ય .......... છે. [ $hc =1242 \,eV nm$ આપેલ છે.]View Solution
- 8View Solutionલાઇમન શ્રેણી અને બામર શ્રેણીની લીમીટ રેખાની આવૃત્તિનો ગુણોત્તર કેટલો થાય?
- 9$X-$ ટ્યુબમાંથી નીકળતા $X-ray$ ની લઘુતમ તરંગલંબાઈ કોના પર આધારીત છે ?View Solution
- 10હાઇડ્રોજન પરમાણુમાં જ્યારે ઇલેકટ્રોન દ્વિતીય ઉત્તેજીત અવસ્થામાંથી પ્રથમ ઉત્તેજીત અવસ્થામાં સંક્રાંતિ કરે છે ત્યારે ઉત્સર્જતા વિકિરણની તરંગલંબાઈ $\lambda_0$ હાઇડ્રોજન પરમાણુમાં ઇલેકટ્રોન જ્યારે તૃતિય ઉતેજીત અવસ્થામાંથી બીજી કક્ષામાં કૂદકો મારે ત્યારે ઉત્સર્જીત વિકિરણની તરંગલંબાઈ $\frac{20}{x} \lambda_0$ હશે. $x$ નું મૂલ્ય $...........$ થશે.View Solution
