ઉષ્માશોષક પ્રક્રિયા માટે, સક્રિયકરણની ઊર્જા $E_a$ છે અને પ્રક્રિયાની ઊર્જા એ $\Delta H$ (આ બંને $kJ/mol$ માં) છે.$E_a$નું ન્યૂનતમ મૂલ્ય હશે?
AIPMT 2010, Medium
c
In endothermic reactions, energy of reactants is less than that of the products. Potential energy diagram for endothermic reactions is
In endothermic reactions, energy of reactants is less than that of the products. Potential energy diagram for endothermic reactions is
$E_{a}= E_{a}^{\prime}+\Delta H$
where, $E_{a}=$ activation energy of forward reaction
$E_{a}^{\prime}=$ activation energy of backward reaction
$\Delta \mathrm{H}=$ enthalpy of the reaction.
From the diagram below,
$E_{a}= E_{a}^{\prime}+\Delta H$
$E_{a}>\Delta H$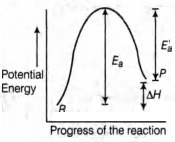
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionએસ્ટરનું એસીડીક જળ વિભાજન....... છે.
- 2કેન્દ્રિય વિખંડન દરમિયાન, નીપજો પૈકીની એક $6.93$ વર્ષ અર્ધ આયુષ્ય ધરાવતુ $^{90} \mathrm{Sr}$ છે. જો એક તાજા જન્મેલા બાળકના હાડકામાં $Ca$ ને બદલે $1 \;\mu g$ $^{90} \mathrm{Sr}$ શોષાયુ હોય અને તે ચયાપચય દ્વારા ગુમાવાતુ ન હોય તો તેમાં $90 \%$ ઘટાડો થતા કેટલો સમય, વર્ષમાં, લાગશે ?View Solution
- 3નિયત તાપમાને પ્રક્રિયાની સક્રિયકરણ ઉર્જા $2.303\,RT$ જૂલ મોલ $^{-1}$ મળે છે. તો વેગ અચળાંક અને આર્હેંનિયસ અચળાંકનો ગુણોત્તર ...... થશે.View Solution
- 4પ્રક્રિયા $A \to B$ પ્રથમ ક્રમની ગતિકીને અનુસરે છે. $A$ ના $0.8$ મોલમાંથી $B$ ના $0.6$ મોલ ઉત્પન્ન કરવા $1$ કલાક લાગે છે. તો $A$ ના $0.9$ મોલમાંથી $B$ ના $0.675$ મોલ ઉત્પન્ન કરવા .......... કલાક લાગશે .View Solution
- 5રાસાયણિક પ્રક્રિયાનો તાપમાન આધારિત વેગ અચળાંક આર્હેનિયસ સમીકરણ $K = A.{e^{ - E^*/RT}}$ ના સ્વરૂપમાં લખાય છે. તો પ્રક્રિયાની સક્રિયકરણ ઉર્જા $({E^*})$ ............... નો ગ્રાફ દોરી ગણી શકાય છે.View Solution
- 6પ્રક્રિયા $A \to B$ પ્રથમ ક્રમની ગતિકીને અનુસરે છે. $0.80\,mole\, A$ માંથી $0.60\, mole\, B$ બનવા માટે $1\, hr$ લાગે છે. તો $0.90\, mole\,A$ માંથી $0.675\, mole\, B$ બનવા માટે ........ $hr$ લાગશે.View Solution
- 7તાપમાન $300$ $K$ થી વધારી $310$ $K$ કરતા $A$ ની પ્રક્રિયાના વેગ બે ગણો થાય છે. જે $A$ કરતા $B$ ની પ્રક્રિયાની સક્રિયકરણ ઊર્જા બે ગણી હોય તો વેગ બે ગણો કરવા $B$ નું તાપમાન $300$ $K$ થી કેટલુ વધારવું જોઇએ ?View Solution
- 8$2NO + Cl_2 \rightarrow 2NOCl $ પ્રક્રિયા માટે, નીચેની કાર્ય પદ્ધતિ સૂચવે છે. તો પ્રક્રિયા માટેનો દર નિયમ...... થશે. $NO + Cl_2 $ $\rightleftharpoons$ $ NOCl_2$ (ઝડપી); $NOCl_2 + NO \rightarrow 2NOCl$ (ધીમી)View Solution
- 9પ્રથમ ક્રમ પ્રક્રિયાનો વેગ પ્રક્રિયાની શરૂઆત થયા પછી $10$ minutes પર $0.04 \mathrm{~mol} \mathrm{~L}^{-1} \mathrm{~S}^{-1}$ છે અને $20 \ minutes$ પર $0.03 \mathrm{~mol} \mathrm{~L}^{-1} \mathrm{~s}^{-1}$ છે. પ્રક્રિયાનો અર્ધ આયુષ્ય _______________ $minutes$ છે. (આપેલ : $\log 2=0.3010, \log 3=0.4771)$View Solution
- 10જો એક પ્રથમ ક્રમની પ્રક્રિયા $45$ મિનિટમાં અડધી પૂર્ણ થાય છે, તો પ્રક્રિયા $.....$ કલાકમાં $99.9\%$ પૂર્ણ થશે.View Solution
