વિધાન $- 1$ : યંગના ડબલ સ્લીટના પ્રયોગમાં વપરાતા પ્રકાશની લાંબી તરંગલંબાઈ માટે દેખાતી શલાકાની સંખ્યા ઓછી અને નાની તરંગલંબાઈ માટે દેખાતી શલાકાની સંખ્યા વધુ હોય છે.
વિધાન $- 2$ : યંગના ડબલ સ્લીટના પ્રયોગમાં દેખાતી શલાકાની સંખ્યા પ્રકાશની તરંગલંબાઈના સમપ્રમાણમાં હોય છે
JEE MAIN 2013, Easy
Download our app for free and get started
c
Fringe width \(\mathrm{B}=\frac{\mathrm{D}}{\mathrm{d}} \lambda\)
Fringe width \(\mathrm{B}=\frac{\mathrm{D}}{\mathrm{d}} \lambda\)
And number of fringes observed in the field
of view is obtaincd by \(\frac{d}{\lambda}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1બે સ્લિટો વચ્ચેનું અંતર $1\, mm$ અને પડદો $1 \,m$ દૂર રાખવામાં આવેલ છે, જ્યારે $500\, nm$ તરંગલંબાઈનો લ્યુ-ગ્રીન પ્રકાશ વાપરવામાં આવે ત્યારે શલાકાઓ વચ્ચેનું અંતર કેટલું હશે ?View Solution
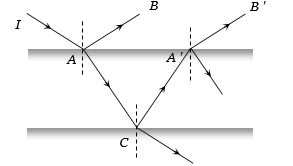
- 2દરેક પ્લેટ $25\%$ આપાત પ્રકાશની તીવ્રતાનું પરાવર્તન કરે છે. જયારે $AB$ અને $A'B'$ ને યંગના પ્રયોગની બે સ્લિટ લેવામાં આવે તો મહતમ અને ન્થૂનતમ તીવ્રતાનો ગુણોતર $ \frac {I_{\max }}{I_{\min }} $ કેટલો થાય?View Solution
- 3View Solutionનિચેનામાંથી કોના વડે વિવર્તનની ઘટના દર્શાવાાય છે.
- 4$ {I_0} $ તીવ્રતાવાળો અધ્રુવીભૂત પ્રકાશ બે પોલેરોઇડ પર આપાત કરતાં બીજા પોલેરોઇડમાંથી પ્રકાશ બહાર આવતો નથી,ત્રીજો પોલેરોઇડ પ્રથમ પોલેરોઇડની દ્ગ અક્ષ સાથે $\theta$ ખૂણે બંને પોલેરોઇડની વચ્ચે મૂકતાં અંતિમ પોલેરોઇડમાંથી બહાર આવતાં પ્રકાશની તીવ્રતા કેટલી થાય?View Solution
- 5ચાર સ્વતંત્ર તરંગો નીચેના સમીકરણોથી દર્શાવાય છે. તો ક્યા સમીકરણ વ્યતિકરણની ઘટના દર્શાવે છે?$Y_1 = a_1 \,sin\,\omega t, \,Y_2\, = a_2 \,sin\,\omega t,\, Y_3 = \,a_3\, cos\,\omega t, $ ${Y_4}\, = \,\,{a_4}\,\,\sin \,\,\,(\omega t\, + \,\,\frac{\pi }{3})$View Solution
- 6યંગના પ્રયોગમાં બે સ્લિટ વચ્ચેનું અંતર $0.5\, mm$ અને સ્લિટ અને પડદા વચ્ચેનું અંતર $0.5\, m$ છે,$5890\, A^o$ તરંગલંબાઈ ધરાવતા પ્રકાશ વાપરતા પ્રથમ અને ત્રીજી પ્રકાશિત શલાકા વચ્ચેનું અંતર શોધો.View Solution
- 7View Solutionવ્યતિકરણની ઘટના ..... થી દેખાય છે.
- 8બે સુસમ્બદ્વ ઉદ્ગમોની તીવ્રતાનો ગુણોત્તર $\alpha $ છે.$\frac{{{I_{max}} - {I_{min}}}}{{{I_{max}} + {I_{min}}}}$ નું મૂલ્ય કેટલું થાય?View Solution
- 9$I$ તીવ્રતા ધરાવતો અધ્રુવીભૂત પ્રકાશ બે પોલારાઇઝ $A$ અને $B$ ધરાવતા તંત્ર પર આપાત થાય છે. તેમાંથી બહાર આવતા પ્રકાશની તીવ્રતા $I/2$ છે જો ત્રીજા પોલારાઇઝર ને $C$ ને $A$ અને $B$ ની વચ્ચે મૂકવામાં આવે તો બહાર આવતા પ્રકાશની તીવ્રતા ઘટીને $I/3$ થાય છે. જો પોલારાઇઝ $A$ અને $C$ વચ્ચેનો ખૂણો $\theta $ હોય તો ....View Solution
- 10View Solutionવિનાશક વ્યતિકરણ માં પથ તફાવત