વર્ણપટરેખાઓની પાશ્ચન શ્રેણીમાં ટૂંકામાં ટૂંકી કઈ તરંગલંબાઈ હાજર છે?
Easy
a
Rydberg's Formula is given as:
Rydberg's Formula is given as:
\(\frac{h c}{\lambda}=21.76 \times 10^{-19}\left[\frac{1}{n_{1}^{2}}-\frac{1}{n_{2}^{2}}\right]\)
Where, \(h=\) Planck's constant \(=6.6 \times 10^{-34} \,Js\)
\(c=\) Speed of light \(=3 \times 10^{8} \,m / s\)
\((n_{1} \text { and } n_{2}\) are integers)
The shortest wavelength present in the Paschen series of the spectral lines is for values \(n_{1}=3\)
and \(n_{2}=\infty\)
\(\frac{h c}{\lambda}=21.76 \times 10^{-19}\left[\frac{1}{(3)^{2}}-\frac{1}{(\infty)^{2}}\right]\)
\(\lambda=\frac{6.6 \times 10^{-34} \times 3 \times 10^{8} \times 9}{21.76 \times 10^{-19}}\)
\(=8.189 \times 10^{-7} \,m\)
\(=818.9 \;nm\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1હાઇડ્રોજન પરમાણુ, ડ્યુરેટોન પરમાણુ, $ He^+ $આયન અને $Li^{++}$ આયન ચારેયમાં એક ઇલેકટ્રૉન તેમના ન્યુક્લિયસની આસપાસ પરિક્રમણ કરે છે. ઇલેકટ્રૉનની $n = 2 $ માંની કક્ષામાંથી $n = 1 $ મી કક્ષામાં સંક્રાંતિ થતા ઉત્સર્જાતા વિદ્યુતચુંબકીય તરંગની તરંગ-લંબાઈઓ અનુક્રમે $\lambda_1, \lambda_2$, $\lambda_3$ અને $\lambda_4$ માલૂમ પડે છે, તો ...View Solution
- 2હાઈડ્રોજન પરમાણુની $7$ મી બોહર ત્રિજ્યામાં ઈલેક્ટ્રોનની ઝડપ $3.6 \times 10^6\,m / s$ છે. તેને આનુષાગિક ત્રીજી કક્ષામાં ઈલેક્ટ્રોનની ઝડપ વેગ $........\times 10^6$ હશે.View Solution
- 3$57$ પરમાણ્વિય આંક વાળા ઘટક ની રેખા $K_\alpha$ માટે તરંગ લંબાઈ $57$ છે. $29$ પરમાણ્વિય આંક વાળા ઘટકની રેખા $K_\alpha$ માટે તરંગ લંબાઈ કેટલી હશે?View Solution
- 4પ્રવેગ આપતાં સ્થિતિમાન $V$ એ ઉત્પન થતાં ક્ષ-કિરણની લઘુતમ તરંગલંબાઈ $\lambda$ છે. જો પ્રવેગ આપતાં સ્થિતિમાનનું મુલ્ય $2 \,V$ થાય તો લઘુત્તમ તરંગલંબાઈ કેટલી થશે?View Solution
- 5$Li ^{++}$માં ઈલેક્ટોનને પ્રથમ કક્ષામાંથી ત્રીજી કક્ષામાં ઉત્તેજીત કરવા માટે એકરંગી પ્રકાશ કિરણનો ઉપયોગ કરવામાં આવે છે. એકરંગી પ્રકાશની તરંગલંબાઈ $x \times 10^{-10} m$ જેટલી મળે છે. $x$ નું મૂલ્ય .......... છે. [ $hc =1242 \,eV nm$ આપેલ છે.]View Solution
- 6$X-$ કિરણો ઉત્પન્ન કરવા માટે,$V$ વિજવિભવથી એક ઇલેકટ્રોન બીજાને પ્રવેગીત કરીને એક ઘાતુના ટાર્ગેટ પર આપાત કરવામાં આવે છે.આ સતત $( continuous)$ અને લાક્ષણિક $( characteristic)$ $ X-$ કિરણોનું ઉત્પાદન કરે છે. જો $λ_{min}$ એ $X-$ કિરણોના વર્ણપટની શકય લઘુતમ તરંગલંબાઇ હોય,તો $log$ $λ_{min}-log$ $V$ ના ફેરફારને _______ વડે સાચી રીતે રજુ કરી શકાય.View Solution
- 7$Li^{++} $ આયનની આયનીકરણ ઊર્જા ....... છે.View Solution
- 8હાઇડ્રોજન પરમાણુમાં $n = 2$ અને $n = 3$ કક્ષામાં રહેલી ઊર્જાનો તફાવત $E$ હોય, તો ધરા-સ્થિતિમાં રહેલા ઇલેકટ્રોનને દૂર કરવા માટે કેટલા ........$E$ ઉર્જાની જરૂર પડે?View Solution
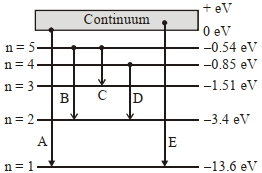
- 9આપેલ આકૃતિમાં, અમુક સંક્રાંતિઓ કે જે $A, B, C, D$ અને $E$ વડે દર્શાવેલ છે. તેની સાથે હાઈડ્રોજન પરમાણુનાં ઊર્જા સ્તરો દર્શાવ્યા છે. સંક્રાંતિઓ $A, B$ અને $C$ અનુક્રમે ,......... રજૂ કરે છેView Solution
- 10હાઈડ્રોજન પરમાણુ તેની ધરાસ્થિતિમાં $10.2 \,eV$ ઊર્જાનું શોષણ કરે છે. ઈલેકટ્રોનનું કોણીય વેગમાનનું મૂલ્ય ............... $\times 10^{-34} \; J{s}$ જેટલું વઘશે. (પ્લાન્ક અચળાંક $=6.6 \times 10^{-34} \,Js$ આપેલ છે.)View Solution
