\(\begin{array}{l}
Let\,the\,force\,F\,is\,applied\,at\,an\,angle\,\theta \\
with\,the\,horizontal.\\
For\,horizontal\,equilibrium,\,\\
F\cos \theta = \mu R\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( i \right)\\
For\,vertical\,equilibrium,\\
R + F\sin \theta = mg\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\\
or,\,R = mg - F\sin \theta \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,....\left( {ii} \right)\\
Substituting\,this\,value\,of\,R\,in\,eq.\left( i \right),
\end{array}\)
\(\begin{array}{l}
we\,get\\
F\cos = \mu \left( {mg - F\sin \theta } \right)\\
= \mu \,mg - \,\mu F\sin \theta \\
or,\,F\,\left( {\cos \theta + \mu \sin \theta } \right) = \mu mg\\
or,\,\,F = \frac{{\mu mg}}{{\cos \theta + \mu \sin \theta }}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( {iii} \right)\\
For\,F\,to\,be\,m{\rm{inimum,}}\,{\rm{the}}\,{\rm{denominator}}\\
\left( {\cos \theta + \mu \sin \theta } \right)\,should\,be\,{\rm{maximum}}.
\end{array}\)
\(\begin{array}{l}
\therefore \,\frac{d}{{d\theta }}\left( {\cos \theta + \mu \sin \theta } \right) = 0\\
or,\, - \sin \theta + \mu \cos \theta = 0\\
or,\,\tan \theta = \mu \\
or,\theta = {\tan ^{ - 1}}\left( \mu \right)\\
Then,\,\sin \theta \, = \frac{\mu }{{\sqrt {1 + {\mu ^2}} }}\,and
\end{array}\)
\(\begin{array}{l}
\cos \theta = \frac{1}{{\sqrt {1 + {\mu ^2}} }}\\
Hence,\,{F_{\min }}\\
= \frac{{\mu w}}{{\frac{1}{{\sqrt {1 + {\mu ^2}} }} + \frac{{{\mu ^2}}}{{\sqrt {1 + {\mu ^2}} }}}} = \frac{{\mu w}}{{\sqrt {1 + {\mu ^2}} }}
\end{array}\)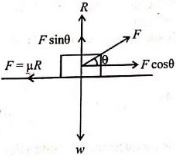
Download our appand get started for free
Similar Questions
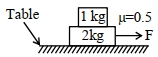
- 1બે બ્લોક વચ્ચેનો સ્થિત ઘર્ષણાંક $0.5$ અને ટેબલ લીસું છે. બંને બ્લોકને સાથે ગતિ કરાવવા માટે તેમના પર મહત્તમ કેટલું સમક્ષિતિજ બળ ($N$ માં) લગાવી શકાય? ($\left.g=10\, {ms}^{-2}\right)$View Solution
- 2સમક્ષિતિજ સપાટી પર રહેલા $10\, kg$ ના બ્લોક પર $129.4 \,N $ સમક્ષિતિજ બળ લગાવવામાં આવે છે જો ઘર્ષણાંક $0.3$ હોય તો બ્લોક ....... $m/s^2$ પ્રવેગ પ્રાપ્ત કરશે.View Solution
- 3એક કારના તળિયા પર રહેલો પદાર્થ સ્થિર રહે છે. પદાર્થ અને તળિયા વચ્યેનો સ્થિત ઘર્ષણાંક $0.15$ છે.કારનો મહત્તમ પ્રવેગ ($m s ^{-2}$ માં) ગણો.$\left( g =10\,m s ^{-2}\right)$.View Solution
- 4એક કણ વર્તુળાકાર કક્ષામાં કેન્દ્ર તરફના આકર્ષણ બળને લીધે ગતિ કરે છે જે અંતર $r$ ના વ્યસ્ત પ્રમાણમા છે તો તેની ઝડપ ...View Solution
- 5$1.96\, m$ લંબાઇ ધરાવતી દોરી સાથે $0.25 \,kg$ નો દડો બાંધીને સમક્ષિતિજ વર્તુળમાં ફેરવવામાં આવે છે. દોરીની તણાવક્ષમતા $25\,N$ છે. દડાને મહત્તમ કેટલી ઝડપથી ($m/s$ માં) ગતિ કરાવી શકાય?View Solution
- 6$40 \,m$ ત્રિજયા ધરાવતા સમતલ રોડ પર કારની મહત્તમ સલામત ઝડપ કેટલા ...........$m{s^{ - 1}}$ થશે? રોડ અને ટાયર વચ્ચેનો ઘર્ષણાંક $0.25$ છે. $( g = 10 ms^{-2})$View Solution
- 7સિમેન્ટ, પત્થર અને રેતી ને ભ્રમણ કરતાં નળાકારીય ડ્રમ માં મિશ્ર કરવાથી કોંક્રિટ મિશ્રણ બને છે. જો ડ્રમ ખૂબ જ ઝડપથી ભ્રમણ કરે તો તેમાની સામગ્રી દીવાલ સાથે ચોંટી જાય છે અને સામગ્રી નું યોગ્ય મિશ્રણ બનતું નથી. તો યોગ્ય મિશ્રણ બનાવવા માટે ડ્રમ ની મહત્તમ ભ્રમણ ઝડપ કેટલી હોવી જોઈએ? (ડ્રમની ત્રિજ્યા $1.25\, m$ અને ધરી સમક્ષિતિજ ધારો)View Solution
- 8$1\, kg$ દળનો બ્લોક $\frac{1}{\sqrt{3}}$ સ્થિત ઘર્ષણાંક ધરાવતી સપાટી પર છે. બ્લોક પર $F\, N$ જેટલું લઘુતમ બળ લગાવતા તે ખસે છે. તો તો $F$નું મૂલ્ય નજીકના પૂર્ણાંકમાં કેટલું હશે? [$g =10 \,ms ^{-2}$ ]View Solution
- 9View Solutionવિધાન: વરસાદી દિવસો માં કાર કે બસ ચલાવવી મુશ્કેલ હોય છે.
કારણ: સપાટી ભીની થવાના લીધે ઘર્ષણાંક નું મૂલ્ય ઘટી જાય છે.
- 10$\theta $ જેટલો ઢોળાવ કોણ ધરાવતા એક ઢળતા સમતલનો ઉપરનો અડધો ભાગ સંપૂર્ણ લીસો છે, જયારે નીચેનો અડધો ભાગ ખરબચડો છે. સમતલના ઉપરના છેડેથી સ્થિર સ્થિતિમાંથી શરૂ કરીને જો એક બ્લોક પાટિયાના નીચેના છેડે ફરીથી સ્થિર સ્થિતિમાં આવે, જો આ બ્લોક અને સમતલના નીચેના અડધા ભાગનો ઘર્ષણાંક શેના વડે આપવામાં આવે?View Solution
