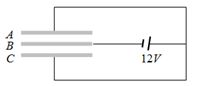
\(E = kQ\left[ {\frac{1}{{{1^2}}} + \frac{1}{{{2^2}}} + \frac{1}{{{4^2}}} + \frac{1}{{{8^2}}} + ...\infty } \right]\)
\(E = kQ\left[ {1 + \frac{1}{4} + \frac{1}{{16}} + \frac{1}{{64}} + ...\infty } \right]\)\(1 + \frac{1}{4} + \frac{1}{{16}} + \frac{1}{{64}} + ...\infty \)
\({S_\infty } = \frac{a}{{1 - r}}\) \(a = 1\) , \(r = \frac{1}{4}\) \(1 + \frac{1}{4} + \frac{1}{{16}} + \frac{1}{{64}} + .....\,\infty = \frac{1}{{1 - 1/4}} = \frac{4}{3}\)
\(E = 9 \times {10^9} \times Q \times \frac{4}{3} = 12 \times {10^9}\,Q\,N/C\)
\(V = \frac{1}{{4\pi {\varepsilon _0}}}\left[ {\frac{{1 \times {{10}^{ - 6}}}}{1} + \frac{{1 \times {{10}^{ - 6}}}}{2} + \frac{{1 \times {{10}^{ - 6}}}}{4} + \frac{{1 \times {{10}^{ - 6}}}}{8} + .......\infty } \right]\)
\( = \,9 \times {10^9} \times {10^{ - 6}}\left[ {1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + ............\infty } \right] = 9 \times {10^3}\left[ {\frac{1}{{1 - \frac{1}{2}}}} \right]\)
\( = 1.8 \times {10^4}\,volt\)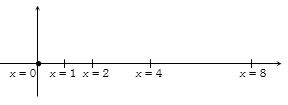
Download our appand get started for free
Similar Questions
- 1શુદ્ધ પાણીનો ડાય ઈલેકટ્રીક અચળાંક $81$ છે. તે પરમિટિવિટી ........ હશે.View Solution
- 2એક વિદ્યુત પરિપથમાં $1.0$ $kV$ વિદ્યુત વિભવની સામે $2$$\mu F$ કેપેસિટરોની જરૂર છે.$1$$\mu F$ ના ખૂબ જ મોટી સંખ્યામાં કેપેસિટરો છે,જે $300$ $V$ ના વિદ્યુત વિભવ કરતા વધુ વિદ્યૂત વિભવ સહિ શકતા નથી. તો આ માટે જરૂરી ઓછામાં ઓછા કેપેસિટરોની સંખ્યાView Solution
- 3બે સમાંતર ધાતુની પ્લેટની સમાન ધન ઘનતા $\left(\sigma=26.4 \times 10^{-12} C / m ^{2}\right)$ છે, તો બે પ્લેટ વચ્ચે વિદ્યુતક્ષેત્ર શોધો.View Solution
- 4સમાન કેપેસિટન્સ $C$ ધરાવતાં કેપેસિટરને $V_1$ અને $V_2$ વોલ્ટેજથી ચાર્જ કરીને સમાંતરમાં જોડતાં તે કેટલી ઊર્જા ગુમાવશે?View Solution
- 5બે અલગ કરેલી (અવાહકીય) પ્લેટોને સમાન રીતે એવી રીતે વિદ્યુતભારીત કરેલ છે. કે જેથી તેમની વચ્ચેનો સ્થિતિમાન તફાવત $V_2$ - $V_1$ = $20\ V$. પ્લેટ $2$ ઉંચા સ્થિતિમાન છે. પ્લેટોને $= 0.1\ m$ અંતરે અલગ કરેલી અનંત રીત વિશાળ (વિસ્તૃત) ગણી શકાય છે. પ્લેટ $1$ ની અંદરની પસાર પર સ્થિત સ્થિતિએ રહેલા એક ઈલેકટ્રોનને મુક્ત કરવામાં આવે છે. જે જ્યારે પ્લેટને અથડાય ત્યારે તેની ઝડપ કેટલી છે.View Solution
$ (e = 1.6 × 10^{-19}\ C, m_0= 9.11 × 10^{-31}\ kg)$
- 6$R $ ત્રિજયા ધરાવતા અને સમાન રીતે વિદ્યુતભાર ઘન ગોળાની સપાટી પર સ્થિતિમાન $V_0$ (અનંત ($\infty$)ની સરખામણીએ) છે.આ ગોળા માટે $\frac{{3{V_0}}}{2},\;\frac{{5{V_0}}}{4},\;\frac{{3{V_0}}}{4}$ અને $\frac{{{V_0}}}{4}$ સ્થિતિમાન ધરાવતી સમસ્થિતિમાન પૃષ્ઠ ( સપાટીઓ) ની ત્રિજયા અનુક્રમે $R_1,R_2,R_3$ અને $R_4$ છે, તો _________View Solution
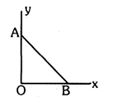
- 7આ આલેખ પરથીએક બિંદુવત વિદ્યુતભાર $+q$ ને ઉગમબિંદુ આગળ મૂકેલો છે. બીજા બિંદુવત વિદ્યુતભાર $-Q$ ને સુરેખ પથ $AB$ પર બિંદુ $A$ ના યામ $(0, a)$ ન થી બિંદુ $B$ ના યામ $(a, 0)$ ન સુધી લઈ જતાં થતુ કાર્ય ....... છે.View Solution
- 8$800$ માઈક્રો ફેરેડના કેપેસિટર પર $8 \times 10^{-18}\, C$ નો વિદ્યુતભાર મૂકવા કરવું પડતું કાર્ય ....View Solution
- 9$6\ cm$ ત્રિજયા ઘરાવતા ગોળીય કવચને સમકેન્દ્રિત રહે તેમ $4\ cm$ ત્રિજયા ઘરાવતો ગોળો મુકેલ છે. બહારની ગોળીય કવચને ગ્રાઉન્ડ કરેલી છે.જો અંદરના ગોળાનો વોલ્ટેજ $3\ e.s.u$ હોય તો તેમાં વિદ્યુતભાર કેટલા .......$ e.s.u.$ થાય?View Solution
- 10ત્રણ પ્લેટો $A, B, C$ દરેક $50\, cm^2$ નું ક્ષેત્રફળ ધરાવે છે તથા તેમની વચ્ચેનું અંતર $3\ mm$ છે તો જ્યારે પ્લેટ પૂરી વિદ્યુતભારીત થાય ત્યારે તેમાં સંગ્રહાયેલ ઊર્જા....View Solution