યંગના ડબલ-સ્લિટ પ્રયોગમાં પડદા પરના જે બિંદુએ પથ તફાવત $\lambda $ છે, ત્યાં પ્રકાશની તીવ્રતા $K$ જેટલી છે,$(\lambda$ વપરાયેલ પ્રકાશની તરંગલંબાઇ છે). જે બિંદુએ પથ તફાવત $\frac{\lambda }{4}$ હોય ત્યાં તીવ્રતા કેટલી થાય?
AIPMT 2014, Medium
b
Intensity at any point on the screen is
Intensity at any point on the screen is
\(I=4 I_{0} \cos ^{2} \frac{\phi}{2}\)
where \(I_{0}\) is the intensity of either wave and \(\phi\) is the phase difference between two waves.
Phase difference, \(\phi=\frac{2 \pi}{\lambda} \times\) Path difference When path difference is \(\lambda,\) then
\(\phi=\frac{2 \pi}{\lambda} \times \lambda=2 \pi\)
\(\therefore \,\,I = 4{I_0}{\cos ^2}\left( {\frac{{2\pi }}{2}} \right)\) \( = 4{I_0}{\cos ^2}(\pi )\) \( = 4{I_0} = K\) ....... \((i)\)
When path difference is \(\frac{\lambda}{4},\) then
\(\phi = \frac{{2\pi }}{\lambda } \times \frac{\lambda }{4} = \frac{\pi }{2}\)
\(\therefore \,\,{\text{ }}I = 4{I_0}{\cos ^2}\left( {\frac{\pi }{4}} \right)\) \( = 2{I_0} = \frac{K}{2}\) [using \((i)\)]
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionવિદ્યુતચુંબકીય તરંગો લંબગત હોવાની સાબિતી ......આપે છે.
- 2View Solutionકેવા ઉદ્ગમમાંથી ઉત્સર્જાતા તરંગો સુસબંદ્વ હોય ?
- 3યંગના બે સ્લિટના પ્રયોગમાં સોડિયમ લાઈટ સાથે સ્લીટની પહોળાઈ $0.589\, m$ છે. તો તૃતીય મહત્તમ અને કેન્દ્રીય મહત્તમ વચ્ચેનું કોણીય અંતર .....$( \lambda = \,589 \,nm)$View Solution
- 4પ્રકાશનો એક કિરણ જેમાં બે તરંગલંબાઇ $7000\; \mathring A$ અને $5500 \;\mathring A$ નો ઉપયોગ યંગના ડબલ સ્લિટ પ્રયોગમાં વ્યતિકરણની ભાત મેળવવા માટે થાય છે. સ્લિટ્સ વચ્ચેનું અંતર $2.5\,mm$ છે અને સ્લિટ્સના સમતલ અને પડદા વચ્ચેનું અંતર $150\,cm$ છે. મધ્યમાન શલાકાથી ઓછામાં ઓછું અંતર, જ્યાં બંને તરંગલંબાઇને કારણે તેજસ્વી શલાકા સંપાત થાય, તે $n \times 10^{-5}\,m$ છે. $n$ નું મૂલ્ય ............ છે.View Solution
- 5$200\, cm$ જેટલો ઓબ્જેક્ટિવ લેન્સનો વ્યાસ ધરાવતા ટેલિસ્કોપને $500\, nm$ તરંગ લંબાઈ ધરાવતા પ્રકાશના તરંગને પારખવા તેની વિભેદન ક્ષમતા કેટલી હોવી જોઈએ?View Solution
- 6View Solutionશ્વેત પ્રકાશ વ્યતિકરણમાં, કેન્દ્રની સૌથી નજીકની પ્રકાશિત શલાકાનો રંગ ક્યો હશે?
- 7યંગના ડબલ સ્લીટના પ્રયોગમાં શલાકાની જાડાઈનો ગુણોત્તર $4 : 1$ છે.પડદા પર મધ્યસ્થ અધિકત્તમની નજીક મહત્તમ અને ન્યુનત્તમ તીવ્રતાનો ગુણોત્તર કેટલો થાય?View Solution
- 8$50\,cm$ પહોળાઈ ધરાવતી નદીના કિનારા પર બહુમાળી ઈમાતરત છે દીવાદાંડીના ટાવરની ઊંચાઈ $40\,m$ છે $10\,m$ ઊંચાઈથી માણસને દીવાદાંડી નો પ્રકાશ પાણીની સપાટીથી ધ્રુવીભૂત થઈને દેખાય છે તે ઇમારતથી $x$ અંતરે થી આવતો પ્રકાશની તીવ્રતા લઘુતમ છે તે દીવાદાંડી પર રહેલા $y$ ઊંચાઈના બ્લબમાંથી આવતા પ્રકાશની તીવ્રતા બરાબર છે તો $x$ અને $y$ ના મૂલ્યો (પાણીનો વક્રીભવનાંક $ \simeq \frac{4}{3})$) છે.View Solution
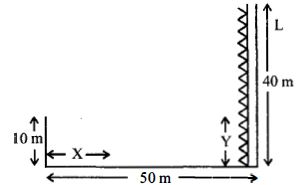
- 9$0.1\, \mu m$ પહોળાઈ ધરાવતાં છિદ્ર (પીન હોલ) પર સૂર્ય પ્રકાશ આપાત કરતાં મળતી વિવર્તન ભાત ધ્યાનમાં લો. જે છિદ્રનો વ્યાસ થોડોક વધારીએ તો વિવર્તન ભાત પર એવી રીતે અસર થશે કે ....... .View Solution
- 10પ્રકાશ કાચની પ્લેટ ($\mu$ = $1.5$) પર એવી રીતે આપાત થાય છે કે જેથી વક્રીભવન ખૂણો $60^o$ બને. કાળો પટ્ટો $ 6000 \,Å $ તરંગલંબાઈને અનુલક્ષીને અનુભવવામાં આવે છે. જો કાચની પ્લેટની જાડાઈ $1.2 \times\, 10^{-3 }\,mm$ હોય તો વ્યતિકરણ પટ્ટાનો ક્રમ શોધો.View Solution
