Question Bank
Explore our large set of questions to practice for your standard seamlessly- 1નીચેની માહિતીમાંથી $1.8\,^oC$ એ $Ca(OH)_2$$_{(s)}$ ની નિર્માણ ઉષ્મા ......$K\,cal.$View Solution
$CaO_{(s)}\,\, + \,\,{H_2}O_{(l)}\,\, \to \,\,Ca{(OH)_2}_{(s)}\,;\,\,\,........(i)$ $\,\Delta {H_{1.8\,^oC}} = \,\, - \,\,15.26\,\,K\,cal$
$H_2O_{(l)}\,$ $ \to $ ${H_{2{(g)}}}$ $+$ $\frac{1}{2}O_{2(g)}$ $\,\Delta {H_{1.8\,^oC}} = \,\, - \,\,68.37\,\,K\,cal$
$Ca_{(s)} + \frac{1}{2}O_{2(g)} = CaO_{(s)}$ $\,\Delta {H_{1.8\,^oC}} = \,\, \,\,-151.80\,\,K\,cal$
- 2પાણીના ઉત્કલન બિંદુએ $900\,J/g$ ઉષ્માનો વિનિમય થાય છે. તો એન્ટ્રોપીમાં થતો વધારો કેટલા ......$J/K-mole$ ?View Solution
- 3પાણીના બાષ્પાયન માટે $1$ વાતા દબાણે પ્રવાહી પાણી અને પાણીની બાષ્પમાં સંતુલન હોય ત્યારે તાપમાનનું મૂલ્ય કેટલા....$K$ થશે ?View Solution
$H_2O$ $_{(l)}$ $\rightleftharpoons$ $H_2O$ $_{(g)}$ [$1$ વાતા દબાણે] $[ \Delta S = 120 \,JK^{-1}$ અને $\Delta H = +45.0\, KJ ]$
- 4પાણીની બાષ્પ આદર્શ વાયુ છે. જ્યારે $1$ બાર દબાણ અને $100\,^{o}C$, એ $1$ મોલ પાણીનું બાષ્પીભવન થાય તો આંતરિક ઉર્જા ફેરફાર ($\Delta U$) શોધો. ($1$ બાર અને $373\,K$ પાણીની મોલર બાષ્પાયન એન્થાલ્પી $= 41\, kJ$ મોલ$^{-1}$ અને $R = 8.3 \,J$ મોલ$^{-1}$ $K$$^{-1}$)View Solution
- 5પાણીમાં $NaO{H_{\left( s \right)}}$ ની દ્રાવણ ઉષ્મા $ - 41.6\,kJ\,mo{l^{ - 1}}$ છે. જ્યારે $NaO{H_{\left( s \right)}}$ ને પાણીમાં દ્રાવ્ય કરવામાં આવે ત્યારે પાણીનું તાપમાન ..........View Solution
- 6પાણીમાં એક મોલ નિર્જળ $AB$ ક્ષારને દ્રાવ્ય કરતાં $21.0 \,J\, mol ^{-1}$ ઉષ્મા છૂટી પડે છે. $AB$ ના $\Delta H$ હાઈડ્રેશનનું મૂલ્ય $-29.4\, J\, mol ^{-1}$ છે. તો $AB.2H_2O$ $_{(s)}$ ક્ષારની હાઈડ્રેટેડ દ્રાવ્યની ઉષ્મા કેટલા .....$J\, mol ^{-1}$ ?View Solution
- 7View Solutionપુરોગામી પ્રક્રિયા આપમેળે થાય તે માટે જરૂરી શરત ...... છે.
- 8પ્રકિયા $2{C_{\left( {graphite} \right)}} + 2{H_{2\left( g \right)}} \to {C_2}{H_{4\left( g \right)}}$ માટે એન્થાલ્પી ફેરફાર......$kJ$ ગણો.View Solution
${C_{\left( {graphite} \right)}} + {O_{2\left( g \right)}} \to C{O_{2\left( g \right)}}\,;\,\Delta H = -393.5\,kJ$
${C_2}{H_{4\left( g \right)}} + 3{O_{2\left( g \right)}} \to 2C{O_{2\left( g \right)}} + 2{H_2}{O_{\left( l \right)}}\,;\,\Delta H = - 1410.9\,kJ$
${H_{2\left( g \right)}} + 1/2{O_{2\left( g \right)}} \to {H_2}{O_{\left( l \right)}}\,;\,\Delta H = - 285.8\,kJ$
- 9પ્રક્રિયા $2{H_{2\left( g \right)}} + {O_{2\left( g \right)}} \to 2{H_2}{O_{\left( l \right)}}$ માટે $\Delta H = - 571\,kJ$ છે. જો $H - H$ બંધઊર્જા $435\,kJ\,mo{l^{ - 1}}$ અને $O = O$ બંધઊર્જા $498\,kJ\,mo{l^{ - 1}}$ હોય, તો $O - H$ બંધની સરેરાશ ઊર્જા.....$kJ\,mo{l^{ - 1}}$ ગણો.View Solution
- 10પ્રક્રિયા $A \to B$ માટે $\Delta H = 4\,kcal\,mo{l^{ - 1}}$ અને $\Delta S = 10\,cal\,{K^{ - 1}}\,mo{l^{ - 1}}$ હોય, તો પ્રક્યિા .......$K$ તાપમાને સ્વયંભૂ હોઇ શકે ?View Solution
- 11પ્રક્રિયા $Cu_{\left( g \right)}^ + + I_{\left( g \right)}^ - \to Cu{I_{\left( s \right)}}$ માટે $\Delta {H^o}$ નું મૂલ્ય $ - 446\,kJ\,mo{l^{ - 1}}$ છે. જો $C{u_{\left( g \right)}}$ ની આયનીકરણ ઊર્જા $ 745\,kJ\,mo{l^{ - 1}}$ હોય અને ${I_{\left( g \right)}}$ ની ઇલેક્ટ્રોન બંધુતા $ -295\,kJ\,mo{l^{ - 1}}$ હોય, તો $C{u_{\left( g \right)}}$ અને ${I_{\left( g \right)}}$ માંથી $Cu{I_{\left( s \right)}}$ ના સર્જન માટે $\Delta {H^o}$ નુ મૂલ્ય.......$kJ$ જણાવો.View Solution
- 12પ્રક્રિયા $(i) \,{H_2}_(g)\,\, + \,\,C{l_2}(g)\,\, \to \,\,2HCl(g)\,\, + \,\,x\,KJ\,\,\,\,$View Solution
$(ii)\,{H_2}(g)\,\, + \,\,C{l_2}(g)\,\, \to \,\,2HCl(\ell )\,\, + \,\,y\,KJ$ માટે નીચેનામાંથી કયુ વિધાન સાચુ છે ?
- 13View Solutionપ્રક્રિયા આપમેળે થતી ન હોય, તો ...... વિકલ્પ સાચો છે.
- 14પ્રક્રિયાની ઉષ્મા નીચે પ્રમાણે છે : તો પ્રક્રિયા $C_2H_2$ + $H_2$ $\rightarrow$ $C_2H_4$ માટે ઉષ્મા ફેરફાર......$ K\, cal$View Solution
$(i)\,\,\Delta H_f^o\,\,of\,{H_2}{O_{(\ell )}}\, = \,\, - 68.3\,K\,\,cal\,\,mo{l^{ - 1}}$
$(ii)\,\,\Delta H_{comb}^o\,\,of\,{C_2}{H_2}\, = \,\, - 337.2\,K\,\,cal\,\,mo{l^{ - 1}}$
$(iii)\,\,\Delta H_{comb}^o\,\,of\,\,{C_2}{H_4}\,\, = \,\, - \,363.7\,\,K\,\,cal\,\,mo{l^{ - 1}} $
- 15પ્રક્રિયાની એન્થાલ્પીનો ઉપયોગ કરી $H_2O_2$$_{(l)}$ ના નિર્માણની એન્થાલ્પી......$kJ/mol$ માં શોધો.View Solution
$(i)$ $N_2H_4$$_{(l)}$ $+$ $2H_2O_2$$_{(l)}$ $\rightarrow$ $N_2$$_{(g)}$ $+$ $4H_2O$$_{(l)}$; $\Delta r{H_1}^ \circ = - 818 \,kJ/mol$
$(ii)$ $N_2H_4$$_{(l)}$ $+$ $O_2$$_{(g)}$ $\rightarrow$ $N_2$$_{(g)}$ $+$ $2H_2O$$_{(l)}$; $\Delta r{H_2}^ \circ = - 622 \,kJ/mol$
$(iii)$ ${H_2}_{(g)}\,\, $+$ \,\,\frac{1}{2}\,{O_2}_{(g)}\,\, \to \,\,{H_2}O_{(l)}\,\,\,;\,\,{\Delta }r{H_3}^ \circ \, = \,\, - 285\,\,kJ/mol$
- 16પ્રક્રિયામાં એન્થાલ્પી ફેરફાર ....... તરીકે ઓળખાય છે.View Solution
$2CO_{(g)} + O_{2{(g)}}$ $\rightarrow$ $2CO_{2{(g)}}$
- 17પ્રક્રિયા માટેનું $\Delta H^o\,\, -352.8\, kJ$ છે તો $F_2 + 2HCl$ $\rightarrow$ $2HF + Cl_2$ જો $HF$ માટે $\Delta H_f^o\,\, -268.3 \,kJ$ મોલ$^{-1}$ હોય તો $HCl$ ની $\Delta H_f^o$........$kJ$ મોલ$^{-1}$ થશે.View Solution
- 18પ્રતિમોલ ઈથેનોલની બાષ્પાયન એન્થાલ્પી કેટલા ............ $\mathrm{kJ/mol}$ થશે ? $(b.p. = 79.5\,^oC$ અને $\Delta S$ $= 109.8 $ $JK^{-1}\, mol^{-1}$) છે.View Solution
- 19પ્રતિવર્તીં પ્રક્રિયા માટે $T = 300\,K,$ કદ વધીને $V_f = 1\,L$ થી$ V_f = 10\,L$ થાય છે. તો જો પ્રક્રિયા સમઉષ્મીય હોય તો $\Delta H$ ................. $\mathrm{kJ}$ શોધો.View Solution
- 20પ્રબળ એસિડ અને પ્રબળ બેઈઝના તટસ્થીકરણથી પ્રતિ મોલ $H^+$ આયનોએ ઉદભવતી ઉષ્મા એ ...... હોય છે.View Solution
- 21View Solutionપ્રમાણિત મુક્ત ઊર્જા ફેરફાર અને સંતુલન અચળાંક વચ્ચેનો યોગ્ય સંબંધ ...... છે.
- 22View Solutionપ્રવાહીનું બાષ્પીભવન માટેની પ્રક્રિયા ....... થઈ પૂર્ણ થાય છે.
- 23પ્રાણાલી દ્વારા થતું કાર્ય $8\,J$ છે. જ્યારે $40\,J$ ઉષ્મા પસાર કરવામાં આવે ત્યારે પ્રક્રિયા દરમ્યાન પ્રાણાલીની આંતરિક ઉર્જામાં થતો ફેરફાર......$J$View Solution
- 24પ્રાણાલીની આંતરિક ઉર્જા $U_1$ છે, તો બહારથી $450\, J$ ઉષ્મા લે છે અને $600\, J$ કાર્ય પુરૂ કરે છે તો પ્રાણાલીની અંતિમ ઉર્જા .......View Solution
- 25બંધ પાત્રમાં $2$ મોલ કાર્બન મોનોકસાઈડ અને એક મોલ ઓક્સિજનનું મિશ્રણ પ્રજવલિત થઈને કાર્બન ડાયોકસાઈડ મળે છે. જો $\Delta H$ એન્થાલ્પી ફેરફાર અને $\Delta U$ એ આંતરિક ઉર્જામાં ફેરફાર થાય તો.....View Solution
- 26બે ઈલેકટ્રોનના ફેરફારને સમાવતી કોષ -પ્રક્રિયાનો પ્રમાણિત કોષ પોટેન્શિયલ $25^{0} C$ તાપમાને $0.295V$ છે. તો તેનો $25°C$ તાપમાને સંતુલન અચળાંક કેટલો થાય?View Solution
- 27બેન્ઝિનની દહન પ્રક્રિયા દરમિયાન થતો એન્થાલ્પી ફેરફાર$ = -3264.6$ કિલોજૂલ/મોલ હોય, તો $39$ ગ્રામ બેન્ઝિનના દહનથી ઉદભવતી ઉષ્મા ...... કિલોજૂલ હોય.View Solution
- 28બોમ્બ કેલેરીમીટરમાં એક મોલ ઝીંક રજ સાથે એક મોલ સલ્ફયુરીક એસિડની ઉષ્માક્ષેપક પ્રક્રિયા માટે $\Delta U$ અને $w$ નો સંબંધ .....View Solution
- 29મંદ $NaOH$ દ્રાવણ દ્વારા $1\,M\, HCl$ અને $1\, M\, H_2SO_4$ નાં સમાન કદનું તટસ્થીકરણ થાય છે અને $x$ અને $y \,K $ કેલરી ઉષ્મા અનુક્રમે છૂટી પડે છે. નીચેનામાંથી કયુ સાચું છે ?View Solution
- 30મિથેનના દહનનું $\Delta U^{\theta}$ મૂલ્ય $-X \,kJ \,mol ^{-1}$ છે. $\Delta H^{\theta}$ નું મૂલ્ય શું હશે ?View Solution
- 31મિથેનની દહનઉષ્મા $- 809\, kJ\, mol^{-1}$ છે. તો મિથેનનુ કેલરીમૂલ્ય કેટલા ....$kJ\,mo{l^{ - 1}}$ થશે ?View Solution
- 32રહોમ્બિક અને મોનોક્લિનિક સલ્ફરની દહન એન્થાલ્પી અનુક્રમે $70,960 $ અને $71,030$ કેલરી છે, તો રહોમ્બિક સલ્ફરના મોનોક્લિનિક સલ્ફરમાં થતાં રૂપાંતરણની એન્થાલ્પી ...... કેલરી થાય.View Solution
- 33વાયુમય પ્રક્રિયા માટે $A_{(g)} + 3B_{(g)} \rightarrow 3C_{(g)} + 3D_{(g)}$ $27\,^oC$ એ $\Delta U=17 \,Kcal$ છે. ધારો કે $R = 2 \,cal \,K$$^{-1}$ મોલ$^{-1}$ છે તો ઉપરની પ્રક્રિયા માટે $\Delta H$ નું મુલ્ય .......$Kcal$ થશે.View Solution
- 34View Solutionવિધાન : સંતુલને દરેક રાસાયણિક પ્રક્રિયા માટેનો પ્રક્રિયાનો પ્રમાણિત ગીબ્સ ઉર્જા ફેરફાર શૂન્ય થાય છે.
કારણ : અચળ તાપમાન અને દબાણે રાસાયણિક પ્રક્રિયા ગીબ્સ ઉર્જાના ઘટાડાની દિશામાં સ્વયંભુ થાય છે.
- 35વ્યક્તિ રોજ $640\,g \,\,O_2$ શ્વાસમાં લે છે. જો બધો જ $O_2$ શર્કરાનું $CO_2$ અને $H_2O$ માં રૂપાંતર માટે વપરાતો હોય તો કેટલો સુક્રોઝ ($C_{12}H_{22}O_{11}$) એક દિવસમાં શરીરમાં વપરાશે અને કેટલા .....$kJ$ ઉષ્મા ઉત્પન્ન] થાય છે ? $\Delta _{Hcombustion\, of\, sucrose}= -5645\, kJ\, mol^{-1}$.View Solution
- 36સમાન કદ ધરાવતા મોલર હાઇડ્રોક્લોરિક એસિડ અને સલ્ફયુરિક એસિડનું તટસ્થીકરણ મંદ $NaOH $ ના દ્રાવણ વડે કરતાં અનુક્રમે $x$ $KCal$ અને $y$ $KCal$ ઉષ્મા ઉત્પન્ન થાય છે. તો નીચેના પૈકી કયું સાચું છે ?View Solution
- 37સમીકરણના આધારે $1 $ લીટર કદના પાત્રમાં $2$ મોલ $CO$ અને $1$ મોલ $O_2$ લેવામાં આવે છે. જે નીચેના સમીકરણ દ્વારા $2$ મોલ $CO_2$ બનાવે છે.View Solution
$2CO + O_2 \rightarrow 2CO_2, \Delta H = - 560\,KJ.$ (આદર્શ સ્વરૂપમાંથી વાયુનું વિચલન થાય છે.$1\, atm - litre = 0.1\, KJ$)આ પ્રક્રિયા માટે, દબાણમાં $70\, atm $ થી $40\, atm$ ફેરફાર થાય છે. તો $500\, K$ એ $\Delta$$U$ નું મૂલ્ય ......$KJ$ શોધો.
- 38સમીકરણોની મદદથી $x$ ની $\to$ કિંમત......કિલોજૂલ માં શોધો :View Solution
${H_2}{O_{(g)}} + {C_{(s)}}\, \to \,\,C{O_{(g)}} + {H_{2(g)}}\,:\,\,\Delta H\, = \,\,131$ કિલોજૂલ $C{O_{(g)}} + \,\,\frac{1}{2}\,\,{O_{2(g)}} \to \,\,C{O_{2(g)}}\,:\,\,\Delta H\,\, = \,\, - 282$ કિલોજૂલ
${H_{2(g)}} + \frac{1}{2}{O_{2(g)}} \to \,{H_2}{O_{(g)}}\,:\,\Delta H\,\, = \,\, - 242\,\,$ કિલોજૂલ
$C_{(g)} + O_2$$_{(g)}$ $\to$ $CO_2$$_{(g)}$ : $\Delta H = x$ કિલોજૂલ
- 39View Solutionસમોષ્મી પ્રક્રિયા હેઠળ પ્રાણાલીનું વિસ્તરણ થાય ત્યારે.....
- 40View Solutionસમોષ્મી પ્રતિવર્તીં પ્રક્રિયા કે જે ....... એક છે.
- 41સાયક્લોહેકઝેન $(C_6H_{12})$,સાયક્લોહેકઝીન $(C_6H_{10})$, અને $H_2$ ની દહન એન્થાલ્પી અનુક્રમે $-3920, -3800$ અને $-241\, KJ\, mol$$^{-1}$ છે. તો સાયક્લોહેકઝીનની હાઈડ્રોજીનેશન ઉષ્મા ......$KJ \,mol ^{-1}$ થશે.View Solution
- 42સિલિન્ડરમાં $1$ વાતા. અચળ દબાણે $1.2$ લીટર $O_2$ વાયુમાં $1.0$ કિલો કેલરી ઉષ્મા ઉમેરવામાં આવે છે અને કદમાં $1.5$ લીટર ફેરફાર થાય છે. તો આ પ્રક્રિયામાં થતો આંતરિક ઊર્જાનો ફેરફારની ગણતરી ..... થશે.View Solution
- 43View Solutionસ્વયંભુ અપ્રતિવર્તીં પ્રક્રિયામાં પ્રાણીલી અને વાતાવરણની કુલ એન્ટ્રોપીમાં શું થાય ?
- 44સ્વીમીંગ પૂલમાંથી આવતો એક વ્યક્તિ તેના શરીર પર $30\, g$ પાણી ધરાવે છે. તો આ પાણીના બાષ્પીભવન માટે કેટલા .....$kJ$ ઉષ્મા જોઇએ ? (પાણીની બાષ્પાયન ગુપ્ત ઉષ્મા $40.79\, kJ/mol$ છે)View Solution
- 45હાઇડ્રેઝિન અને પાણીની પ્રમાણિત સર્જન-એન્થાલ્પી અનુકમે $+ 50.6\, kJ/mol$ અને $-285.9\, kJ/mol$ હોય તો નીચેની પ્રક્રિયા માટે $\Delta H$ જણાવો. ${N_2}{H_{4\left( g \right)}} + {O_{2\left( g \right)}} \to {N_{2\left( g \right)}} + 2{H_2}{O_{\left( l \right)}}$ .....$kJ\,mo{l^{ - 1}}$View Solution
- 46હિરો અને ગ્રેફાઈટની દહન એન્થાલ્પી અનુક્રમે $-395.4\, KJ$ અને $-393.5\,KJ$ છે. હિરામાંથી ગ્રેફાઈટના રૂપાંતરણની એન્થાલ્પી .....$KJ$ થશે.View Solution
- 47View Solutionહેસના ઉષ્માસંકલનના નિયમની મદદથી ...... એન્થાલ્પી જાણી શકાય છે.
- 48View Solutionહેસના નિયમ મુજબ પ્રક્રિયા ઉષ્માનો આધાર શેની પર રહેલો છે ?
- 49$100^{\circ} \mathrm{C}$ અને $1$ bar પર પાણી માટે $\Delta$બાષ્પ$\mathrm{H}^{\ominus}$ એ $+40.79 \mathrm{~kJ} \mathrm{~mol}^{-1}$ છે. સમાન પરિસ્થિતિ (તેજ પરિસ્થિતિ) હેઠળ આ બાષ્પીકરણ માટે આંતરિક ઉર્જા માં ફેરફાર. . . . . . . .$\mathrm{kJ} \mathrm{mol}^{-1}$ છે. (પૂર્ણાંક માં જવાબ)View Solution
(આપેલ : $\mathrm{R}=8.3 \mathrm{JK}^{-1} \mathrm{~mol}^{-1}$ )
- 50$27^{\circ} \mathrm{C}$ પર અચળ કદે ધન બેન્ઝોઈક એસિડ ની દહનઉષ્મા $-321.30 \mathrm{~kJ}$ છે. અચળ દબાણ પર દહનઉષ્મા $(-321.30-x \mathrm{R}) \mathrm{kJ}$ છે. $x$ નું મૂલ્ય ......... છે.View Solution
- 51$298 \mathrm{~K}$, પર પ્રકિયા $2 \mathrm{~A}+\mathrm{B} \rightarrow \mathrm{C}$ માટે,$\Delta \mathrm{H}=400 \mathrm{~kJ} \mathrm{~mol}^{-1}$ અને $\Delta \mathrm{S}=0.2 \mathrm{~kJ} \mathrm{~mol}^{-1} \mathrm{~K}^{-1}$ છે. ............. $K$ થી ઉપ૨ પ્રક્રિયા સ્વયંભૂ (આપમેળે) થશે.View Solution
- 52$\mathrm{C}-\mathrm{H}, \mathrm{C}-\mathrm{C}, \mathrm{C}=\mathrm{C}, \mathrm{H}-\mathrm{H}$ ની બંધઊર્જાઓ અનુક્મે $414 \mathrm{~kJ}, 347 \mathrm{~kJ}, 615 \mathrm{~kJ}$ અને $435 \mathrm{~kJ}$ હોય ત્યારે, હાઈડ્રોજન ના ઉમેરણ વડે ઈથિલિનમાંથી ઈથેન $\left(\mathrm{C}_2 \mathrm{H}_6\right)$ ની સર્જન એન્થાલ્પી $-$ ......... $\mathrm{kJ}$ છે.View Solution
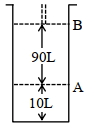
- 53આપેલ આક્રૂતિને ધ્યાનમાં લો.View Solution
$18^{\circ} \mathrm{C}$ પર, સ્થાન $A$ પર, પિસ્ટન સાથે જોડેલા (fitted) સિલિન્ડર માં આદર્શ વાયુનો $1$ $\mathrm{mol}$ રાખેલ છે. જો તાપમાન માં કોઈપણ જાતનો ફેરફાર ન કરીએ તો પિસ્ટન એ સ્થાન $B$ તરફ ખસે છે ત્યારે આ પ્રતિવર્તી પ્રક્રમ માં થયેલ કાર્ય $'x' L atm$ છે. $x=-$ ........... $L.atm$ (નજીક નો પૂર્ણાક)
[આપેલ : નિરપેક્ષ તાપમાન $={ }^{\circ} \mathrm{C}+273.15, \mathrm{R}=0.08206 \mathrm{~L} \mathrm{~atm} \mathrm{~mol}^{-1} \mathrm{~K}^{-1}$ ]
- 54એક આદર્શ વાયુ, $\overline{\mathrm{C}}_{\mathrm{v}}=\frac{5}{2}$ $R$. જ્યાં સુધી કદ બમણું ન થાય ત્યાં સુધી $1 \mathrm{~atm}$ ના અયળ દબાણ વિરુદ્ધ સમોષ્મી (રુધ્ધોષ્મી) વિસ્તરણ થાય છે. જો પ્રારંભિક તાપમાન અને દબાણ અનુક્રમે $298 \mathrm{~K}$ અને $5 \mathrm{~atm}$ હોય તો અંતિમ તાપમાન ........... $\mathrm{K}$ છે. (નજીકનો પૂર્ણાક)View Solution
[અચળ કદે મોલર ઉષ્માક્ષમતા $\bar{c}_{\mathrm{v}}$ છે]
- 55એક આદર્શ વાયુ ના ત્રણ moles ને $5$ atm ના અચળ દબાણ નો ઉપયોગ કરીને સમ તાપીય રીતે $60 \mathrm{~L}$ થી $20 \mathrm{~L}$ દબાવવામાં (સંકોચવામાં) આવ્યો. આ સંકોચન માટે ઉષ્મા વિનિયમ $Q$ એ - ............. Lit. atm છે.View Solution
- 56જ્યારે $1 \mathrm{M} \mathrm{HCl}$ અને $1 \mathrm{M} \mathrm{H}_2 \mathrm{SO}_4$ ના સમાન કદ ને $1 \mathrm{M} \mathrm{NaOH}$ દ્રાવણ ના વધુ કદ વડે (દ્વારા) અલગ અલગ રીતે તેનું તટસ્થીકરણ કરવામાં આવે છે ત્યારે અનુક્મે $x$ અને $y \mathrm{~kJ}$ ઉેષ્મા મૂકત થાય છે. $y / x$ નું મૂલ્ય. . . . . . . .View Solution
- 57જ્યારે $\Delta \mathrm{H}$ (બાષ્ય) $=30 \mathrm{~kJ} / \mathrm{mol}$ અને $\Delta \mathrm{S}$ (બાષ્ય) $=75 \mathrm{~J} \mathrm{~mol}^{-1} \mathrm{~K}^{-1}$, હોય ત્યારે એક વાતાવરણ પર બાષ્પનું તાપમાન. . . . . .$K$ છે.View Solution
- 58નિર્જળ $\mathrm{CuSO}_4$ અને $\mathrm{CuSO}_4 \cdot 5 \mathrm{H}_2 \mathrm{O}$ ના દ્રાવણ ની ઉષ્મા અનુક્રમે $-70 \mathrm{~kJ} \mathrm{~mol}^{-1}$ અને $+12 \mathrm{~kJ} \mathrm{~mol}^{-1}$ છે. $\mathrm{CuSO}_4$ થી $\mathrm{CuSO}_4 \cdot 5 \mathrm{H}_2 \mathrm{O}$ ની જલીયકરણ ની ઉષ્મા $-x \mathrm{~kJ}$ છે. તો $x$ નું મૂલ્ય. . . . . . . .છે. (નજીકનો પૂર્ણાક)View Solution
- 59નીચે બે વિધાનો આપેલા છે એક ને કથન ($A$) વડે લેબલ કરેલ છે બીજા ને કારણ ($R$) વડે લેબલ કરેલ છે.View Solution
કથન ($A$) : પ્રબળ મોનોબેઝિક એસિડ સાથે પ્રબળ મોનોએસિડિક બેઈઝ ની તટસ્થીકરણ એન્થાલ્પી હંમેશા $-57 \mathrm{~kJ} \mathrm{~mol}{ }^{-1}$ હોય છે.
કારણ ($R$) : જ્યારે એસિડ વડે અપાયેલ $\mathrm{H}^{+}$આયન ના એક મોલ એ બેઈઝ વડે અપાયેલ $\mathrm{OH}^{-}$આયનના એક મોલ સાથે જોડાઈ ને એક મોલ પાણી બનાવે છે ત્યારે ઊષ્માનો જથ્થો જે મુક્ત થાય છે તે તટસ્થીકરણ એન્થાલ્પી છે.
ઉપર્યુક્ત વિધાનોના સંદર્ભમાં, નીચે આપેલા વિકલ્પોમાંથી સાચો ઉત્તર પસંદ કરો.
- 60બેન્ઝિનના $1$ mole ના દહન ની અભિવ્યક્તિ કરેલ છે.View Solution
$\mathrm{C}_6 \mathrm{H}_6(1)+\frac{15}{2} \mathrm{O}_2(\mathrm{~g}) \rightarrow \mathrm{CO}_2(\mathrm{~g})+3 \mathrm{H}_2 \mathrm{O}(1) \text {. }$
બેન્ઝિનના $2 \mathrm{~mol}$ ની પ્રમાણિત દહન એન્થાલ્પી - ' $x^{\prime} \mathrm{kJ}$ છે. $x=$ ...........
આપેલ :
$(1)$ $6 \mathrm{C}($ ગ્રેફાઈટ $)+3 \mathrm{H}_2(\mathrm{~g}) \rightarrow \mathrm{C}_6 \mathrm{H}_6(\mathrm{l})$ પ્રકિયામાટે, $\mathrm{C}_6 \mathrm{H}_6(\mathrm{l})$, ના $1 \mathrm{~mol}$ ની પ્રમાણિત સર્જન એન્થાલ્પી $48.5 \mathrm{~kJ} \mathrm{~mol}^{-1}$ આપેલ છે.
$(2)$ $\mathrm{C}\left(\right.$ ગ્રેફાઈટ) $+\mathrm{O}_2(\mathrm{~g}) \rightarrow \mathrm{CO}_2(\mathrm{~g})$ પ્ર્ક્રિયામાટે, $\mathrm{CO}_2(\mathrm{~g})$ ના $1 \mathrm{~mol}$ ની પ્રમાણીત સર્જન એન્થાલ્પી $-393.5 \mathrm{~kJ}$ $\mathrm{mol}^{-1}$ છે.
$(3)$ $\mathrm{H}_2(\mathrm{~g})+\frac{1}{2} \mathrm{O}_2(\mathrm{~g}) \rightarrow \mathrm{H}_2 \mathrm{O}(\mathrm{l})$ is પ્રક્રિયા માટે, $\mathrm{H}_2 \mathrm{O}(\mathrm{l})$ ના $1 \mathrm{~mol}$ ની પ્રમાણીત સર્જન એન્થાલ્પી $-286 \mathrm{~kJ}$ $\mathrm{mol}^{-1}$ છે.
- 61$300 \mathrm{~K}$ પર જો એક આદર્શ વાયુ ના ત્રણ $moles$ $80 \mathrm\ {kPa}$ ના અચળ દબાણ વિરુધ્ધ સમતાપીય રીતે $30 \mathrm{dm}^3$ માંથી $45 \mathrm{dm}^3$ વિસ્તરણ પામતો હોય તો, સ્થાનાંતરણ પામતી ઉષ્માનો જથ્થો $\mathrm{J}$___________ છે.View Solution
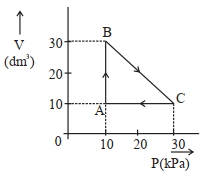
- 62$Image$ એક આદર્શ વાયુ બિંદુ $A$ થી શરૂઆત કરીને ચક્રિય સ્થાનાંતર કરે છે અને ઉપરની આકૃતિમાં દર્શાવ્યા પ્રમાણે દોરેલા પથ $\mathrm{A} \rightarrow \mathrm{B} \rightarrow \mathrm{C} \rightarrow \mathrm{A}$ દૃવારા તે જ બિંદુ પર પાછો ફરે છે. આ પ્રક્રમમાં થયેલ કુલ કાર્ય ____________$\mathrm{J}$ છે.View Solution
- 63$\mathrm{T}=400 \mathrm{~K}$ પર, એક નિશ્ચિત ઉષ્મારાસાયણિક પ્રક્રિયા $\mathrm{M} \rightarrow \mathrm{N}$ માટે, $\Delta H^{\ominus}=77.2 \mathrm{~kJ} \mathrm{~mol}^{-1}, \Delta \mathrm{S}=122$ $\mathrm{JK}^{-1}, \log$ સંતુલન અચળાંક $(\log \mathrm{K})$_______ $\times 10^{-1}$.છે.View Solution
- 64$\mathrm{CCl}_4$ માટે પ્રમાણુત બાષ્પાયન એન્થાલ્પી $30.5 \mathrm{~kJ}$ $\mathrm{mol}^{-1}$ છે. અચળ તાપમાન $284 \mathrm{~g} \mathrm{CCl}_4$ ના બાષ્પીકરણ માટે જરૂરી ઉષમા $\mathrm{kJ}$છે. (મોલર દળ $g$ mol ${ }^{-1}$ માં આપેલ છે. $\mathrm{C}=12, \mathrm{Cl}=35.5$ )View Solution
- 65જો $5$ મોલ આદર્શ વાયુ $300 \mathrm{~K}$ તાપમાને સમતાપી પ્રતિવર્તી પણે $10 \mathrm{~L}$ થી $100 \mathrm{~L}$ સુધી વિસ્તરણ પામે ત્યારે થતુ કાર્ય $-x$ $\times 10^1 \mathrm{~J} \mathrm{w}$, છે. તો $x$ જણાવો. $\left(\mathrm{R}=8.314 \mathrm{~J} \mathrm{~K}^{-1} \mathrm{~mol}^{-1}\right)$View Solution
- 66View Solutionનીચે આપેલામાંથી ક્યું સાચું નથી?
- 67View Solutionનીચે આપેલા માંથી સમોષ્મી પરિસ્થિતી હેઠળ એક આદર્શ વાયુના મુક્ત વિસ્તરણ માટે સાચો વિકલ્પ પસંદ કરો.
- 68નીચે બે પ્રક્રિયાઓ આપેલ છે.View Solution
$2 \mathrm{Fe}_{(\mathrm{s})}+\frac{3}{2} \mathrm{O}_{2(\mathrm{~g})} \rightarrow \mathrm{Fe}_2 \mathrm{O}_{3(\mathrm{~s})}, \Delta \mathrm{H}^{\mathrm{o}}=-822 \mathrm{~kJ} / \mathrm{mol}$
$\mathrm{C}_{(\mathrm{s})}+\frac{1}{2} \mathrm{O}_{2(\mathrm{~g})} \rightarrow \mathrm{CO}_{(\mathrm{g})}, \Delta \mathrm{H}^{\mathrm{o}}=-110 \mathrm{~kJ} / \mathrm{mol}$
$3\mathrm{C}_{(\mathrm{s})}+\mathrm{Fe}_2 \mathrm{O}_{3(\mathrm{~s})} \rightarrow 2 \mathrm{Fe}_{(\mathrm{s})}+3 \mathrm{CO}_{(\mathrm{g})}$ આપેલા પ્ર્ક્રિયા માટે એન્થાલ્પી ફેરફાર__ _ _$J/mol$ છે.
- 69$298\,K$ પર $A \rightleftharpoons B$ પ્રક્રિયા માટે $\log K$ નું મુલ્ય $.....$ છે.(નજીકનો પૂર્ણાક)View Solution
આપેલ : $\Delta H ^{\circ}=-54.07\,kJ\,mol ^{-1}$
$\Delta S ^{\circ}=10\,J\,K ^{-1}\,mol ^{-1}$
$(2.303 \times 8.314 \times 298=5705$ લો.)
- 70$2$ લીટર આદર્શ વાયુ શૂન્યાવકાશમાં સમતાપી રીતે જ્યાં સુધી કુલ કદ $6$ લીટર થાય ત્યાં સુધી વિસ્તરે છે, તો આંતરિક ઊર્જામાં થતો ફેરફાર $........$ છે.(નજીકનો પૂર્ણાક)View Solution
- 71$300\,K$ પર ઈથીનના સંપૂર્ણ દહન માટે ઉત્પન્ન થતી ઉષ્માના જથ્થાને બોમ્બ કેલોરીમીટર માં માપતા તે $1406\,kJ\,mol ^{-1}$ છે.$C _2 H _4( g )+3 O _2( g ) \rightarrow 2 CO _2( g )+2 H _2 O ( l )$ સંતુલને પહોંચવા માટે જરૂરી $T \Delta S$ નું ઓછામાં ઓછું મૂલ્ચ (ન્યૂનતમ મૂલ્ય) $(-).........\,kJ$.View Solution
(નજીકનો પૂર્ણાક) આપેલ : $R =8.3\,J\,K ^{-1}\,mol ^{-1}$
- 72$300\,K$ પર સ્વતંત્ર પ્રક્રમો માટે, સ્વયંભૂ ન થતી (આપમેળે ના થાય તેવી) પ્રક્રમોની સંખ્યા નીચે આપેલામાંથી $.........$ છે.View Solution
પ્રક્રમ $\Delta H / kJ\,mol ^{-1}$ $\Delta S / J K^{-1}$ $A$ $-25$ $-80$ $B$ $-22$ $40$ $C$ $25$ $-50$ $D$ $22$ $20$ - 73$350\,K$ પર આદર્શ વાયુ અને $4\,atm$ થર્મલ વાહક દિવાલોના $2.0\,L$ પાત્રમાં હોય છે, જે પર્યાવરણના સંપર્કમાં હોય છે.તે $4\,atm$ ના અચળ દબાણ વિરુદ્ધ સમતાપી પ્રતિવર્તી $........\,J\,K ^{-1}$ છે.(નજીકનો પૂર્ણાક) આપેલ : $R =8.314\,J\,K ^{-1}\,mol ^{-1}$.View Solution
- 74$CCl _{4( g )}, H _2 O ( g ), CO _{2( g )}$ અને $HCl ( g )$ ની સર્જન એેન્થાલ્પી અનુક્રમે $-105,-242,-394$ અને $-92\,kJ\,mol^{-1}$ છે.નીચે આપેલ પ્રક્રિયાની એન્થાલ્પીની માત્ર $..........\,kJ\,mol^{-1}$ (નજીકનો પૂર્ણાંક)View Solution
$CCl _{4( g )} + 2 H _2 O ( g ) \rightarrow CO _{2( g )} + 4 HCl ( g )$
- 75આપેલ,View Solution
$(A)$ $2 CO ( g )+ O _2( g ) \rightarrow 2 CO _2( g ) \quad \Delta H _1^\theta=- x\,kJ\,mol { }^{-1}$
$(B)$ $C$ (graphite) $+ O _2$ (g) $\rightarrow CO _2$ (g) $\Delta H _2^\theta=- y\,kJ\,mol -1$
$C$(ગ્રેફાઈટ) $+$ $\frac{1}{2} O _2( g ) \rightarrow CO ( g )$ પ્રક્રિયા માટે $\Delta H ^\theta$ શોધો.
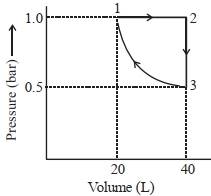
- 76એક મોલ આદર્શ એકપરમાણ્વીય વાયુને આલેખમાં દર્શાવ્યા પ્રમાણે ફેરફાર કરેલ છે. થયેલ કાર્યની માત્રા (પ્રણાલી વડે અથવા પ્રણાલી ઉપર) $..........J$ છે. (નજીકનો પૂર્ણાક) Given : $\log 2=0.3, \ln 10=2.3$View Solution
- 77એક મોલ સોડિયમ કલોરાઈડને પીગાળવા માટે $30.4\,kJ$ ઉષ્મા જરૂરી છે અને ગલનબિંદ્દ પર એન્ટ્રોપી ફેરફાર $1\,atm$ પર $28.4\,J\,K ^{-1} mol ^{-1}$ છે.તો સોડિયમ કલોરાઈડનું ગલનબિંદુ $.....\,K$ છે.(નજીકનો પૂર્ણાક)View Solution
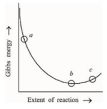
- 78ગિબ્સ મુક્ત ઊર્જા વિરુદ્ધ પ્રક્રિયા ની હદ (વ્યાપ)ના આલેખ ને ધ્યાનમાં લો.નીચે આપેલામાંથી વિધાનોની સંખ્યા બિંદુઓ $(a), (b)$ અને $(c)$ના સંદર્ભમાં સાચા છે તે $......$View Solution
$A$.$(a)$ અને $(b)$ પર પ્રક્રિયા સ્વંયભૂ (આપમેળે) છે.
$B$. પ્રક્રિયાબિંદુ $(b)$ પર સંતુલન પર છે અને બિંદુ $(c)$ પર સ્વંયભૂ (આપમેળે) નથી.
$C$. પ્રક્રિયા $(a)$ પર સ્વંયભૂ (આપમેળ) છે અને $(c)$ પર સ્વંયભૂ (આપમેળે) નથી.
$D$. પ્રક્રિયા $(a)$ અને $(b)$ પર સ્વંયભૂ (આપમેળે) નથી.
- 79જયારે $60\,W$ ઈલેકિટ્રક હીટર ને વાયુમાં $100\,s$ માટે સમોષ્મી દિવાલો સાથે સમોષ્મી સાથે ના અચળ કદ ના પાત્રમાં $100\,s$માટે ડુબાડવામાં આવે છે.ત્યારે વાયુ નું તાપમાન $5^{\circ}\,C$ વધે છે.આપેલ વાયુ ની ઉષ્માક્ષમતા $........\,J\,k ^{-1}$ છે.(નજીકનો પૂર્ણાક)View Solution
- 80જ્યારે મિથેન પ્રણાલી $A$ અને $B$ માં અનુક્રમે દહન થાય તો શું થાય છે ?View Solution
પ્રણાલી $A$ પ્રણાલી $B$ સમોષ્મી પ્રણાલી ડાયથર્મીક પાત્ર - 81નીચે આપેલામાંથી માત્રાત્મક ગુણધર્મો ધરાવતા હોય તેની કુલ સંખ્યા $.........$ છે. કદ, મોલર ઉષ્માક્ષમતા, મોલારીટી, $E ^{\varnothing}$ કોષ,ગિબ્ગીસ મુક્ત ઊર્જા ફેરફાર, મોલર દળ, મોલView Solution
- 82નીચેના માંથી ક્યાં સંબંધો સાચાં છે?View Solution
$(A)$ $\Delta U = q + p \Delta V$
$(B)$ $\Delta G =\Delta H - T \Delta S$
$(C)$ $\Delta S =\frac{ q _{ rev }}{ T }$
$(D)$ $\Delta H =\Delta U -\Delta nRT$
નીચે આપેલા વિકલ્પોમાંથી યોગ્ય ઉત્તર પસંદ કરો.
- 83પ્રમાણિત રિડક્ષન પોટેન્શિયલ $M ^{+} / M$ કે જે રિડ્યુસીંગ સામર્થ્ય (શક્તિ)નું માપ આપે છે, ના ઉપર નિર્ભર નથી તે $........$View Solution
- 84રોકેટમાં ઉપયોગમાં લેવાતું ધન બળતણ એ $Fe _2 O _3$ અને $Al$ નું એક મિશ્રણ $(1:2$ના ગુણોત્તરમા)છે.મિશ્રણના પ્રતિગ્રામ નીકળતી ઉષ્મા $(kJ).............$ છે.(નજીકનો પૂર્ણાક)View Solution
આપેલ : $\Delta H _{ f }{ }^\theta\left( Al _2 O _3\right)=-1700\,kJ\,mol ^{-1}$
$\Delta H _{ f }{ }^\theta\left( Fe _2 O _3\right)=-840\,kJ\,mol ^{-1}$
$Fe , Al$ અને $O$ નું મોલર દળ અનુક્રમે $56,27$ અને $16\,g\,mol ^{-1}$.
- 85View Solutionસોડીયમ હેલાઇડોની પ્રમાણિત સર્જન એન્થાલ્પી નો સાચો ક્રમ શોધો.
- 86$1\,mole$ આદર્શવાયુ ને પ્રતિવર્તીય અને સમોષ્મીય રીતે $27^{\circ}\,C$ તાપમાન થી વિસ્તરવા દેવામાં આવે છે. થયેલ કાર્ય $3\,kJ\,mol ^{-1}$ છે. વાયુનું અંતિમ તાપમાન $.........K$ છે. (નજીકનો પૂર્ણાંક) આપેલ : $CV _{ V }=20\,J\,mol ^{-1}\,K ^{-1}$View Solution
- 87$25^{\circ}\,C$ અને $1\,atm$ પર $16.8\,L$ વાયુમય મિશ્રણ ઈથીન અને મિથેન સંપૂર્ણ દહન કરતાં $CO _2$ ના $28.0\,L$ ઉત્પન્ન થાય છે. દહન પ્રકમ દરમ્યાન નીકળતી (ઉત્પન્ન) થતી ઉષ્મા $...........\,kJ$.આપેલ : $\Delta Hc \left( CH _4\right)=-900\,kJ\,mol ^{-1}$ $\Delta Hc \left( C _2 H _4\right)=-1400\,kJ\,mol ^{-1}$View Solution
- 88$27^{\circ}C$ પર બોમ્બ કેલોરીમીટરમાં $0.3\,g$ ઈથેનનું દહન થાય છે. કેલોરીમીટર પ્રણાલીનું તાપમાન (પાણીને ગણીને) $0.5^{\circ}C$ વધેલ મળી આવેલ છે. તો અચળ દબાણ પર ઈથેનના દહન દરમિયાન નિકળતી ઉષ્મા $......\,kJ\,mol^{-1}$.(નજીકનાં પૂર્ણાંકમાં)View Solution
[આપેલ : કેલોરીમીટર પ્રણાલીની ઉષ્માક્ષમતા $20\,kJ\,K^{-1}$ છે $R = 8.3\,JK^{-1}mol^{-1}$. આદર્શ વાયુ વર્તણૂંક ધારી લો.$C$ અને $H$ ના પરમાણ્વિય દળ અનુક્રમે $12$ અને $1\,g\,mol^{-1}$ છે.]
- 89$A _2+ B _2 \rightarrow 2 AB . \Delta H_f^0=-200\,kJ\,mol ^{-1} AB , A _2$ અને $B _2$ એ દ્રીપરમાણ્વિક અણુઓ છે. $A _2, B _2$ અને $AB$ બી બંંધ એન્થાલ્પીઓ $1:0.5:1$ના ગુણોત્તરમાં હોય તો, તો પછી $A _2$ ની બંંધ એન્થાલ્પી $.........\,kJ\,mol ^{-1}$ (નજીકનો પૂર્ણાક)View Solution
- 90$\frac{1}{2} Cl _2( g )$ માંથી $Cl ^{-}$(aq)ના પરિવર્તન માટે એન્થાલ્યી ફેરફાર $(-).......kJ\,mol { }^{-1}$ છે. (નજીકની પૂર્ણાંક)View Solution
આપેલ :$\Delta_{ dis } H _{ Cl _{2(g)}}^{\circ}=240\,kJ\,mol ^{-1}$.
$\Delta_{ eg } H _{ Cl _{(g)}}^{\circ}=-350\,kJ\,mol ^{-1}$,
$\Delta_{ hyd } H _{ Cl i _{( j )}^{\circ}}^{\circ}=-380\,kJ\,mol ^{-1}$
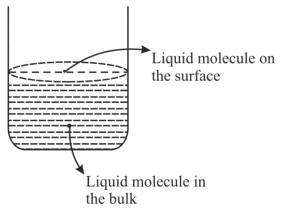
- 91આપેલ આકૃતિના આધારે, સાયા વિધાન/નો ની સંખ્યા $.........$ છે.View Solution
$A.$ જથ્થામાં (બલ્કમાં) પ્રવાહી અણુ પર આકર્ષણ અને અપાકર્ષણ બળો સમાન રીતે વર્તે ત્યારે પૃષ્ઠતાણનું નિર્માણ થાય છે.
$B.$ સપાટી ઉપર હાજર અણુઓ પર અસમાન બળો પ્રવર્તમાન $(uneven\,forces)$ના કારણે પૃષ્ઠતાણ છે.
$C.$ જથ્થામાં (બલ્કમાં) અણુ પ્રવાહી સપાટી (સ્તર) પર આવતાં નથી.
$D.$ જો પ્રણાલી એ બંધ પ્રણાલી હોય તો સપાટી ઉપરના અણુઓ એ બાષ્પદબાણ માટે જવાબદાર છે.
- 92એક રમતવીર $(athlete)$ ને ઉર્જા માટે $100\,g$ ગ્લુકોઝ $\left( C _6 H _{12} O _6\right)$ આપેલ છે. આ $1800\,J$ ઉર્જાને સમતુલ્ય છે. આ પ્રાપ્ત ઉર્જાના $50\%$ નો ઉપયોગ રમતવીર દ્વારા કાર્યકમ $(event)$ પર રમતગમતની પ્રવૃતિઓ માટે કરવામાં આવે છે. ઉર્જાના સંગ્રહને અવગણીએ તી પાણીનું વજન જેન તેને પરસેવો પાડવાની જરુર પડશે તે $.............g$ (નજીકનો પૂર્ણાક)View Solution
આપેલ : પાણીની બાષ્પીભવન એન્થાલ્પી $45\,kJ\,mol ^{-1}$
$C, H$ અને $O$ નું મોલર દળ $12,1$ અને $16\,g\,mol ^{-1}$.
- 93નીચે આપેલામાંથી ઉષ્માશોષક પ્રક્રમ(મો)ની સંખ્યા $.....$ છે.View Solution
$A.$ $I _2( g ) \rightarrow 2 I ( g )$
$B.$ $HCl ( g ) \rightarrow H ( g )+ Cl ( g )$
$C.$ $H _2 O ( l ) \rightarrow H _2 O ( g )$
$D.$ $C ( s )+ O _2( g ) \rightarrow CO _2( g )$
$E.$ પાણીમાં એમોનિયમ કલોરાઈડનું વિલયન (ઓગળવું)
- 94નીચેની પ્રક્રિયા કે જે $27^{\circ}\,C$ અને $1\,atm$ દબાણ પર સંતુલન પ્રસ્થાપિત કરે છે તેને ધ્યાનમાં લો.View Solution
$A + B \rightleftharpoons C+D$
$27^{\circ}\,C$ પર પ્રમાણિત મુક્ત ઊર્જા ફેરફાર $\left(\Delta_{ r } G ^0\right)$ $(-)$ $............kJ mol ^{-1}$ છે. (નજીકની પૂર્ણાંક)
(આપેલ : $R =8.3\,Jk ^{-1}\, mol ^{-1}$ અને In $10=2.3$ )
- 95$25^{\circ} C$ અને $1\,atm$ દબાણ પર બેન્ઝિન$_{(l)}$ અને એસિટિલીનની$_{(g)}$ દહન એન્થાલ્પી અનુક્રમે $-3268\,kJ\,mol$ ${ }^{-1}$ અને $-1300\,kJ\,mol ^{-1}$છે. પ્રક્રિયા માટે એન્થાલ્પી ફેરફાર શોધો.View Solution
$3 C _{2} {H _{2}}_{(g)} \rightarrow C _{6} {H _{6}}_{(l)}$, is $.....\,kJ \,mol ^{-1}$
- 96$25^{\circ} C$ અને $1$ વાતા દબાણે દહન એન્થાલ્પીનો નીયે આપેલ છે.View Solution
પદાર્થ $H _{2}$ $C$(ગ્રેફાઈટ) $C _{2} H _{6}( g )$ $\frac{\Delta_{ C } H ^{\Theta}}{ kJmol ^{-1}}$ $-286.0$ $-394.0$ $-1560.0$ તો,ઈથેનની સર્જન એન્થાલ્પી ........
- 97$298\,K$ પર $4 Fe ( s )+3 O _{2}( g ) \rightarrow 2 Fe _{2} O _{3}( s )$ પ્રક્રિયા માટે પ્રમાણિત એન્ટ્રોપી ફેરફાર $-550\,J / K$ છે. ક્યા તાપમાન $K$ પર પ્રક્રિયામાં સંતુલન સ્થપાશે ? [આપેલ; $\Delta H ^{\circ} r =-165\,kJ\,mol ^{-1}$.]View Solution
- 98$300 K$ અને $1 \,bar$ દબાણ પર એક મોલ મેગ્નેશિયમને ખૂલ્લા પાત્રમાં દહન માટે, $\Delta_{ C } H ^{\ominus}=-601.70 \,kJ\, mol^{-1}$, પ્રક્રિયા માટે આંતરિક ઉર્જા ફેરફારની માત્રા $kJ$ છે. (નજીકનો પૂર્ણાંક)View Solution
(આપેલ : $R =8.3\, J \,K ^{-1} \,\,mol ^{-1}$ )
- 99$-33.42^{\circ}\,C$ અને $1\,bar$ દબાણ પર $NH _{3}$ ના $17.0\,g$ સંપૂર્ણ બાષ્પીકરણ પામે છે અને આ પ્રક્રમમાં એન્થાલ્પી ફેરફાર $23.4\,kJ\,mol ^{-1}$ છે. સમાન પરિસ્થિતિઓ હેઠળ $85 g\,NH _{3}$ ના બાષ્પીકરણ માટે એન્થાલ્પી ફેરફાર $\dots\dots\dots\,\,kJ$ છે.View Solution
- 100$5$ મોલ હિલિયમ વાયુ, $300\, K$ તાપમાને, પ્રતિવર્તીય અને સમતાપીય વિસ્તરણ થઈ $10\, L$ થી $20 \,L$ થાય છે, આ દરમિયાન પ્રાપ્ત થયેલા મહત્તમ કાર્યની માત્રા ..........$J$ છે [નજીકની પૂર્ણાંક] (આપેલું છે$: R = 8.3 \,J \,K ^{-1}\, mol ^{-1}$ અને $\log 2=0.3010$ )View Solution