Question Bank
Explore our large set of questions to practice for your standard seamlessly- 1સાંદ્ર જલીય સલ્ફ્યુરીક એસિડ એ $ 98\% $ $H_2SO_4$ વજનથી ધરાવે અને ઘનતા $1.80 $ ગ્રામ મિલી$^{-1}$. $1$ લીટર $0.1\,M$ $H_2SO_4$ દ્રાવણ બનાવવા માટે એસિડનું ....... $mL$ કદ જરૂરી છે.View Solution
- 2સિલ્વર નાઈટ્રેટનો અવલોકીત અને ગણતરી કરેલ અણુભાર અનુક્રમે $92.64$ અને $170$ હોય છે. સિલ્વર-નાઈટ્રેટનો વિયોજન અંશ ........ $\%$ થાય.View Solution
- 3સુકોઝનું $ 5\%(w/v)$ દ્રાવણએ પદાર્થ $ 'A' $ ના $ 1\%(w/v) $ દ્રાવણ સાથે આઈસોટોનીક થાય છે. તો પદાર્થ $'A'$ નો અણુભાર કેટલો થાય?View Solution
- 4સૂકી હવાને સૌ પ્રથમ $10$ ગ્રામ દ્રાવ્ય અને $90 $ ગ્રામ પાણી ધરાવતા દ્રાવણ માથી અને ત્યારબાદ શુધ્ધ પાણીમાંથી પસાર કરવામાં આવે છે. દ્રાવણના વજનમાં $2.5 $ ગ્રામ અને દ્ર|વકના વજનમાં $0.05$ ગ્રામ ઘટાડો જણાય છે. તો દ્રવ્યનો અણુભાર……. થાય.View Solution
- 5View Solutionસોડિયમ ક્લૉરાઇડનું ......સાંદ્રતાવાળું દ્રાવણ મનુષ્યના રુધિરમાં આવેલા રક્તકણોના પ્રવાહી પ્રત્યે આઇસોટોનિક છે.
- 6$0.05 \mathrm{M} \mathrm{CuSO}_4$ ની જ્યારે$0.01 \mathrm{M} \mathrm{K}_2 \mathrm{Cr}_2 \mathrm{O}_7$ સાથે પ્રક્રિયા ક૨વામાં આવે છે જ્યારે $\mathrm{Cu}_2 \mathrm{Cr}_2 \mathrm{O}_7$ ના લીલા રંગનું દ્રાવણ આપે છે. બે દ્રાવણોને નીચે દર્શાવ્યા મુજબ અલગ પાડવામાં આવે છે.અભિસરણ (પરાસરણ) ના કારણે :View Solution
${K}_2 \mathrm{Cr}_2 \mathrm{O}_7$ & ${CuSO}_4$
SideX $SPM$ Side $\mathrm{Y}$ Due to osmosis :
- 7$100 \mathrm{~g}$ પાણીમાં $10 \mathrm{~g}$ વિદ્યુતવિભાજ્ય $\mathrm{AB}_2\left(\mathrm{AB}_2 \rightarrow \mathrm{A}^{2+}+2 \mathrm{~B}^{-}\right)$ધરાવતું એક દ્રાવણ $100.52^{\circ} \mathrm{C}$ એ ઉકળે છે. વિદ્યુતવિભાજ્યનો આયનીકરણ અંશ $(\alpha)$. ......... $\times 10^{-1}$છે.View Solution
[ $\mathrm{AB}_2$ નું મોલર દળ $=200 \mathrm{~g} \mathrm{~mol}{ }^{-1}$, પાણીનું ઉત્કલનબિંદુ $=100^{\circ} \mathrm{C}, \mathrm{K}_{\mathrm{b}}$ (પાણીનો મોલલ ઉત્કલનબિંદુ ઉન્નયન અચળાંક $\left.=0.52 \mathrm{~K} \mathrm{~kg} \mathrm{~mol}^{-1}\right)$ ]
- 8$25^{\circ} \mathrm{C}$ પર $100 \mathrm{~g}$ પાણીમાં $2.5 \mathrm{~g}$ બાષ્પશીલ, વિદ્યૃત-અવિભાજ્ય ને ઓગાળવામાં આવે છે. દ્રાવણ ઉત્કલન બિંદુમાં ઉન્નયન $2^{\circ} \mathrm{C}$ પ્ર્દ્શિત કરે છે. એવું ઘારી લો કે દ્રાવક સાંદ્રતા ના સંદર્ભમાં દ્રાવ્ય સાંદ્રતા જે ને અવગણવામાં આવે છે. પરિણામ જલીય દ્રાવણનું બાષ્પદબાણ ............ $\mathrm{mm} \mathrm{Hg}$ ના છે. (નજીક નો પૂર્ણાક)View Solution
[ આપેલ : પાણીનો મોલલ ઉત્કલનબિંદુ ઉન્નયન અચળાંક $\left(\mathrm{K}_{\mathrm{b}}\right)=0.52 \mathrm{~K} . \mathrm{kg} \mathrm{mol}^{-1}$,
$1 \mathrm{~atm}$ દબાણ $=760 \mathrm{~mm} \mathrm{Hg}$, પાણીનું મોલર દળ $\left.=18 \mathrm{~g} \mathrm{~mol}^{-1}\right]$
- 9$27^{\circ} \mathrm{C}$ પર શુદ્ધ બેન્ઝિન અને મિથાઈલ બેન્ઝિનનું બાષ્પદબાણ અનુક્રમે $80$ $Torr$ અને $24$ $Torr$ છે. સમાન તાપમાન પર બંન્ન પ્રવાહીઓનું (આદર્શ દ્રાવણ) એક સમમોલર મિશ્રણ સાથે સંતુલનમાં બાષ્પ અવસ્થામાં મિથાઈલ બેન્ઝિનના મોલઅંશ ........... (નજીકનો પૂર્ણાક) $\times 10^{-2}$ છે.View Solution
- 10અર્ધપારગમ્ય પડદા સાથેના કેખ્સ્યુલ માં રાખેલા $0.2 \mathrm{M}$ ગ્લુકોઝ ના દ્રાવણ વડે એક કૃત્રિમ કોષ તૈયાર કરવામાં આવ્યો. જ્યારે આ કૃત્રિમ કોષને $300 \mathrm{~K}$ પર $0.05 \mathrm{M} \mathrm{NaCl}$ ના દ્રાવણમાં મૂકવામાં આવે છે. ત્યારે અભિસરણ (પરાસરણ) દબાણ ઉત્તપન થાય છે.. ........ $\times 10^{-1}$ bar છે. (નજીકનો પૂર્ણાક )View Solution
[ આપેલ : $\mathrm{R}=0.083 \mathrm{~L} \mathrm{bar} \mathrm{mol}^{-1} \mathrm{~K}^{-1}$ ]
$\mathrm{NaCl}$ નું સંપૂર્ણ વિયોજન થાય છે તે ધારી લો.
- 11એસિટિક એસિડ નું પાણીમાં વિયોજન ધ્યાનમાં લઈએ તો, તો તેનો વિયોજન અચળાંક $6.25 \times 10^{-5}$ છે. જો $5 \mathrm{~mL}$ એસિટિક એસિડને $1 litre$ પાણીમાં ઓગાળવામાં આવે તો, દ્રાવણ $-x \times 10^{-2}{ }^{\circ} \mathrm{C}$ પર ઠરે છે. આપેલ શુધ્ધ પાણી $0^{\circ} \mathrm{C}$ પર ઠરે છે. $X=$ ..................... (નજીક નો પૂર્ણાક)View Solution
આપેલ : $\left(\mathrm{K}_{\mathrm{r}}\right)_{\text {water }}=1.86 \mathrm{~K} \mathrm{~kg} \mathrm{~mol}^{-1}$.
એસિટિક એસિડની ઘનતા $1.2 \mathrm{~g} \mathrm{moL}^{-1}$.
પાણી નું મોલર દળ $=18 \mathrm{~g} \mathrm{~mol}^{-1}$.
એસિટિક એસિડ નું મોલર દળ = $60 \mathrm{~g} \mathrm{~mol}^{-1}$, પાણીની ધનતા=1 $\mathrm{g} \mathrm{cm}^{-3}$
એસિટિક એસિડ $\mathrm{CH}_3 \mathrm{COOH} \rightleftharpoons \mathrm{CH}_3 \mathrm{COO}^{\ominus}+\mathrm{H}^{\oplus}$ તરીકે વિયોજિત થાય છે.
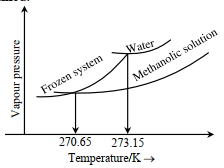
- 12જ્યારે'$x^{\prime} \times 10^{-2} \mathrm{~mL}$ મિથેનોલ (મોલર દળ=32 $\mathrm{g}$; ઘનતા $=0.792 \mathrm{~g} / \mathrm{cm}^3$ ) ને $100 \mathrm{~mL}$ પાણીમાં (ઘનતા $=1 \mathrm{~g} / \mathrm{cm}^3$ ), ઉમેરવામાં આવે છે ત્યારે નીચે મુજબ નો ડાયાગ્રામ પ્રાપ્ત થાય છે.View Solution
$(Image)$
$x=$.. . . . . .(નજીક નો પૂર્ણાક)
[આપેલ : $273.15 \mathrm{~K}$ પર પાણીનો મોલલ ઠારણ બિંદુ અવનયન અયળાંક $1.86 \mathrm{~K} \mathrm{~kg} \mathrm{~mol}^{-1}$ છે]
- 13નીચે આપેલ મુજબ નિર્બળ એસીડ $HX$ નું વિયોજન ધ્યાનમાં લો.View Solution
$\mathrm{HX}(\mathrm{aq}) \rightleftharpoons \mathrm{H}^{+}(\mathrm{aq})+\mathrm{X}(\mathrm{aq}), \mathrm{Ka}=1.2 \times 10^{-5}$
$\left[\mathrm{K}_{\mathrm{n}}:\right.$ વિયોજન અચળાંક]
$300 \mathrm{~K}$ પર $HX$ ના $0.03 \mathrm{M}$ જલીય દ્રાવણ નું અભિસરણ (પરાસરણ) દબાણ .......... $\times 10^{-2}$ bar છે.
$\left[\right.$ આપેલ : $\mathrm{R}=0.083 \mathrm{~L} \mathrm{bar} \mathrm{Mol}^{-1} \mathrm{~K}^{-1}$ ]
- 14પાણી અને અસિટીક એસિડ દરેક ના $2.7 kg$ ને મિશ્ર કરવામાં આવે છે. દ્રાવણ નું ઠાર બિંદુ - $x^{\circ} \mathrm{c}$ થશે. એવુ ધારી લો કે એસિટીક એસિડ પાણી માં ડાયમર બનાવતો નથી તેમજ પાણી માં વિયોજીત પણ થતો નથી. $x=$ ........... (નજીક પૂર્ણાક )View Solution
[ આપેલ: પાણી અને એસિટીક એસિડ નું મોલર દળ $18 \mathrm{~g} \mathrm{~mol}^{-1}$ અને $60 \mathrm{~g} \mathrm{~mol}^{-1}$ છે. પાણી નું ઠાર બિંદુ= $273 \mathrm{~K}$
એસિટીક એસિડ નું ઠાર બિંદુ = $290 \mathrm{~K}$
- 15$273$ $K$ પ૨ એક મંદ દ્રાવણનું અભિસરણ (પરાસરણ) દબાણ $7 \times 10^5 \mathrm{~Pa}$ છે. $283 \mathrm{~K}$ પર તે જ દ્રાવણનું અભિસરણ દબાણ________$\times 10^4 \mathrm{Nm}^{-2}$છે.View Solution
- 16આપણી પાસે ત્રણ $NaCl$ ના જલીય દ્રાવણો છે જેને $'A'$, $'B'$ અને $'C'$ તરીકે (દ્રારા) લેબલ કરેલ છે, જેની સાંદ્રતા અનુક્રમે (ક્રમશ:) $0.1 \mathrm{M}, 0.01 \mathrm{M}$ અને $0.001 \mathrm{M}$ છે. આ દ્રાવણો માટે વાન્ટ હોફ અવયવ ($1$) નું મૂલ્ય ક્રમમાં શું હશે?View Solution
- 17View Solutionજ્યારે થોડીક માત્રામાં નેપ્થોલિનને બેન્ઝિનમાં ઉમેરવામાં આવે છે ત્યારે બેન્ઝિનના ઠારબિંદુમાં શું થાય છે ?
- 18View Solutionનીચે આપેલા દ્રાવણોમાંથી ઠારબિંદુમાં સૌથી વધુ અવનયન.ન્યુનત્તમ (સૌથી ઓછું) ઠારબિંદુ શોધો.
- 19View Solutionનીચે પૈકી ક્યું મિશ્રણ રાઉલ્ટના નિયમથી ધન વિચલન દર્શાવે છે.
- 20પાણીનું ગલનબિંદુ $-24^{\circ} \mathrm{C}$ જેટલું જાળવી રાખવા માટે $18.6 \mathrm{~kg}$ પાણીમાં ઈથિલીન ગ્લાયકોલનું $kg$ દળ ઉમેરવામાં આવે છે. (ઈથિલીન ગ્લાયકોલનું મોલર દળ $62 \mathrm{~g} \mathrm{~mol}^{-1}$ છે. , પાણીનો $K_f=1.86 \mathrm{~K} \mathrm{~kg}$ $\left.\mathrm{mol}^{-1}\right) $View Solution
- 21View Solutionરાઉલ્ટના નિયમથી ઋણ વિચલન દર્શાવતા મિશ્ર થાય તેવા બે પ્રવાહીઓના એક દ્રાવણ નું___________.
- 22$0.004\,M\,K _2 SO _4$ નું દ્રાવણ એ $0.01\,M$ ગ્લુકોઝના દ્રાવણ સાથે સમદાબી છે. $K _2 SO _4$ નું ટકાવાર વિયોજન $...........$ છે. (નજીકનો પૂર્ણાક)View Solution
- 23$12\,g$ એક વિદ્યુત-અવિભાજ્ય $(A)$નું દ્રાવણ જ્યારે $1000\,mL$ પાણીમાં ઓગાળવામાં આવે છે ત્યારે લાગતું અભિસરણ દબાણ એ તે જ તાપમાન પર $0.05\,M$ ગ્લુકોઝ દ્રાવણ ના અભિસરણ દબાણ જેટલું જ છે.$A$ નું પ્રમાણ સૂચક સૂત્ર $CH _2 O$ છે.તો $A$નું આણ્વીય દળ $........\,g$ છે.(નજીકનો પૂર્ણાક)View Solution
- 24$20\%$ એસિટીક એસિડનું વિયોજન થાય છે કે જ્યારે તેના $5\,g$ ને $500\,mL$ પાણીમાં ઉમેરવામાં આવે છે. આવા પાણીનું ઠારબિંદુમાં અવનયન $.....\times 10^{–3}\;{ }^{\circ}C$ છે.(નજીકનાં પૂર્ણાંકમાં)View Solution
$C,H$ અને $O$ નું પરમાણ્યિ દળ અનુક્રમે $12,1$ અને $16\,a.m.u.$ છે.
[પાણીનો મોલલ અવનયન અચળાંક અને ઘનતા અનુક્રમે $1.86\,K\,kg\,mol^{-1}$ અને $1\,g\,cm$ છે.]
- 25$25^{\circ}\,C$ પર ગ્લુકોઝના $30\% (w/v)$ જલીય દ્વાવણ નું બાષ્પ દબાણ $.........\,mm\,Hg$ છે.(આપેલઃ ગ્લુકોઝના $30 \%$ (w/v) જલીય દ્વાવણની ધનતા $1.2\,g\,cm ^{-3}$ છે અને શુદ્ધ પાણીનું બાષ્પ દબાણ $24\,mm\,Hg$ છે) (ગ્લુકોઝનું મોલર દળ $180\,g\,mol ^{-1}$ છે.)View Solution
- 26$27^{\circ}\,C$ અને $1$ વાતા. દબાાણ પર, $SO _2( g )+\frac{1}{2} O _2( g )= SO _3( g )$ પ્રક્રિયા માટે,$K _{ p }=2 \times 10^{12} છ$. આ જ પ્રક્રિયા માટે $K _{ c }.......\times 10^{13}$ છે.View Solution
(આપેલ : $R =0.083\,L\,bar\,K ^{-1}\,mol ^{-1}$ )
- 27$2\,g$ "$X$" ને $1\,mole\,water$ માં ઉમેરીને એક દ્રાવણ તૈયાર કરવામાં આવ્યું દ્રાવણ મા "$X$" નું દળ ટકાવાર $...........\%$View Solution
- 28$2\,g$ અબાષ્પશીલ દ્રાવ્ય $(solute)$ ને $20\,g$ પાણીમાં ઓગાળીને બનાવેલું દ્રાવણ $373.52\,K$ પર ઉકળે છે.તો દ્રાવ્યનું આણ્વીય દળ. $........g\,mol^{-1}$ છે.(નજીકનો પૂર્ણાંક) પાણી $373\,K$ પર ઉકળે છે.(આપેલ છે પાણીનો $= 0.52\,K\,kg\,mol^{-1})$View Solution
- 29$300\,cm ^3$ કદનું એક જલીય દ્રાવણ એ $0.63\,g$ પ્રોટીન ધરાવે છે.$300\,K$ પર દ્રાવણનું અભિસરણ દબાણ $1.29\,mbar$ છે.પ્રોટીનનું મોલર દળ $.........\,g\,mol ^{-1}$ છે.આપેલ : $R =0.083\,L\,bar\,K ^{-1}\, mol ^{-1}$View Solution
- 30જલીય દ્રાવણમાં $MgCl _2$ ના $80\,mole$ ટકાવાર વિયોજીત થાય છે.$38^{\circ} C$ પર $MgCl _2$ ના $1.0\,molal$ જલીય દ્રાવણનું બાષ્પ દબાણ $.......\,mm\,Hg$ છે.(નજીકની પૂર્ણાક) આપેલ : $38^{\circ}\,C$ પર પાણીનું બાષ્પદબાણ $50\,mm\,Hg)$ છે.View Solution
- 31જો નિર્બળ મોનોબેઝિક એસિડના જલીય દ્રાવણનો વિયોજન અંશ $0.3$ શોધવામાં આવેલ હોય તો, પછી જોવા મળતું ઠારબિંદુ (મળી આવેલ ઠારબિંદુ) એ અપેક્ષિત / સૈધાંતિક ઠારબિંદુ કરતાં $........\%$ વધારે (ઊંયું) જોવા મળશે. (નજીકનો પૂર્ણાક)View Solution
- 32જો બે દ્રાવકો $X$ અને $Y$ (સમાન અણુભાર ધરાવતા હોય)ના ઉત્કલનબિંદુ $2:1$ ના ગુણોત્તરમાં હોય તો અને તેમની બાષ્પન એન્થાલ્પી $1:2$ ના ગુણોત્તર માં છે.$X$ નો ઉત્કલનબિંદુ ઉન્નયન અચળાંક એ $Y$ ના ઉત્કલનબિંદુુુ ઉન્નયન અચળાંક કરતા $m$ ગણો છે. તો $m$ નું મૂલ્ય $......$ છે.(નજીકનો પૂર્ણાક)View Solution
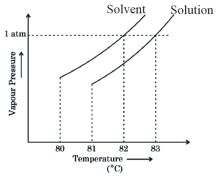
- 33દ્રાવણ દ્રાવક પ્રણાલી માટે બાષ્પ દબાણ વિરુદ્ધ તાપમાન નો વક્ર નીચે દર્શાવેલ છે.દ્રાવક નું ઉત્કલનબિંદુ $......$ ${ }^{\circ} C$ છે.View Solution
- 34નીચે બે વિધાનો આપેલા છે એક ને કથન $A$ વડે લેબલ કરેલ છે.અને બીજાને કારણ $R$ વડે લેબલ કરેલ છે.View Solution
કથન $A:$ $3.1500\,g$ જલયુક્ત ઓક્ઝેલિક એસિડ ને પાર્ટીમાં ઓગાળીને $2500\,m$ દ્વાવણ બનાવવામાં આવતા પરિણામે $0.1\,M$ ઓકઝેલિક એસિડ દ્વાવણ બનશે.
કારણ $R:$ યુક્ત ઓક્ઝેલિક એસિડ નું મોલર દળ $126\,g\,mol^{-1}$ છે.
ઉપરના વિધાનોના સંદર્ભમાં, નીચે આપેલા વિકલ્પો માંથી સાચો જવાબ પસંદ કરો.
- 35પાણીનું બાષ્પદબાણ $25 \%$ ધટાડવાના ક્રમમાં $1000\,g$ પાણીમા ઓગાળવા માટે જરૂરી યુરિયા $\left( NH _2 CONH _2\right)$ નું દળ $.........$ છે. (નજીક નો પૂર્ણાક) આપેલ :$N,C,O$ અને $H$ ના મોલર દળ અનુક્રમે $14,12,16$ અને $1\,g\,mol ^{-1}$ છે.View Solution
- 36બાષ્પ દબાણ $0.20\,mm\,Hg$ ઓછું કરવા માટે $100\,g$ પાણીમાં ગ્લુકોઝનું કેટલું વજન ઓગાળવું જોઈએ ?View Solution
(આપેલ :ઓરડાના તાપમાને શુદ્ધ પાણીનું બાષ્પ દબાણ $54.2\,mm\,Hg$ છે.ગ્લુકોઝ નું મોલર દળ $180\,g\,mol ^{-1}$ છે.)
- 37બે પ્રવાહી $A$ અને $B$ ને મિશ્ર કરવામાં આવે છે જ્યારે તેમના મોલ અંશ અનુક્રમે $0.7$ અને $0.3$ હોય ત્યારે કુલ દબાણ $350\,mm\,Hg$ જોવા મલ્યું જો મોલ અંશ માં ફેરફાર $0.2$ અને $0.8$ અનુક્રમે $A$ અને $B$ માટે કરવામાં આવે તો કુલ દબાણ $410\,mm\,Hg$ થાય છે. શુદ્ધ $A$ નું બાષ્પદબાણ $............mm Hg$. પ્રવાહીઓ અને દ્રાવણો ની આદર્શ વર્તણૂંક છે તે માની લો.View Solution
- 38સૂચી $-I$ ને સૂચી $- II$ સાથે જોડો.View Solution
સૂચી $-I$ સૂચી $- II$ $A$ વોન્ટ હોફ અવયવ, $i$ $I$ હિમાંક અચળાંક $B$ $k_f$ $II$ સમદાબી દ્રાવણો $C$ સમાન અભિસરણ દબાણ ધરાવતા દ્રાવણો $III$ સામાન્ય મોલર દળ/અસામાન્ય મોલર દળ $D$ એઝિયોટ્રોપ $IV$ તેની ઉપર બાષ્પના સમાન સંઘટન સાથેનું દ્રાવણ નીચે આપેલા વિકલ્પોમાંથી સાચો જવાબ પસંદ કરો.
- 39$CH_2Cl_2(DCM)$ નું $2.6 \times 10^{-3}$ દ્રાવણ બનાવવા માટે અમુક પ્રમાણમાં ડાયક્લોરોમિથેન $(CH_2Cl_2)$ $671.141\,mL$ ક્લોરોફોર્મ $(CHCl_3)$ માં ઉમેરવામાં આવે છે.તો $DCM$ ની સાંદ્રતા $.....\,ppm$ (દળ વડે) છે.(નજીકનો પૂર્ણાંક)View Solution
આપેલું છેઃ પરમાણુ દળ $:c =12$$H=1,$$CI= 35.5$,$CHCl_3$ની ઘનતા$= 1.49\,g\,cm^3$
- 40`દ્રાવણના દળ થી (વડે) સમુદ્રનું પાણી $29.25 \%\,NaCl$ અને $19\, \% \,MgCl _2$ ધરાવે છે.સમુદ્રના પાણી નું સામાન્ય ઉત્કલન બિંદુ $........^{\circ}C$(નજીકનો પૂર્ણાક)બંને $NaCl$ અને $MgCl _2$ નું $100\,\%$ આયનીકરણ ધારી લો. આપેલ : $K _{ b }\left( H _2 O \right)=0.52\,K\,kg\,mol ^{-1}$ $NaCl$ અને $MgCl _2$ નું મોલર દળ અનુક્રમે $58.5$ અને $95\,g\,mol ^{-1}$ છે.View Solution
- 41નીચે આપેલ વિધાનો માટે તેમની શુધ્ધતા મૂલ્યાંકન કરો.View Solution
$A.$ $0.1\,M\,NaCl$ અને $0.1\,M$ યુરિયા માટે પાણીના ઉત્કલનબિંદુતાપમાનમાં ઉન્નયન સમાન બની રહેશે.
$B.$ તેમના સંયોજન (સંરચના)માં ફેરફાર વગર એઝિયોયોટ્રોપિક મિશ્રણ ઉકળે છે.
$C.$ અભિચરણ હંમેશા અતિઅભિસારી થી અલ્પઅભિસારી માં થાય છે.
$D.$ $4.09\,M$ મોલારિટી ધરાવતા $32 \% H _2 SO _4$ દ્રાવણની ધનતા આશરે $1.26\,gmL ^{-1}$ છે.
$E.$ જ્યારે $KI$ દ્વાવણન સિલ્વર નાઈટ્રિટ દ્વાવણ માં ઉમેરતા ઋણભાર વાળા સોલ $(sol)$ પ્રાપ્ત થાય છે.
નીચે આપેલા વિકલ્પોમાંથી સાચો જવાબ પસંદ કરો.
- 42નીચે આપેલા માંથી દ્વાવણોના યુગ્મોની સંખ્યા કે જે અભિસરણ દબાણનું સમાન ધરાવે છે તે $.........$ $(100\%$ આયનીકરણ ધારી લો)View Solution
$A.$ $0.500\,M\,C _2 H _5 OH ( aq )$ અને $0.25\, M\, KBr ( aq )$
$B.$ $0.100\,M\,K _4\left[ Fe ( CN )_6\right]$ (aq) અને $0.100\, M$ $FeSO _4\left( NH _4\right)_2 SO _4$ (aq)
$C.$ $0.05 \,M\, K _4\left[ Fe ( CN )_6\right]( aq )$ અને $0.25\, M\, NaCl$ (aq)
$D.$ $0.15\, M\, NaCl ( aq )$ અને $0.1\, M BaCl _2$ (aq)
$E.$ $0.02\, M\, KCl\, MgCl _{2 .} 6 H _2 O ( aq )$ અને $0.05\, M$ $KCl ( aq )$
- 43પ્રક્રિયા ન કરતાં બે વાયુઓ $X$ અને $Y$ અનુક્રમે $20$ અને $45\,g\,mol ^{-1}$ અણુભાર ધરાવે છે. તેમના અનુક્રમે $0.6$ અને $0.45\,g$ ને એક પાત્રમાં ભેગા મૂકવામાં આવે છે. અને મિશ્રણનું કુલ દબાણ $740\,mm\,Hg$ છે.વાયુ $X$નું આંશિક દબાણ $............\,mm\,Hg$ છે.(નજીકનો પૂર્ણાંક)View Solution
- 44લેડ સંગ્રાહક બેટરી $H _2 SO _4$ નું દ્રાવણ વજન થી $38\%$ ધરાવે છે. આ સાંદ્રતા એ વાન્ટહોફ અવયવ $2.67$ છે. તો જે તાપમાને બેટરી માં રહેલ દ્રાવણ જામી જાય તે તાપમાન જણાવો $............$ છે. (નજીકનો પૂર્ણાંક) આપેલ : $K _f=1.8\,K\,kg\,mol ^{-1}$View Solution
- 45$0.5\, mL\, L ^{-1}$ સાંદ્રતા વાળા ફોર્મિક એસીડના દ્રાવણનું ઠાર બિંદુમાં અવનયન $0.0405^{\circ} C$ જોવા મળ્યું. ફોર્મિક એસિડની ઘનતા $1.05\, gm\, mL ^{-1}$ છે. તો ફોર્મિક એસિડના દ્રાવણનો વોન્ટ હોક્ર અવયવ $.....$ છે.View Solution
($k _{ f }=1.86\,K\,kg\,mol ^{-1}$ )
- 46$1.5$ મોલલ ગ્લુકોઝનું પાણીમાં દ્રાવણ માટે ઉત્કલન બિંદુનો ઉન્નયન $4\,K$ છે. $4.5$ મોલલ ગ્લુકોઝના પાણીમાંના દ્રાવણ માટે ઠારણ બિંદુમાં અવનયન $4\,K$ છે. તો મોલલ ઉન્નયન અચળાંક અને મોલલ અવનયન અચળાંકનો ગુણોત્તર $\left( K _{ b } / K _{f}\right)\dots\dots$ છે.View Solution
- 47$1.80 \,g$ દ્રાવ્ય $A$ને $62.5\,cm^3$ ઈથેનોલમાં આગાળવામાં આવે છે અને આ દ્રાવણનું ઠારણ બિંદુ $155.1 \,K$ માલુમ પડ્યું. તો દ્રાવ્ય $A$નું મોલર દળ $....\,g mol ^{-1}$માં શોધો.View Solution
(આપેલઃ ઈથેનોલનું ઠારણ બિંદુ $156.0\, K$, ઈથેનોલની ધનતા $0.80\, g\, cm ^{-3}$, ઈથેનોલનો ઠારબિંદુ અવનયન અચળાંક $2.00\, K\, kg \,mol ^{-1}$ )
- 48$1\, g$ અબ્પાષ્પશીલ દ્રાવ્યો $X$ અને $Y$ને $1\, kg$ પાણીમાં ઓગાળીને અનુક્રમે બે દ્રાવણો $A$ અને $B$ બનાવવામાં આવ્યા. $A$ અને $B$ માટે ઠારણ બિંદુઓમાં અવનયનનો ગુણોત્તર $1:4$ મળી આવેલ છે. $X$ અને $Y$ના મોલરદળનો ગુણોત્તર શોધો.View Solution
- 49$25^{\circ} C$ પર ધન $A$ ના નિશ્ચિત જથ્થા (માત્રા) ને $100\, g$ પાણીમાં ઓગાળીને મંદ દ્રાવણ બનાવવામાં આવે છે, દ્રાવણનું બાષ્પદબાણ એ શુદ્ધ પાણી કરતા અડધું (one-half) ધટે છે. શુદ્ધ પાણીનું બાષ્પદબાણ $23.76 \,mm\,Hg$ છે. તો ઉમેરેલા દ્રાવ્ય $A$ ના મોલની સંખ્યા $.....$ છે. ( નજીકનો પૂર્ણાંક )View Solution
- 50$2.5 \times 10^{-3} kg$ દ્રાવ્યને (solute) $75 \times 10^{-3} kg$ પાણીમાં ઓગાળીને કરીને બનાવેલું એક દ્રાવણ $373.535\, K$ ઉકળે છે. તો દ્રાવ્યનો મોલર દળ...........$g\, mol ^{-1}$ થશે. [નજીકના પૂર્ણાંક] (આપેલું છે $:\,K _{ b }\left( H _{2} O \right)=0.52\, K\, kg\, mol { }^{-1}$ અને પાણીનું ઉત્કલન બિંદુ = $373.15 \,K$ )View Solution
- 51$300\,K$ પર લોહીનું (રક્તનું) અભિસરણ દબાણ $7.47\,bar$ છે. એક દર્દીની નસમાં ગ્લુકોઝ નાખવા $(inject)$ માટે તે લોહી સાથે (રક્ત સાથે) સમદાબી હોવું જોઈએ ગ્લુકોઝ દ્રાવણની સાંદ્રતા $gL ^{-1}$ માં $\dots\dots\dots$ છે.View Solution
$(R =0.083\, L\, bar \,K ^{-1} \,mol ^{-1})$ (નજીકનો પૂર્ણાંક)
- 52અબાષ્પશીલ દ્રાવ્ય $A$ ના $2\%$ જલીય દ્રાવણનું ઉત્કલન બિંદુ બીજા એક અબાષ્પશીલ દ્રાવ્ય $B$ ના $8\%$ જલીય દ્રાવણ જેટલું છે, તો $A$ અને $B$ ના અણુભાર વચ્ચેનો સંબંધ શો છે ?View Solution
- 53એક વિદ્યુત અવિભાજ્ય દ્રાવ્ય $A$નું $1$ મોલલ દ્રાવણ માટે ઉત્કલનબિંદુમાં ઉન્નયન $3\, K$ છે. તે જ દ્રાવકમાં $A$ ના $2$ મોલલ દ્રાવણના ઠારણ બિંદુમાં અવનયન $6 \,K$ છે. $K _{ b }$ અન $K _{ f }$ નો ગુણોત્તર $K _{ B } / K _{ F } 1: X$ છે, તો $X$ નું મૂલ્ય $.......$View Solution
- 54જો $O _2$ વાયુને $303\, K$ પર પાણીમાંથી પસાર કરવામાં આવે, તો $1$ લિટર પાણીમાં ઓગળેલા $O _2$ વાયુના $milli\, moles$ ની સંખ્યા $.....$ છે. (નજીકનો પૂર્ણાંક )View Solution
(આપેલ છે : હેન્રીના નિયમનો અચળાંક $O _2$ વાયુ માટે $303\, K$ તાપમાને $46.82\, k\, bar$ અને $O _2$ નું આંશિક દબાણ $=0.920 \, bar )$
- 55પાણીમાં દ્રાવ્ય $A$ સુયોજિત થાય છે. જ્યારે $0.7\,g$ દ્રાવ્ય $A$ને $42.0\,g$ પાણીમાં ઓગાળવામાં આવે છે. ત્યારે $0.2{ }^{\circ}\,C$ વડે ઠારબિંદુમાં અવનયન થાય છે.તો પાણીમાં દ્રાવ્ય $A$ના સુયોજનની ટકાવારી $\dots\dots\dots$ $.....\,\%$ છે.View Solution
[આપેલ :દ્રાવ્ય $A$નું મોલર દળ $93\, g\, mol ^{-1}$. પાણીનો મોલલ અવનયન અચળાક $1.86\, K \,kg\, mol ^{-1}$ ]
- 56બાષ્પશીલ પ્રવાહી $A$ અને $B$ નું $25^{\circ}\,C$ પર બાષ્પદબાણ અનુક્રમે $50\,torr$ અને $100\,torr$ છે.જો પ્રવાહી મિશ્રણમાં $A$ ના $0.3$ મોલ અંશ ધરાવતું હોય તો, બાષ્પ અવસ્થામાં પ્રવાહી $B$ ના મોલ અંશ $\frac{x}{17}$ છે. તો $x$ નું $\dots\dots$ મૂલ્ચ છે.View Solution
- 57બે તત્વો $A$ અને $B , 0.15\, moles \,A _{2} B$ અને $AB _{3}$ પ્રકારના સંયોજનો બનાવે છે. જો $A _{2} B$ અને $AB _{3}$ બંને સમભારીય હોય, તો $B$ ના પરમાણ્વીય ભાર કરતા $A$ નો............ ગણો છે.View Solution
- 58બે પદાર્થો $A$ અને $B$ નું વાયુરૂપ મિશ્રણ, $0.8\,atm$ના કુલ દબાણે, આદર્શ પ્રવાહી દ્રાવણ સાથે સંતુલનમાં છે. પદાર્થ $A$ના બાષ્પઅવસ્થામાં મોલ અંશ (mole fraction) $0.5$ અને પ્રવાહી અવસ્થામાં $0.2$ છ. તો શુધ્ધ પ્રવાહી $A$ નું બાષ્પદબ્ધાણ $.....\,atm$ છે. (નજીકના પૂર્ણાંકમાં)View Solution
- 59$27^{\circ}\,C\,200\,mL$ પાણીમાં $2.0\,g$ પ્રોટીન જેનું મોલર દળ $60\,kg\,mol ^{-1}$ છે તે ઓગાળવામાં આવ્યું તો આ દ્રાવણ દ્વારા લાગતું અભિસરણ દબાણ $\dots\dots\dots$View Solution
(ઉપયોગ $R$ $=0.083\,L\,bar\,K ^{-1}\,mol ^{-1}$ )
- 60$1.2\,mL$ એસિટિકને પાણીમાં ઓગાળીને તેનું $2.0\,L$ દ્રાવણ બનાવ્યું. એસિડનાં સામર્થ્યમાં ઠારબિંદુ અવનયન $0.0198^{0}\,C$ જોવા મળ્યું.આ એસિડના વિયોજનની ટકાવારી $\dots\dots$છે. (નજીકનો પૂર્ણાંક)View Solution
[આપેલ : એસિટિક એસિડની ધનતા $1.02\,g\,mL ^{-1}$ છે.એસિટિક એસિડનું મોલર દળ $60\,g\,mol ^{-1}$ છે.$\left. K _{f}\left( H _{2} O \right)=1.85 K\,kg\,mol ^{-1}, K _{f}\left( H _{2} O \right)=1.85\,K\,kg\,mol ^{-1}\right]$
- 61ગ્લાયસિન $\left( C _{2} H _{5} NO _{2}\right)$ ઘરાવતા $2.5 \,g$ પ્રોર્ટીનને પાણીમાં ઓગાળીને તેનું $500 \,mL$ દ્રાવણ બનાવવામાં આવ્યું. $300\, K$ પર આ દ્રાવણનું અભિસરણ દબાણ $5.03 \times 10^{-3}$ $bar$ માલૂમ પડયું. પ્રોટીનમાં હાજર ગ્લાયસીન એકમોની કુલ સંખ્યા......... છે. $\left[ R =0.083 L\right.$ $bar$ $\left.K ^{-1} mol ^{-1}\right]$View Solution
- 62પોટેશિયમ ક્લોરાઈડનું $0.5$ ટકાવાર દ્રાવણ $-0.24^{\circ}\,C$ પર ઠરે છે તે માલૂમ પડેલ છે.પોટેશિયમ ક્લોરાઈડના વિયોજન ની ટકાવારી $\dots\dots$છે.View Solution
(પાણી માટે મોલલ અવનયન અચળાંક $1.80\,K\,kg\,mol ^{-1}$ અને $KCl$ નું મોલર દળ $74.6\,g\,mol ^{-1}$ છે.)
- 63$1\, {~kg}$ $0.75$ મોલલ સુક્રોઝના જલીય દ્રાવણને $-4^{\circ} {C}$ સુધી ઠંડું કરી શકાય છે. બરફનો જથ્થો $......$ ($g$ માં) જે અલગ કરવામાં આવશે. (નજીકના પૂર્ણાંકમાં)View Solution
$\left[\right.$ આપેલ છે $\left.: {K}_{{f}}\left({H}_{2} {O}\right)=1.86\, {~K}\, {~kg}\, {~mol}^{-1}\right]$
- 64$298\, K$ અને $1\, atm$ પર, $224\, mL\, SO _{2(g)}$ ને $100\, mL\, 0.1\, M\, NaOH$ નાં દ્રાવણમાંથી પસાર કરવામાં આવે છે. ઉત્પન્ન થતો અબાષ્પશીલ દ્રાવ્ય ને $36\, g$ પાણીમાં દ્રાવ્ય કરવામાં આવે છે. દ્રાવણનાં બાષ્પદબાણમાં થતો ઘટાડો (lowering),(ધારી લો કે દ્રાવણ મંદ છે.) $\left( P _{\left( H _{2} O \right)}^{\circ}=24\, mm \right.$ of $\left. Hg \right) x \times 10^{-2} \,mm$ of $Hg$ છે. તો $x$ નું મૂલ્ય ........... છે. (પૂર્ણાક જવાબ)View Solution
- 65$298\, {~K}$ પર સોફ્ટ ડ્રિંકના ઉત્પાદનમાં પ્રક્રિયા દરમિયાન ${CO}_{2}$ વાયુ પાણી દ્વારા પરપોટામાં આવે છે. જો ${CO}_{2}$ $0.835$ બારનું આંશિક દબાણ લાવે તો ${CO}_{2}$ના $x \,{~m} \,{~mol}$ $0.9\,{~L}$ પાણીમાં ઓગળી જશે. $x$નું મૂલ્ય $.....$ (નજીકના પૂર્ણાંકમાં) છે.View Solution
($298\, {~K}$ એ હેન્રીના નિયમનો અચળાંક ${CO}_{2}$ માટે $1.67 \times 10^{3}$ બાર છે.)
- 66$363\, K$ પર,$A$ નું બાષ્પ દબાણ $21 \,kPa$ અને $B$ નું $18 \,kPa$ છે. $A$ નાં એક મોલ અને $B$ નાં $2$ મોલ્સ (moles) ને મિશ્ર કરવામાં આવે છે. ધારી લો કે આ દ્રાવણ આદર્શ છે. મિશ્રણનું બાષ્પદબાણ $...... \,kPa$ છે. (નજીકનાં પૂર્ણાંકમાં રાઉન્ડ ઓફ કરો)View Solution
- 67$40\, {~g}$ ગ્લુકોઝ (મોલર દળ $=180$ ) $200\, {~mL}$ પાણી સાથે મિશ્રિત થાય છે. દ્રાવણનું ઠારબિંદુ $.....\,{K}$. (નજીકના પૂર્ણાંકમાં)View Solution
[આપેલ છે: ${K}_{{f}}=1.86 \,{~K} \,{~kg} \,{~mol}^{-1} ;$ પાણીની ઘનતા $=$ $1.00 \,{~g}\, {~cm}^{-3} ;$ પાણીનું ઠારબિંદુ $\left.=273.15\, {~K}\right]$
- 68$5.5^{\circ} C$ પર $C _{6} H _{6}$ ઠારણ પામે છે. તો $C _{4} H _{10}$ ના $10\, g$ નું $200\, g$ $C _{6} H _{6}$ માં બનાવેલું દ્રાવણ ..... ${ }^{\circ} C$ તાપમાન પર ઠરશે. (બેન્ઝીનનો મોલલ ઠારબિંદુ અવનયન અચળાંક $5.12\,{ }^{\circ} C / m$ છે)View Solution
- 69$83\, {~g}$ ઇથિલિન ગ્લાયકોલ $625\, {~g}$ પાણીમાં ઓગળેલ છે. દ્રાવણનું ઠાર બિંદુ $......\, {K}$ છે. (નજીકના પૂર્ણાંકમાં)View Solution
[ઉપયોગ કરો: પાણીનો મોલલ અવનયન મંદન અચળાંક $\left.=1.86 \,{~K} \,{~kg} \,{~mol}^{-1}\right]$
પાણીનું ઠારબિંદુ $=273\, {~K}$
આણ્વિય દળ : ${C}: 12.0\, {u}, {O}: 16.0\, {u}, {H}: 1.0\, {u}]$
- 70$AB _{2}$ એ પાણીમાં $A ^{2+}$ અને $B ^{-}$ સ્વરૂપે વિયોજન થયેલ છે. $AB _{2}$ના $10.0$ મોલલ જલીય દ્રાવણનો ઉત્કલન બિંદુ એ ............ ${ }^{\circ} C$ છે.View Solution
[આપેલ છે: પાણીનો મોલલ ઉન્નયન અચળાંક $K _{ b }=0.5\, \,K\, kg\, mol ^{-1}$ શુદ્ધ પાણીનું ઉત્કલન બિંદુ $\left.=100^{\circ} C \right]$
- 71$1$ મોલલ $K _{4} Fe ( CN )_{6} $ દ્રાવણમાં $0.4 .$ નું વિયોજન થાય છે. તેનું ઉત્કલન બિંદુ અન્ય દ્રાવણ ની સમાન હોય છે જેમાં $18.1$ વિદ્યુતઅવિભાજ્ય્ય દ્રાવકના ટકાની ટકાવારી હોય છે.$A$ નું મોલર દળ $.......\, u$. છેView Solution
- 72એક સંયોજન $AB$ જલીય દ્રાવણમાં $75 \,\%$ સુધી વિયોજન પામે છે. દ્રાવણની મોલાલિટી કે જે દ્રાવણનું ઉત્કલન બિંદુમાં $2.5\, K$ નો વધારો દર્શાવે છે તો તે ..... મોલલ છે.View Solution
(નજીકનાં પૂર્ણાંકમાં રાઉન્ડ ઑફ) $\left[ K _{ b }=0.52 \,K \,kg \,mol ^{-1}\right]$
- 73જો $5 \,{~L}$ દ્રાવણ બનાવવા માટે $80\, {~g}$ કોપર સલ્ફેટ ${CuSO}_{4} \cdot{ } {5 {H}_{2} {O}}$ આયનીકૃત પાણીમાં ઓગળે છે. કોપર સલ્ફેટ દ્રાવણની સાંદ્રતા ${x} \times 10^{-3}\, {~mol}\, {~L}^{-1}$ છે.${x}$નું મૂલ્ય $......$ છે.View Solution
[આણ્વીય દળ ${Cu}: 63.54\, {u}, {S}: 32\, {u}, {O}: 16 \,{u}, {H}: 1\, {u}]$
- 74જ્યારે $10\, {~mL}$ ${KMnO}_{4}$ના જલીય દ્રાવણના એસિડિક માધ્યમમાં ટાઇટ્રેટેડ હતા, ત્યારે ફેરસ સલ્ફેટના જલીય દ્રાવણના $0.1$ ${M}$નું સમાન કદ પૂર્ણ કરવા માટે રંગનું મુક્ત થવું જરૂરી હતું. ${KMnO}_{4}$ની સાંદ્રતા ગ્રામ પ્રતિ લિટરમાં $......\,\times 10^{-2}$ છે. (નજીકના પૂર્ણાંકમાં)View Solution
આણ્વિય દળ ${K}=39, {Mn}=55, {O}=16]$
- 75જ્યારે $9.45\,g$ $ClCH _{2} COOH$ ને $500\, mL$ પાણીમાં ઉમેરવામાં આવે છે ત્યારે તેનું ઠારણ બિંદુ $0.5°C$ નીચું જાય છે. તો $ClCH _{2} COOH$ નો વિયોજન અચળાંક $x \times 10^{-3}$ છે. તો $x$ નું મૂલ્ય ....... છે. $\left[ K _{f\left( H _{2} O \right)}=1.86\, K\, kg \,mol ^{-1}\right]$ (નજીકના પૂણાંકમાં રાઉન્ડ ઑફ)View Solution
- 76નિર્બળ એસિડનું $2$ દ્રાવણ $HA$ માં $3.885^{\circ} C$ નો ઠંડક છે.. આ એસિડનો વિયોજન અંશ ...... $\times 10^{-3} .$ છેView Solution
[અહી આપેલ : પાણીનો મોલલ અચળાંક= $1.85 \,K \,kg \,mol ^{-1}$ શુદ્ધ પાણીનો ઠંડક $\left.=0^{\circ} C \right]$
- 77નીચેના ચાર જલીય દ્રાવણોમાંથી, તે દ્રાવણની કુલ સંખ્યા જેમનું ઠારબિંદુ $0.10\, {M} {C}_{2} {H}_{5} {OH}$ કરતા ઓછું છે. (પૂર્ણાંક જવાબ)View Solution
$(i)$ $0.10\, {M} \,{Ba}_{3}\left({PO}_{4}\right)_{2}$
$(ii)$ $0.10\, {M}\, {Na}_{2} {SO}_{4}$
$(iii)$ $0.10\, {M}\, {KCl}$
$(iv)$ $0.10 \,{M} \,{Li}_{3} {PO}_{4}$
- 78નીચેનામાંથી કયુ $0.06 \, {M}$ જલીય દ્રાવણમાં સૌથી નીચુ ઠારબિંદુ ધરાવે છે?View Solution
- 79નીચેનામાંથી કયું $0.10\, {M}$ જલીય દ્રાવણ સૌથી મોટા ફ્રીઝિંગ પોઇન્ટ ડિપ્રેશનનું પ્રદર્શન કરશે?View Solution
- 80પાણી ઉપરની વરાળમાં પાણીમાં ઓગળેલ ઓક્સિજનનું આંશિક દબાણ $20\, kPa$ હોય છે . પાણીમાં ઓક્સિજનની મોલર દ્રાવ્યતા ............ $-\times 10^{-5}\, mol\, dm ^{-3}$View Solution
[આપેલ છે: $O _{2}$ માટે હેન્રી અચળાંકનો નિયમ $= K _{ H }=8.0 \times 10^{4} kPa$ , ઓગળેલા ઓક્સિજન સાથે પાણીની ઘનતા $=1.0\, kg\, dm ^{-3}$ ]
- 81એક મોલલ વિદ્યુત વિભાજ્ય $A _{2} B _{3}$ નું જલીય દ્રાવણ $60\%$ આયનીકરણ પામેલ છે. તો $1\,atm$ પર, આ દ્રાવણનું ઉત્કલન બિંદુ .......... $K$ છે. (નજીકના પૂર્ણાકમાં રાઉન્ડ ઑફ)View Solution
[આપેલ $K_b (H_2O) = 0.52\, K\, kg\, mol^{-1}]$
- 82$1.22\, {~g}$ એક કાર્બનિક એસિડ $100 \,{~g}$ બેન્ઝીન $\left({K}_{{b}}=2.6\, {~K}\, {~kg} \,{~mol}^{-1}\right)$ અને $100\, {~g}$ એસિટોન $ 100 \, {~ g} $ $\left({K}_{b}=1.7\, {~K} \,{~kg} \,{~mol}^{-1}\right) .$ માં જુદા-જુદા ઓગળેલ છે.એસિડ બેન્ઝીનમાં ડાઇમરાઇઝ કરવા માટે જાણીતું છે પરંતુ એસિટોનમાં મોનોમર તરીકે રહે છે.એસિટોનમાં દ્રાવણનું ઉત્કલનબિંદુ $0.17^{\circ} {C}$ જેટલું વધે છે.View Solution
બેન્ઝીનના દ્રાવણમાં ઉત્કલન બિંદુમાં વધારો ${ }^{\circ} {C}$માં ${x} \times 10^{-2}$ છે.${x}$નું મૂલ્ય $.....$ છે.(નજીકના પૂર્ણાંકમાં)
$[$ આણ્વિય દળ : ${C}=12.0, {H}=1.0, {O}=16.0]$
- 83$1.46 \,{~g}$ જૈવપોલિમર $100\, {~mL}$ પાણીમાં ઓગળેલ છે; $300\, {~K}$ એ $2.42 \times 10^{-3}$ બારનું અભિસરણ દબાણ લગાવ્યું. જૈવપોલિમરનો મોલર દળ $.....\,\times 10^{4} \,{~g}\,{~mol}^{-1}$ છે.View Solution
[ઉપયોગ : ${R}=0.083\, {~L}\, bar \,{mol}^{-1} \,{~K}^{-1}$ ]
- 84$20^{\circ} {C}$ પર બેન્ઝીનનું બાષ્પદબાણ $70$ ટોર અને મિથાઈલ બેન્ઝીનનું $20$ ટોર છે. $20^{\circ} {C}$ પર બાષ્પના તબક્કામાં બેન્ઝીનનો મોલઅંશ બેન્ઝીન અને મિથાઈલ બેન્ઝિનના સમકક્ષ મિશ્રણ ઉપર $.....\,\times 10^{-2}$ (નજીકના પૂર્ણાંકમાં)View Solution
- 85$25^{\circ} {C}$ પર $A$ અને $B$ નું બાષ્પદબાણ $90\, {~mm}\, {Hg}$ અને $15\, {~mm} \,{Hg}$ અનુક્રમે છે.જો ${A}$ અને ${B}$ મિશ્રિત હોય કે મિશ્રણમાં $A$ નો મોલ-અંશ $0.6$ હોય, તો બાષ્પના તબક્કામાં $B$ નો મોલ-અંશ $x \times 10^{-1}.$ $x$નું મૂલ્ય $.....$ (નજીકના પૂર્ણાંકમાં)View Solution
- 86$4 {~g}$ ${NaOH}$ અને ${Na}_{2} {CO}_{3}$નું ${x}\, {g}$ ${NaOH}$ અને ${y}\, {g}$ ${Na}_{2} {CO}_{3}$નું સમમોલર મિશ્રણ છે.$x$નું મૂલ્ય $.....\,g.$ (નજીકના પૂર્ણાંકમાં)View Solution
- 87દ્રાવકમાં $50\, \%$ એસિડ $HA$ ડાઇમેરાઇઝ થાય છે અને બાકીનું વિઘટન થાય છે. એસિડનું વોન્ટ હોફ અવયવ $.....\,\times 10^{-2}$ છે.View Solution
- 88$0.10\, m$ જલીય $CrCl _{3}, xNH _{3}$નું ઉન્નયન ઉત્કલન બિંદુ એ $0.05\, m$ જલીય $CaCl _{2}$ દ્રાવણ કરતાં બે ગણું છે. $x$નું મૂલ્ય ......... છે.View Solution
$[$ધારો કે સંકીર્ણનું $100 \%$ આયાનીકરણ થાય છે અને $CaCl _{2}$માં $Cr$નો સવાર્ગંક $6$ છે અને બધા $NH _{3}$ પરમાણુ સવર્ગ ક્ષેત્રમાં અંદર હાજર છે. $]$
- 89$1.03\; \mathrm{g} / \mathrm{mL}$ ઘનતાના રામુદ્રના પાણીના એક લિટરમાં $10.30\; \mathrm{mg}\,\,\mathrm{O}_{2}$ દ્રાવ્ય થાય છે. તો $ppm$ માં $\mathrm{O}_{2}$ ની સાંદ્રતા. . . ..View Solution
- 90$298\, K$ પર જો $250\, cm ^{3}$ ધરાવતા જલીય દ્રાવણનો, સમઅભિસારી હોય તો તે અન્ય જલીય દ્રાવણના એક લિટર સાથે $1.65\, g$ પ્રોટીન $B ,$ પર હોય છે.$A$ અને $B$ના આણ્વિય દળનો ગુણોતર ..........$\times 10^{-2}$ (નજીકના અંક સુધી)View Solution
- 91$300\ K$ પર, $n-$ હેક્ઝેનના $1$ મોલ અને $n-$ હેપ્ટેનના $3$ મોલ્સ ધરાવતા દ્રાવણનું બાષ્પ દબાણ $Hg$ના $550\, mm$ છે.એ જ તાપમાને, જો આ દ્રાવણમાં $n-$હેપ્ટેનનો વધુ એક મોલ ઉમેરવામાં આવે છે, તો દ્રાવણનું બાષ્પ દબાણ $Hg$ના $10\, mm$ દ્વારા વધે છે.શુદ્ધ અવસ્થામાં $n-$ હેપ્ટેનના $mm Hg$ માં બાષ્પ દબાણ ..........$?$View Solution
- 92$H _{2}, He$ અને $O _{2}$ દરેકના એક મોલનું મિશ્રણ તાપમાન $T$ પરકદ $V$ ના સિલિન્ડરમાં બંધ છે.$H _{2}$ નું આંશિક દબાણ $2$ atm છે સિલિન્ડરમાં વાયુઓનો કુલ દબાણ $.......atm$View Solution
- 93$NaCl$ દ્રાવણનું અભિસરણ દબાણ $0.10$ $atm$ છે અને ગ્લુકોઝ દ્રાવણનું અભિસરણ દબાણ $0.20$ $atm.$ છે. $1\, L$ ગ્લુકોઝ દ્રાવણ અને $2\, L$ સોડિયમ ક્લોરાઇડ દ્રાવણ સાથે મિશ્ર કરતા બનતા દ્રાવણનું અભિસરણ દબાણ $x \times 10^{-3}$ atm છે.$x$ .......... છે.(નજીકના અંક)View Solution
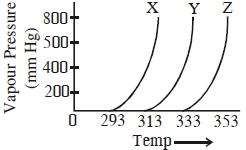
- 94ત્રણ જુદા જુદા પ્રવાહીઓ $X, Y$ અને $Z$ માટે બાષ્પદબાણ અને તાપમાનનો આલેખ નીચે દર્શાવ્યો છે. નીચેના તારણો કરવામાં આવ્યા.View Solution
(A)$Y$ ની સરખામણીમાં $\mathrm{X}$ માં આંતરઆણ્વિય આંતરક્રિયા વધુ છે
(B)$Y$ ની સરખામણીમાં $\mathrm{X}$ માં આંતરઆણ્વિય આંતરક્રિયા ઓછી છે
(C)$Y$ ની સરખામણીમાં $\mathrm{Z}$ માં આંતરઆણ્વિય આંતરક્રિયા ઓછી છે
સાચું તારણ(ણો) જણાવો.
- 95દ્રાવણનો સેટ $180$ $g$ પાણી દ્રાવક તરીકે અને $10$ $g$ $A, B$ અને $C$ જુદા-જુદા અબાષ્પશીલ દ્રાવ્યોનો ઉપયોગ કરીને તૈયાર કરવામાં આવે છે.આ દ્રાવ્યોની હાજરીમાં સંબંધિત બાષ્પદબાણનું પ્રમાણ ઘટવું તેનો ક્રમ કયો છેView Solution
[$A =100 \,g\, mol ^{-1} ; B =200 \,g\, mol ^{-1}$$ C =10,000 \,g\, mol ^{-1}$ના મોલર દળ આપેલ છે ]
- 96પાણીનું ઠારબિંદુ ઘટાડીને $-0.2^{\circ} \mathrm{C} $ કરવા $600\; \mathrm{g}$ પાણી $(\rho=1.00\; \mathrm{g} / \mathrm{mL})$ માં $\mathrm{NaCl}$ નો કેટલો જથ્થો ઉમેરવો જોઇએ ? (પાણી માટે ઠારબિંદુ અવનયન અચળાંક $=2\; \mathrm{K}\; \mathrm{kg} \;\mathrm{mol}^{-1}$)View Solution
- 97હળવું પીણું ને ઓરડાના તાપમાને પ્રવાહી પર $3$ બારના આંશિક દબાણ $CO _{2}$ સાથે બોટલ્ડ કરવામાં આવી હતી. દ્રાવણ માં $CO _{2}$ નો આંશિક દબાણ $30$બારના મૂલ્ય સુધી પહોંચે છે જ્યારે $44$ ગ્રામ $CO _{2}$ ના $1$ તાપમાને, $1$ કિલોગ્રામ પાણીમાં ભળી જાય છે. હળવું પીણુંનું આશરે $ pH $ .......$\times 10^{-1}$ છે.View Solution
($H _{2} CO _{3}$ નો પ્રથમ વિયોજન અચળાંક =$4.0 \times 10^{-7}$$\log 2=0.3 ;$ હળવા પીણાં ની ઘનતા $=1\, g\, mL ^{-1})$
- 98$100\, mL$ દ્રાવણ $1.43\, g$ of $Na _{2} CO _{3} \cdot xH _{2} O $ ઉમેરીને બનાવવામાં આવ્યું હતું. દ્રાવણની નોર્માલિટી $0.1$ $N.$ છે. $x$નું મૂલ્ય......... ($Na$નું પરમાણ્વીય દળ $23\, g / mol$ છે ) :View Solution
- 99આર્સેનિક સલ્ફાઇડ માટે $\mathrm{HCl}$ નું ઉર્ણન મૂલ્ય $30\; \mathrm{m}\; mole \;\mathrm{L}^{-1} .$ છે. જો આર્સેનીક સલ્ફાઇડના સ્કંદન માટે $\mathrm{H}_{2} \mathrm{SO}_{4}$ નો ઉપયોગ કરવામાં આવે તો ઉપરોક્ત હેતુ માટે $250\; \mathrm{ml}$ માં જરૂરી $\mathrm{H}_{2} \mathrm{SO}_{4}$ સો ગ્રામમાં જથ્થો ...View Solution
(આણ્વિય દળ $\left.\mathrm{H}_{2} \mathrm{SO}_{4}=98 \;\mathrm{g} / \mathrm{mol}\right)$
- 100ચોક્કસ જથ્થાના વિધુત વડે $AgNO_3 (aq)$ ના દ્રાવણમાંથી $108\; \mathrm{g}$ સિલ્વર (મોલર દળ $=108\; \mathrm{g}\; \mathrm{mol}^{-1}$) કેથોડ પર જમા થાય છે, તો આટલા વિધુત જથ્થા વડે $273 \;\mathrm{K}$ અને $1$ બાર પર પાણીમાંથી ઉત્પન્ન થતા ઓક્સિજનનું કદ ............. $\mathrm{litre}$ જણાવો.View Solution