$1$ વાતાવરણ દબાણે પાણીનાં બાષ્પીભવન માટે $\Delta H$ અને $\Delta S$ ની કિંમત અનુક્રમે $40.63\,KJ/mol$ અને $108.8\,J/K.mol$ છે, તો .......$K$ તાપમાને તેની ગીબ્સ ઊર્જામાં થતો ફેરફાર ($\Delta G$) શૂન્ય થશે ?
Medium
Download our app for free and get started
c
$\Delta G$ = $\Delta H$ - $T\Delta S$ $\Delta G$ $= 0$ , $\Delta H$ = $T\Delta S$
$\Delta G$ = $\Delta H$ - $T\Delta S$ $\Delta G$ $= 0$ , $\Delta H$ = $T\Delta S$
$T\,\, = \frac{{40.63 \times {{10}^3}}}{{108.8}}\,\,\, = \,\,\,{\text{373}}{\text{.4 K}}$
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$1\,$ મોલ પાણીનું $5\,^oC$ થી $-5\,^oC$ તાપમાને ઠારણ કરવાનો એન્થાલ્પી ફેરફાર.......$kJ\, mol^{-1}$View Solution
(Given ${\Delta _{fus}}H = 6\, kJ\, mol^{-1}$ at $0\,^oC$,
$C_p(H_2O, l) =75.3\, J\, mol^{-1} \, K^{-1}$ ,
$C_p(H_2O, s) = 36.8\, J\, mol^{-1} \, K^{ -1}$ )
- 2બોમ્બ કેલેરીમીટરમાં એક મોલ ઝીંક રજ સાથે એક મોલ સલ્ફયુરીક એસિડની ઉષ્માક્ષેપક પ્રક્રિયા માટે $\Delta U$ અને $w$ નો સંબંધ .....View Solution
- 3પ્રક્રિયા $A \to B$ માટે $\Delta H = 4\,kcal\,mo{l^{ - 1}}$ અને $\Delta S = 10\,cal\,{K^{ - 1}}\,mo{l^{ - 1}}$ હોય, તો પ્રક્યિા .......$K$ તાપમાને સ્વયંભૂ હોઇ શકે ?View Solution
- 4જો $XY$, $X_2$ અને $Y_2$ ની બંધ તોડવા માટેની ઊર્જાનો ગુણોત્તર $1 : 1 : 0.5 $ અને $xy$ ની સર્જન ઉષ્મા $\Delta$$fH$ $+0.5a KJ/mol$ હોય તો $X_2$ ની બંધ તોડવા માટેની ઊર્જા .....$kJ\, mol^{-1}$ હશે.View Solution
- 5$2{H_2}{O_2}(\ell )\,\, \to \,\,2{H_2}O(\ell )\,\, + \,\,{O_2}_{(g)}$ પ્રક્રિયા માટે એન્થાલ્પીનો ફેરફાર કેટલો થશે ? જો ${H_2}{O_2}(\ell )$ અને ${H_2}{O}(\ell )$ ના નિર્માણની ઉષ્મા અનુક્રમે $-188$ અને $-286 \,KJ/$ મોલ છે.......$KJ/$મોલView Solution
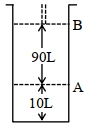
- 6આપેલ આક્રૂતિને ધ્યાનમાં લો.View Solution
$18^{\circ} \mathrm{C}$ પર, સ્થાન $A$ પર, પિસ્ટન સાથે જોડેલા (fitted) સિલિન્ડર માં આદર્શ વાયુનો $1$ $\mathrm{mol}$ રાખેલ છે. જો તાપમાન માં કોઈપણ જાતનો ફેરફાર ન કરીએ તો પિસ્ટન એ સ્થાન $B$ તરફ ખસે છે ત્યારે આ પ્રતિવર્તી પ્રક્રમ માં થયેલ કાર્ય $'x' L atm$ છે. $x=-$ ........... $L.atm$ (નજીક નો પૂર્ણાક)
[આપેલ : નિરપેક્ષ તાપમાન $={ }^{\circ} \mathrm{C}+273.15, \mathrm{R}=0.08206 \mathrm{~L} \mathrm{~atm} \mathrm{~mol}^{-1} \mathrm{~K}^{-1}$ ]
- 7આપેલ $CH_4, C_2H_4 $અને $ C_3H_8 $ની પ્રમાણિત નિર્માણ ઉષ્મા અનુક્રમે $-17.9, 12.5, -24.8 $ કિ કેલરી/મોલ છે. તો $CH_4 + C_2H_4 \rightarrow C_3H_8$ પ્રક્રિયા માટે $O H$......$Kcal$ થશે.View Solution
- 8નીચેની પ્રક્રિયા માટે આપેલ માહિતી નીચે મુજબ છે:View Solution
${FeO}_{(0)}+{C}_{\text {(gaplike) }} \longrightarrow {Fe}_{(0)}+{CO}_{({g})}$
પદાર્થ $\Delta {H}^{\circ}$
$\left({kJ} {mol}^{-1}\right)$
$\Delta {S}^{\circ}$
$\left({J} {mol}^{-1} {~K}^{-1}\right)$
${FeO}_{(s)}$ $-266.3$ $57.49$ ${C}_{\text {(graphite) }}$ $0$ $5.74$ ${Fe}_{(s)}$ $0$ $27.28$ ${CO}_{({g})}$ $-110.5$ $197.6$ ${K}$માં લઘુત્તમ તાપમાન કે જેના પર પ્રક્રિયા સ્વયંભૂ બને છે તે $.......$ છે.(પૂર્ણાંકમાં જવાબ)
- 9નીચે આપેલ પરિબળો દ્વારા જલીય દ્રાવણમાં ક્લોરીનની ઓક્સિડાઈઝ ક્ષમતા માપી શકાય છે. તો $1/2 Cl_2$$_{(g)}$ થી $Cl^{-}$ $_{(aq)}$માં રૂપાંતરણ થવા કેટલા .....$kJ\, mol^{-1}$ ઉર્જા ભાગ લેશે ?View Solution
$\frac{1}{2}C{l_2}_{(g)}\,\xrightarrow{{\frac{1}{2}{\Delta _{diss}}{H^\Theta }}}\,Cl_{(g)}\,\,\xrightarrow{{{\Delta _{eg}}{H^\Theta }}}\,\,C{l^ - }_{(g)}\,\xrightarrow{{{\Delta _{hyd}}{H^\Theta }}}\,C{l^ - }_{(aq)}$
$({\mkern 1mu} {\Delta _{diss}}{\mkern 1mu} H_{C{l_2}}^\Theta {\mkern 1mu} = {\mkern 1mu} {\mkern 1mu} 240{\mkern 1mu} {\mkern 1mu} kJ{\mkern 1mu} {\mkern 1mu} mo{l^{ - 1}},{\mkern 1mu} {\mkern 1mu} {\Delta _{eg}}{\mkern 1mu} H_{Cl}^\Theta {\mkern 1mu} = {\mkern 1mu} {\mkern 1mu} - 349{\mkern 1mu} {\mkern 1mu} kJ{\mkern 1mu} {\mkern 1mu} mo{l^{ - 1}},{\mkern 1mu} {\mkern 1mu} $
${\Delta _{hyd}}H_{C{l^ - }}^\Theta {\mkern 1mu} = {\mkern 1mu} {\mkern 1mu} - {\mkern 1mu} 381{\mkern 1mu} kJ{\mkern 1mu} {\mkern 1mu} mo{l^{ - 1}})$
- 10$4NH_3$$_{(g)}$ + $3O_2$$_{(g)}$ $\rightarrow$ $2N_2$$_{(g)}$ + $6H_2O_{(l)}$ પ્રક્રિયામાં ઉષ્મા પરિવર્તનની ગણતરી .....$KJ$ થશે.View Solution
$298 \,K \,NH_3$$_{(g)}$ અને $H_2O_{(l)}$ ની નિર્માણ ઉષ્મા અનુક્રમે $-46.0$ અને $-286.0\, kJ \,mol^{-}$ છે.