(Given ${\Delta _{fus}}H = 6\, kJ\, mol^{-1}$ at $0\,^oC$,
$C_p(H_2O, l) =75.3\, J\, mol^{-1} \, K^{-1}$ ,
$C_p(H_2O, s) = 36.8\, J\, mol^{-1} \, K^{ -1}$ )
In order to calculate the enthalpy change for $H_2O$ at $5\,^oC$ to ice at $-\,5\,^oC$ , we need to calculated the enthalpy change of all the transformation involved in the process.
$(a)$ Energy change of $1\,mol$, $H_2O\,(l)$, at $5\,^oC$
$\to \,1\,mol$, $H_2O\,(l)$ , $0\,^oC$
$(b)$ Energy change of $1\,mol$, $H_2O\,(l)$, at $0\,^oC$
$\to \,1\,mol$, $H_2O\,(s)$ (ice) , $0\,^oC$
$(c)$ Energy change of $1\,mol$, Ice $(s)$, at $0\,^oC$
$\to \,1\,mol$, Ice $(s)$ , $-5\,^oC$
Total $\Delta H$
$ = \,{C_P}\,[{H_2}O\,(l)]\,\,\Delta T\,\, + \,\Delta H$ freezing $ + \,\,{C_P}\,[{H_2}O\,(s)]\,\,\Delta T$
$ = \,(75.3\,\,J\,\,mo{l^{ - 1}}\,{K^{ - 1}})\,( - 5)\,K\, + ( - \,6\, \times \,{10^3}\,\,J\,mo{l^{ - 1}}\,{K^{ - 1}})$ $+ \,(36.8\,\,J\,mo{l^{ - 1}}\,{K^{ - 1}})\,( - 5)\,K$
$\Delta H\,\, = \,\, - \,6.56\,\,kJ\,mo{l^{ - 1}}$ (exothermic process)
So, $\Delta H\,\, = \,\,6.56\,\,kJ\,mo{l^{ - 1}}$
Download our appand get started for free
Similar Questions
- 1જ્યારે $5$ લિટર મિથેન અને પ્રોપેનનું વાયુ મિશ્રણ $0\,^oC$ અને $1$ વાતાવરણ એ સંપૂર્ણ રીતે ગોઠવાયેલ છે, ઓક્સિજનનું સમાન તાપમાન અને દબાણ પર $16$ લિટરનો વપરાશ થાય છે.આ દહનથી મુક્ત થતી ગરમીનું પ્રમાણ $kJ$માં $(\Delta H_{comb.} \, (CH_4) = 890\, kJ\, mol^{-1},$ $\Delta H_{comb.} (C_3H_8) = kJ \,mol^{-1})$ શું હશે?View Solution
- 2View Solutionપ્રક્રિયાનો સ્યંભૂ ગુણધર્મ અશક્ય છે. જો ........
- 3$N_2O_4$ ના વિઘટનની પ્રક્રિયા માટે $\Delta H = 58.04$ કિલોજૂલ અને $\Delta S = 176.7$ જૂલ/કેલ્વિન છે, તો $\Delta G = .......$ કિલોજૂલ $T = 298 \,K$ લો.View Solution
- 4કોષના પ્રમાણિત $e.m.f.$ માં એક ઈલેક્ટ્રોનના પરિવર્તનથી $25°$ સે. એ$ 0.591\, V$ જોવા મળે છે. પ્રક્રિયા માટે સંતુલન અચળાંક કેટલો થાય?$ (F = 96500 C mol^{-1}; R = 8.314 JK^{-1} mol^{-1} )$View Solution
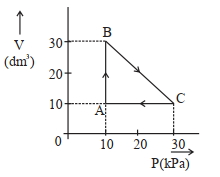
- 5$Image$ એક આદર્શ વાયુ બિંદુ $A$ થી શરૂઆત કરીને ચક્રિય સ્થાનાંતર કરે છે અને ઉપરની આકૃતિમાં દર્શાવ્યા પ્રમાણે દોરેલા પથ $\mathrm{A} \rightarrow \mathrm{B} \rightarrow \mathrm{C} \rightarrow \mathrm{A}$ દૃવારા તે જ બિંદુ પર પાછો ફરે છે. આ પ્રક્રમમાં થયેલ કુલ કાર્ય ____________$\mathrm{J}$ છે.View Solution
- 6નીચેના કયા એક સમીકરણ માટે $\Delta H^o$ પ્રક્રિયાએ નિપજના $\Delta H_f$ બરાબર હોય છે ?View Solution
- 7$CaC_2$ ઉત્પન્ન કરવા $233.0\, g$ કેલ્શિયમ ઓક્સાઇડની પૂરતા પ્રમાણમાં કાર્બન સાથે પ્રકિયા થતા કેટલા .....$kJ$ ઉષ્માનો ફેરફાર થશે ?$Ca{O_{\left( s \right)}} + 3{C_{\left( s \right)}} \to Ca{C_{2\left( g \right)}} + C{O_{\left( g \right)}}\,\,;\,\Delta {H^o} = 464.8\,kJ/mol$View Solution
- 8જો $H_2$$_{(g)}$ $+$ $Cl_2$$_{(g)}$ $\rightarrow$ $2HCl$$_{(g)}$; $\Delta$ $H = -44 \,Kcal$; $2Na$$_{(s)}$ $+ 2HCl$$_{(g)}$ $\rightarrow$ $2NaCl$$_{(s)}$ $+$ $H_2$$_{(g)}$; $\Delta$$h =$ ${-1}52\, Kcal$ તો $Na$$_{(s)}$ $+ 0.5$ $Cl_2$$_{(g)}$ $\rightarrow$ $NaCl$$_{(s)}$ ; $\Delta H$ $= ?$ ......$Kcal$View Solution
- 9જ્યારે એક મોલ હેપ્ટેન $(I)$ નું $T$ તાપમાને દહન કરવામાં આવે ત્યારે $\Delta H$ અને $\Delta U$ વચ્ચેનો તફાવત $(\Delta H - \Delta U),$ કોને સમાન થશે ?View Solution
- 10${N_{2\left( g \right)}} + 3{H_{2\left( g \right)}} \to 2N{H_{3\left( g \right)}}$ માટે $\Delta H$ = ....View Solution
