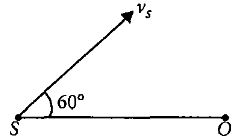
Here,
Frequency of source, \(v_{0}=100 \mathrm{Hz}\)
Velocity of source, \(v_{s}=19.4 \mathrm{ms}^{-1}\)
Velocity of sound in air, \(v=330 \mathrm{ms}^{-1}\)
As the velocity of source along the source observer line is \(v_{s} \cos 60^{\circ}\) and the observer is at rest, so the apparent frequency observed by the observer is
\({v=v_{0}\left(\frac{v}{v-v_{s} \cos 60^{\circ}}\right)}\)
\({=(100 \mathrm{Hz})\left(\frac{330 \mathrm{ms}^{-1}}{330 \mathrm{ms}^{-1}-\left(19.4 \mathrm{ms}^{-1}\right)\left(\frac{1}{2}\right)}\right)}\)
\({=(100 \mathrm{Hz})\left(\frac{330 \mathrm{ms}^{-1}}{330 \mathrm{ms}^{-1}-9.7 \mathrm{ms}^{-1}}\right)}\)
\({=(100 \mathrm{Hz})\left(\frac{330 \mathrm{ms}^{-1}}{320.3 \mathrm{ms}^{-1}}\right)=103 \mathrm{Hz}}\)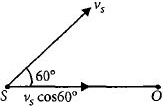
Download our appand get started for free
Similar Questions
- 1ઓરડા $A$ માટે રેવરબરેશન સમય એક સેકન્ડ છે, તો બીજા ઓરડા કે જેના બધા જ પરિમાણ ઓરડા $A$ ના પરિમાણ કરતાં બમણા હોય, તો તેના માટે રેવરબરેશન સમય (સેકન્ડમાં) કેટલો હોય?View Solution
- 2અજ્ઞાત આવૃત્તિ $250 Hz$ સાથે $8$ સ્પંદ પ્રતિ સેકન્ડ અને $270 Hz$ સાથે $12$ સ્પંદ પ્રતિ સેકન્ડ ઉત્પન્ન કરે છે.તો અજ્ઞાત આવૃત્તિ કેટલી .... $Hz$ હશે?View Solution
- 3View Solutionખેંચેલી દોરીમાં,
- 4બે સમાન પ્રકારની નળીમાં નળી $A$ એ બંને છેડેથી ખુલ્લી છે અને નળી $B$ એ એક છેડેથી બંધ છે.નળી $A$ અને નળી $B$ ની મૂળભૂત આવૃત્તિઓનો ગુણોત્તર કેટલો થાય?View Solution
- 5નીચે આપેલા પ્રગામી તરંગના સમીકરણમાંથી કયા તરંગોનો ઉપયોગ સ્થિત તરંગ ઉત્પન્ન કરવા માટે થાય?View Solution
$ {z_1} = A\sin (kx - \omega \,t) $ , $ {z_2} = A\sin (kx + \omega \,t) $ , $ {z_3} = A\sin (ky - \omega \,t) $ .
- 6બે સમાંતર દીવાલ વચ્ચે ઉભેલો માણસ તાળી પાડે ત્યારે,તેને દર સેકન્ડે પડધો સંભળાય છે,તો બે દીવાલ વચ્ચેનું અંતર કેટલું .... $m$ હશે? (હવામાં ધ્વનિની ઝડપ = $ 340 ms^{-1} $ )View Solution
- 7સ્થિર તરંગમાં નિસ્પંદ અને પ્રસ્પંદ બિંદુ વચ્ચેનું અંતર $20cm$ છે.તો $60cm$ અંતરે રહેલા બે બિંદુ વચ્ચે કળા તફાવત કેટલો થાય?View Solution
- 8View Solutionસરળ આવૃતિ તરંગમાં, સમાન કળા અને સમાન ઝડપ ધરાવતાં બે કણ વચ્ચેનું લઘુત્તમ અંતર કેટલું હોય.
- 9એક લંબગત તરંગ $y=2 \sin (\omega t-k x) cm$ વડે રજૂ થાય છે. જ્યારે તરંગવેગ કણના મહત્તમ વેગ જેટલો થાય તે માટે તરંગલંબાઈનું મૂલ્ય $...........cm$ થશે.View Solution
- 10તરંગની ગતિ $y = a\sin (kx - \omega t)$માં $y$ શેને દર્શાવે છે?View Solution
