$1.0\,\Omega $ પ્રતિ $cm$ અવરોધ ધરાવતા તારમાંથી $'A'$ શબ્દ બનાવવામાં આવે છે. આ શબ્દની બંને બાજુની લંબાઈ $20\, cm$ અને વચ્ચેના આડા ભાગની લંબાઈ $10\, cm$ છે. બે બાજુ દ્વારા બનતો ખૂણો $60$ છે. બે બાજુના ખુલ્લા છેડાં વચ્ચેનો સમતુલ્ય અવરોધ કેટલા ............ $\Omega$ થાય?
JEE MAIN 2013, Diffcult
d
For \(ADE\) \(\frac{1}{\mathrm{R}^{\prime}}=\frac{1}{2 \mathrm{x}}+\frac{1}{10}\)
For \(ADE\) \(\frac{1}{\mathrm{R}^{\prime}}=\frac{1}{2 \mathrm{x}}+\frac{1}{10}\)
or \(\quad \mathrm{R}^{\prime}=\frac{20 \mathrm{x}}{10+2 \mathrm{x}}\)
\(\mathrm{R}_{\mathrm{BC}}=\frac{20 \mathrm{x}}{10+2 \mathrm{x}}+20-\mathrm{x}+20-\mathrm{x}\) ....\((i)\)
or \(\frac{20 x}{10+2 x}+40=2 x\)
Solving we get
\(x=10\, \Omega\)
Putting the value of \(x=10\, \Omega\) in equation \(( i )\) We get
\( R_{B C} =\frac{20 \times 10}{10+2 \times 10}+20-10+20-10 \)
\(=\frac{80}{3}=26.7\, \Omega \)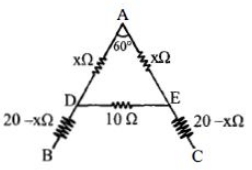
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$8 \,\Omega$ નો શંટ ધરાવતો વિદ્યુતકોષ પોટેન્શીયોમીટરના $3 \,m$ લંબાઈના તારથી સંતુલિત થાય છે. જ્યારે કોષને $4 \,\Omega$ નો શંટ લગાડવામાં આવે છે ત્યારે સંતુલિત લંબાઈ $2 \,m$ મળે છે. કોષનો આંતરિક અવરોધ ........... $\Omega$ હશે.View Solution
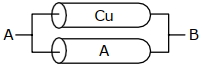
- 2આકૃતિમાં દર્શાવ્યા પ્રમાણે $25\, {cm}$ લંબાઈ અને $3\, {mm}^{2}$ આડછેદનું ક્ષેત્રફળ ધરાવતા કોપર$(Cu)$ ના સળિયાને બીજા સમાન એલ્યુમિનિયમ $(Al)$ ના સળિયા સાથે જોડેલ છે. $A$ અને $B$ બિંદુ વચ્ચેનો સમતુલ્ય અવરોધ (${m} \Omega$ માં) શોધો.View Solution
(કોપરની અવરોધકતા $=1.7 \times 10^{-8}\, \Omega \,{m}$, એલ્યુમિનિયમની અવરોધકતા $=2.6 \times 10^{-8}\, \Omega \,{m}$ લો)
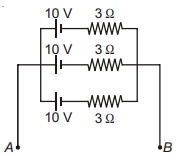
- 3$AB$ની વચ્ચે ત્રણ એકસમાન કોષોને સમાંતરમાં જોંડેલ છે. $A B$ની વચ્ચે કુલ $emf$ $..........V$ છે.View Solution
- 4એક વ્હીસ્ટન બ્રિજની ચાર ભુજાઓ $P,Q,R$ અને $S$ ના અવરોધો અનુક્રમે $10\,Ω,\,30\,Ω,\,30\,Ω $ અને $90\,Ω$ છે.કોષનો $emf $ અને આંતરિક અવરોધ અનુક્રમે $7\,V$ અને $5\,Ω $ છે.જો ગેલ્વેનોમિટરનો અવરોધ $50\,Ω $ હોય,તો કોષમાંથી નીકળતો પ્રવાહ ................ $A$ હશે.View Solution
- 5$r$ ત્રિજયાવાળા $i$ પ્રવાહધારિત તારમાં ઇલેકટ્રોનનો ડ્રિફટ વેગ $v$ છે, તો સમાન દ્રવ્ય અને અડધી ત્રિજયા ધરાવતા તારમાં $2v$ ડ્રિફટવેગ જોઇતો હોય,તો કેટલો પ્રવાહ પસાર કરવો પડે?View Solution
- 6એક અવરોધક તારનો અવરોધ $50\,^o$ સે તાપમાને $5\,\Omega$ અને $100\,^o$ સે તાપમાને $6\,\Omega$ છે. તો $0\,^o$ સે તાપમાને તેનો અવરોધ .............. $\Omega$ હશે.View Solution
- 7કોઈ પદાર્થમાંથી બનાવેલ તારને ધીમેથી ખેંચીને લંબાઇ $10\% $ વઘારવામાં આવે છે. તો નવા અવરોઘ અને અવરોઘકતા અનુક્રમે .....View Solution
- 8આપેલ નળાકાર તારની લંબાઈ $100\,\%$ જેટલી વધેલી છે. વ્યાસમાં થતાં સતત ઘટાડાને લીધે તારના અવરોધમાં થતો ફેરફાર ................ $\%$ હશે.View Solution
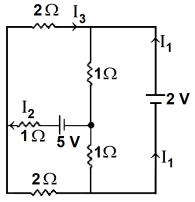
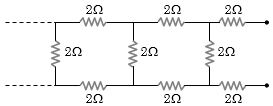
- 9View Solutionઅનંત પરિપથનો સમતુલ્ય અવરોધ .... .
- 10આપેલ પરિપથમાં પ્રવાહ $I_1$ નું મૂલ્ય $..............$ થશે.View Solution