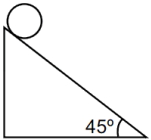
$20\;cm$ ત્રિજ્યા અને $0.5\;kg$ દળ ધરાવતી તકતી ઢાળ પર ગબડે છે. તેને ગબડવા માટે જરૂરી ઘર્ષણબળ શોધો.

AIIMS 2019, Diffcult
b
Consider the following figure.
Consider the following figure.
From the above figure,
\(Mg \sin \theta- f = ma _{ cm }\)
As we know that,
\(\tau_{ cm }= I _{ cm } \alpha\)
And,
\(f =\frac{ MR ^{2}}{2}\left(\frac{ a _{ cm }}{ R ^{2}}\right)\)
\(=\frac{ Ma _{ cm }}{2}\)
\(a_{c m}=\frac{2 f_{R}}{M}\)
Therefore,
\(mg \sin \theta- f = M \left(\frac{2 f }{ M }\right)\)
\(f =\frac{ mg \sin \theta}{3}\)
Substitute the values.
\(f =\frac{1}{2}\left(\frac{10}{3}\right)\left(\frac{1}{\sqrt{2}}\right)\)
\(=\frac{5}{3 \sqrt{2}} N\)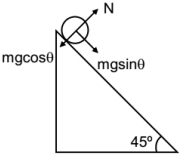
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionએક કણ નિયમિત વર્તુળાકાર ગતિ માંથી પસાર થાય છે. વર્તુળના સમતલ માં ક્યા બિંદુ એ કણનો કોણીય વેગમાન સંરક્ષિત (અચળ) હશે ?
- 2બિંદુવત દળો $1$, $2$, $ 3$ અને $4\ kg$ ના દળ અનુક્રમે બિંદુઓ $(0, 0, 0), (2, 0, 0), (0, 3, 0)$ અને $ (-2, -2, 0)$ પર રહેલા છે. આ તંત્રની $x - $ અક્ષ પર જડત્વની ચાકમાત્રા ....... $ kg - m^2$ થશે.View Solution
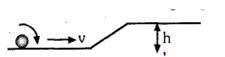
- 3ઘનગોળો ઘર્ષણ રહિત સપાટી પર રોલિંગ કરે છે. આકૃતિમાં દર્શાવ્યા પ્રમાણે સ્થાનાંતરીત વેગ $v\ \ m/s$ થી ગતિ કરીને ઢોળાવ વાળા સમતલ પર ચઢે છે. ત્યારે $v$ કેટલું હોવું જોઈએ ?View Solution
- 4કણનો સ્થાન સદીશ $\mathop r\limits^ \to = (3\hat i + 4\hat j)$ m અને કોણીય વેગ $\mathop \omega \limits^ \to = (\hat j + 2\hat k)$ $rad/sec$ હોય તો કણનો રેખીય વેગ $m/s$ માં કેટલો થાય ?View Solution
- 5નિયમિત કોણીય પ્રવેગ સાથે ભ્રમણ કરતો એક પદાર્થ શરૂ થયા પછી $5 \,s$ માં $100 \pi$ (રેડીયન) પૂર્ણ કરે છે. તો $5 \,s$ પછી તેની કોણીય ઝડપ $rev/s$ ........ $\pi$ થશે?View Solution
- 6એક પૈડાને $1000\ N-m$ નું ટોર્ક આપતા તે તેના કેન્દ્રમાંથી પસાર થતા અક્ષની આસપાસ $200\ kg-m^2$ જડત્વની ચાકમાત્રા સાથે ફરે છે. તો $3 $ સેકન્ડ પછી પૈડાનો કોણીય વેગ $=$ ......... $\ rad/s$View Solution
- 7$R$ ત્રિજ્યાની એક નિયમિત વર્તુળાકાર તકતીમાથી એક ચતુર્થ ભાગ કાપી લેવામાં આવે છે. તે ભાગનું દળ $M$ છે. મૂળ તકતીના કેન્દ્રમાથી પસાર થતી અને કાપેલા ભાગના સમતલને લંબ અક્ષ ને અનુલક્ષીને તે ભાગ ભ્રમણ કરે છે. તો તેની અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા શું હશે?View Solution
- 8સ્થિર સ્થિતિમાંથી એક રિંગ ઉપર ટૉર્ક લગાડતાં, તે અચળ કોણીય વેગ $8\ rad s^{-2}$ ની અસર હેઠળ ચાકગતિ શરૂ કરે છે. આ રિંગ $5\ s$ માં કેટલાં પરિભ્રમણ કરશે છઠ્ઠી સેકન્ડમાં આ રિંગ કેટલા પરિભ્રમણ કરશે ? જો $6\ s$ બાદ રિંગ ઉપર લાગતું ટૉર્ક શૂન્ય થઈ જાય, તો સાતમી સેકન્ડમાં આ રિંગ કેટલાં પરિભ્રમણ કરશે ?View Solution
- 9$30^o $ ના ખૂણાવાળા ઢાળ પર પોલો નળાકાર મૂકતાં $10\ m$ અંતર કાપ્યા પછી તેનો વેગ.......... $m/s$View Solution
- 10આકૃતિમાં મીટર પટ્ટીનો અડધો ભાગ લાકડાનો અને અડધો સ્ટિલનો બનેલો છે. લાકડાનો ભાગ $O$ પર કિલકિત કરેલો છે. બળ $ F$ સ્ટીલના ભાગે આપવામાં આવે છે. આકૃતિમાં $(b)$ માં સ્ટીલનો ભાગ $ O$ પર કિલકિત કરેલો છે. અને તેટલું જ લાકડાના ભાગ પર આપવામાં આવે છે.View Solution