$2a$ બાજુવાળા અને $I$ પ્રવાહધારીત વર્તુળાકાર ગુંચળાને તેનું કેન્દ્ર ઉગમબિંદુ પર રહે તેમ મૂકવામાં આવે છે. સમાન પ્રવાહ $I$ વહન કરતા લાંબા તારને $z-$અક્ષની સમાંતર અને બિંદુ $(0, b , 0),( b > > a )$ માંથી પસાર થાય તેમ મુકેલ છે. $z-$ અક્ષની દિશામાં ગુંચળા પર લાગતાં ટોર્કનું મૂલ્ય કેટલું હશે?
JEE MAIN 2020, Diffcult
a
\(F = BI 2 a =\frac{\mu_{0} I }{2 \pi r } I \times 2 a\)
\(F = BI 2 a =\frac{\mu_{0} I }{2 \pi r } I \times 2 a\)
\(F =\frac{\mu_{0} I ^{2} a }{\pi \sqrt{ b ^{2}+ a ^{2}}}\)
\(\tau= F \cos \theta \times 2 a\)
\(=\frac{\mu_{0} I^{2} a}{\pi \sqrt{b^{2}+a^{2}}} \times \frac{b}{\sqrt{b^{2}+a^{2}}} \times 2 a\)
\(\tau=\frac{2 \mu_{0} I^{2} a^{2} b}{\pi\left(a^{2}+b^{2}\right)}\)
If \(b \gg a\) then \(\tau=\frac{2 \mu_{0} I ^{2} a ^{2}}{\pi b }\)
But among the given options \((1)\) is most appropriate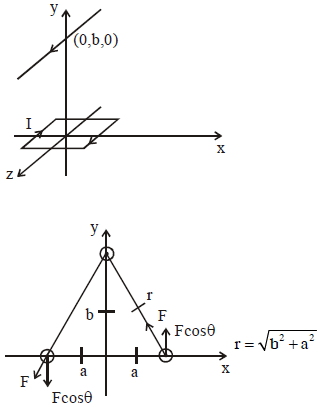
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
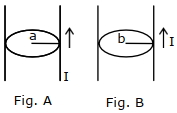
- 1આકૃતિ $A$ અને $B$ માં વર્તુળાકાર આડછેડનું ક્ષેત્રફળ ($a$ અને $b$ જ્યાં $a < b$) અને $I$ જેટલો વિદ્યુતપ્રવાહ પસાર કરતાં, કે જે આડછેદ પર સમાન રીતે વહેચાયેલો હોય તેવા બે સીધા તારો દર્શાવેલા છે. ચુંબકીય ક્ષેત્ર $B$ નું મૂલ્ય ત્રિજ્યા $r$ સાથે બદલાય છે અને તેને ........ વડે દર્શાવી શકાય છે.View Solution
- 2$L$ જેટલી સમાન લંબાઈના બે વાહક તારમાંથી એકને વાળીને વર્તુળાકાર બંધગાળો બનાવવામાં આવે છે અને બીજાને $N$ સમાન આંટાઓવાળું ગુંચળું બનાવવામાં આવે છે. જો બન્નેમાં સમાન પ્રવાહ પસાર કરાવામાં આવે તો બંધગાળાના કેન્દ્રના ચુંબકીક્ષેત્ર $(B_L)$ અને ગુચળાંના કેન્દ્રનાં ચુંબકીય ક્ષેત્ર $(B_C)$ નો ગુણોત્તર $\frac {B_L}{B_C}$ એ ______ થશે.View Solution
- 3બંનેમાંથી સમાન પ્રવાહ પસાર થતો હોય તેવા બે ગૂંચળાઓ $X$ અને $Y$ ના કેન્દ્ર આગળ અનુક્રમે ચુંબકીય ક્ષેત્રો $B_X$ અને $B_Y$ છે. જે $X$ ગૂંચળામાં આંટાની સંખ્યા $200$ અને ત્રિજ્યા $20\,cm$ અને $Y$ ગુંચળામાં આંટાની સંખ્યા $400$ અને ત્રિજ્યા $20\,cm$ છે, તો $B_X$ અને $B_Y$ નો ગુણોતર થશે.View Solution
- 4$ ({\pi ^2}) $ લંબાઇ અને $2\,A$ પ્રવાહધારિત તારથી $1\,cm$ અંતરે ચુંબકીયક્ષેત્ર $B_1$ છે.હવે તારને વર્તુળાકારમાં વાળતાં કેન્દ્ર પર ચુંબકીયક્ષેત્ર $B_2$ છે.તો $ \frac{{{B_2}}}{{{B_1}}} =$View Solution
- 5$72 \,\Omega$ અવરોધ ધરાવતા ગેલ્વેનોમીટરને $8 \,\Omega$ નો શંટ જોડતાં, કુલ પ્રવાહનો $.....$ પ્રતિશત પ્રવાહ ગેલ્વેનોમીટરમાંથી પસાર થશે.View Solution
- 6પ્રોટોનને પ્રવેગિત કરવા માટે સાઈક્લોટ્રોનનો ઉપયોગ કરવામાં આવે છે. જે કાર્યરત ચુંબકીય ક્ષેત્ર $1.0\,T$ હોય અને સાઈક્રલોટ્રોનના '$dees$' ની ત્રિજ્યા $60\,cm$ હોય તો પ્રવેગિત પ્રોટોનની ગતિ ઊર્જા $.....$ ( $MeV$ માં) હશે.View Solution
[$m _{p}=1.6 \times 10^{-27} kg , e =1.6 \times 10^{-19} C$ નો ઉપયોગ કરવો.]
- 7View Solutionઓહમના નિયમમાં એમિટર અને વૉલ્ટમીટર ને અવરોધ શ્રેણી અથવા સમાંતરમાં જોડવામાં આવે છે.
- 8સમક્ષિતિજ સાથે $30^o$ નો કોણ બનાવતા એક લીસા ઢળતાં પાટીયા પર, $0.5\; kg m^{-1}$ દ્રવ્યમાન પ્રતિ લંબાઇ ધરાવતો ધાતુનો એક સળિયો સમક્ષિતિજ રહેલો છે.આ સળિયામાં પ્રવાહ પસાર કરી ઉધર્વ દિશામાં $0.25\; T$ નું ચુંબકીયક્ષેત્ર પ્રેરિત હોય ત્યારે આ સળિયાને નીચે સરકવા દેવામાં આવતો નથી.આ સળિયાનો સ્થિર રાખવા સળિયામાં વહેતો પ્રવાહ......$A$ છે.View Solution
- 9એક વિસ્તારમાં સમાન વિદ્યુતક્ષેત્ર $\vec E$ અને સમાન ચુંબકીયક્ષેત્ર $\vec B$ એક જ દિશામાં પ્રવર્તે છે.એક ઇલેકટ્રોન આ ક્ષેત્રેની દિશામાં ચોકકસ વેગથી દાખલ થાય છે,તો...View Solution
- 10ત્રિજ્યા $=0.5\;cm$, પ્રવાહ $=1.5\, A ,$ આંટાઓ $=250,$ પરમીએબીલીટી $=700$ ધરાવતા ટોરોઈડની અક્ષ પર ચુંબકીય ક્ષેત્ર (ટેસ્લા માં) કેટલું હશે?View Solution
