$2a$ બાજુવાળા ચોરસની એક બાજુના છેડાઓ આગળ $'q'$ મૂલ્યનો બે ધન વિદ્યુતભારો મૂકેલા છે. બે સમાન મૂલ્યના ઋણ વિદ્યુતભારોને બીજા ખૂણાઓ પર મૂકેલા છે. સ્થિર સ્થિતિથી શરૂ કરીને જો વિદ્યુતભાર $Q$ એ બાજુના $1$ ના મધ્યબિંદુએથી ચોરસના કેન્દ્ર સુધી ગતિ કરે તો ચોરસના કેન્દ્ર આગળ તેની ગતિ ઊર્જા ........ છે.
AIEEE 2011, Diffcult
a
Initial potential of the charge,
Initial potential of the charge,
\(V_{A}=\frac{2 k q}{a}-\frac{2 k q}{a \sqrt{5}}\)
\(\Rightarrow V_{A}=\frac{1}{4 \pi E} \frac{2 q}{a}\left(1-\frac{1}{\sqrt{5}}\right)\)
(Here potential due to each \(q=\frac{k q}{a}\) and potential due to each \(-q=\frac{-k q}{a \sqrt{5}}\))
Final potential of the charge
\(V_{B}=0\)
( \(\because\) Point \(B\) is equidistant from all the four charges)
\(\therefore\) Using work energy theorem,
\(\left(W_{A B}\right)_{\text {electric }}=Q\left(V_{A}-V_{B}\right)\)
\(=\frac{2 q Q}{4 \pi E_{0} a}\left[1-\frac{1}{\sqrt{5}}\right]\)
\(=\left(\frac{1}{4 \pi \varepsilon_{0}}\right) \frac{2 Q q}{a}\left[1-\frac{1}{\sqrt{5}}\right]\)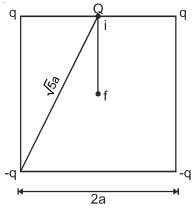
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$64$ મરક્યુરીના ટીપા દરેકને $10\, V$ સુધી વિદ્યુતભારીત કરેલ છે. તેમને ભેગા કરીને એક મોટુ બુંદ બનાવવામાં આવે છે તો આ બુંદનો વિદ્યુત સ્થીતીમાન........$V$View Solution
- 2વિદ્યુતભારીત કેપેસિટરની પ્લેટો વચ્ચેની સરેરાશ વિદ્યુતીય ઊર્જા ઘનતા (અહી $q$ = કેપેસિટર પર વિદ્યુતભાર અને $A$= કેપેસિટરની પ્લેટોનું ક્ષેત્રફળ)View Solution
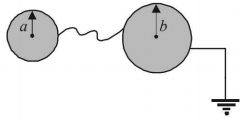
- 3$a$ અને $b$ ત્રિજ્યાના બે સુવાહક કવચને વાયર વડે જોડેલ છે. આ તંત્રની કેપેસિટી $..........$View Solution
- 4$10\, cm$ ત્રિજ્યા ધરાવતા ગોળા પર વિધુતભાર $10\,\mu \,C$ છે $20\, cm$ ત્રિજ્યા ધરાવતા વિધુતભાર વિહીન ગોળાને સંપર્કમાં લાવવામાં આવે છે તેમણે અલગ કરતાં તેમના પર પૃષ્ઠ વિધુતભાર ઘનતાનો ગુણોત્તર ............ મળેView Solution
- 5સમકેન્દ્રીય ત્રણ ગોળાકાર કવચની ત્રિજયાઓ $a,b$ અને $c\,\,(a < b < c)$ છે. આ ગોળા પરની વિદ્યુતભાર પૃષ્ઠઘનતા અનુક્રમે $\sigma ,-\;\sigma $ અને$\;\sigma \;$છે.જો $V_A,V_B$ અને $V_C$ એ કવચ પરનું વિદ્યુતસ્થિતિમાન દર્શાવતા હોય,તો $c=a+b$ માટે ____View Solution
- 6બે પ્લેટો પરનો વિદ્યુતસ્થિતિમાન અનુક્રમે $-10\, V$ અને $+ 30 \,V$ બે પ્લેટો વચ્ચેનું અંતર $2\, cm$ હોય તો તેમની વચ્ચેનું વિદ્યુત ક્ષેત્ર....$V/m$View Solution
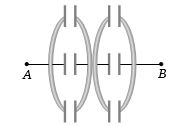
- 7$200\, V$ સહન કરી શકે તેવા $6$ કેપેસિટરને આકૃતિ મુજબ જોડેલ છે.તો $A$ અને $B$ બિંદુ વચ્ચે કેટલો મહત્તમ વોલ્ટેજ .........$V$ લગાવી શકાય?View Solution
- 8View Solutionજો નક્કર અને પોલા સુવાહક ગોળાની ત્રિજ્યા સમાન હોય તો,
- 9$Q $ વિદ્યુતભાર ધરાવતાં અને $ A $ ક્ષેત્રફળવાળા અલગ કરેલ સમાંતર પ્લેટસ કેપેસિટર $C $ ની ધાતુની પ્લેટસ વચ્ચેનું સ્થિત વિદ્યુતબળ.....View Solution
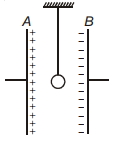
- 10View Solutionઆકૃતિમાં દર્શાવ્યા પ્રમાણે સમાંતર પૃષ્ઠ કેપેસિટરના પૃષ્ઠોની વચ્ચે અવાહક તાર વડે એક નાનો સુવાહક ગોળો લટકાવવામાં આવેલ છે. ગોળા પર લાગતું કુલ બળ કઈ દિશામાં છે?