અહી પ્રતિ મિનિટ પરિભ્રમ \(\, = \,\,120\,\,\,\,\therefore \,\) પ્રતિ સેકન્ડ પરિભ્રમન \( = \,\,\,\frac{{120}}{{60}}\,\, = \,\,2\,\,\)
\(\,\,\therefore \,\,\,\alpha \,\, = \,\, - 2\,\,rad\,{s^{ - 2}}\,,\,\,{n^2} = \,\,0\,,\,\,t\,\, = \,\,?\,,\,\,\theta \,\, = \,\,?\)
ચકગતિ ના સમીકરણ \(\omega \,\, = \,\,{\omega _{\text{0}}} + \alpha t\,\)
\(\therefore t = \frac{{\omega - {\omega _0}}}{\alpha }\,\, = \frac{{2\pi ({n_2} - {n_1})}}{\alpha }\)
અહી \(, {{\text{n}}_{\text{1}}}\) અને \({{\text{n}}_{\text{2}}}\) એ અનુક્રમે પ્રતિપ્રવેગ આપ્યા પહેલા અને પછી
પ્રતિ સેકન્ડ પરિભ્રમણો છે.
\(\therefore \,\,t = \frac{{2\pi (0 - 2)}}{{ - 2}} = 2\pi \,\) સેકન્ડ
હવે, \(\theta = {\omega _0}t + \frac{1}{2}\alpha {t^2} = (2\pi (2)) + \frac{1}{2}( - 2){(2\pi )^2}\) \((\because \,\,{\omega _0} = \,\,2\pi {n_1}\,;\,\,{n_1} = \) પરિભ્રમણ /સેકન્ડ)
હવે,\(\theta \) એકૂલ કોણીય સ્થાનાંતરછે
\(\because \,\) પરિભ્રમણોની સંખ્યા \( = \,\,\,\frac{\theta }{{2\pi }}\,\, = \,\,\frac{{4{\pi ^2}}}{{2\pi }}\,\, = \,\,2\,\pi \) પરિભ્રમણો
Download our appand get started for free
Similar Questions
- 1View Solutionએક પાતળી, સમક્ષિતિજ વર્તુળાકાર તક્તી, તેના કેન્દ્રમાંથી પસાર થતી ઊર્ધ્વ અક્ષની સાપેક્ષે ગતિ કરે છે. તક્તીની કિનારી પર એક કીટક સ્થિર સ્થિતિમાંથી તકતીના વ્યાસ પર વ્યાસના બીજા અંત્યબિંદુ તરફ ગતિ શરૂ કરે છે. કીટકની આ મુસાફરી દરમિયાન તકતીની કોણીય ઝડપ ……..
- 2$2 \,kg - m ^2$ જડત્વની ચાકમાત્રા ધરાવતાં એક ચક્રને $30 \,rad / s$ ની ઝડપે ભ્રમણ કરાવવામાં આવે છે. તેની ધાર પર લાગતું લંબબળ ચક્રને $15$ સેકંડમાં અટકાવે છે. બળનું સરેરાશ ટોર્ક ........... $N-m$ થાય?View Solution
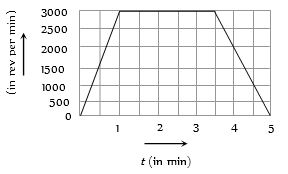
- 3View Solutionએક પ્રયોગમાં એક જેટ એંજિનનું કમ્પ્રેસર નીચે આપેલા ગ્રાફ પ્રમાણે ફરે છે તો પ્રયોગ દરમિયાન કમ્પ્રેસરના પરિભ્રમણ સંખ્યા કેટલી હોય ?
- 4View Solutionકણ ઘટતી રેખીય ઝડપથી વર્તુળમય ગતિ કરે છે, તો તેના માટે નીચેનામાંથી કયું વિધાન સાચું થાય?
- 5$R$ ત્રિજયા અને $M$ દળ ધરાવતું ડ્રમ $\theta$ ખૂણાવાળા ઢાળ પર સરક્યાં વગર ગબડે છે. ઘર્ષણ બળના કારણે .....View Solution
- 6એક ચક્ર સ્થિર સ્થિતિમાંથી શરૂ થઈને $20 \,s$ માટે $2 \,rad / s ^2$ નાં નિયમિત દરથી પ્રવેગિત થાય છે. તેને બીજી $10 \,s$ માટે એજ નિયમિત પ્રવેગ સાથે ભ્રમણ કરવાની છુટ આપવામાં આવે છે અને તે અંતે ત્યારબાદની $20 \,s$ સ્થિર થાય છે. ચક્ર દ્વારા કુલ ભ્રમણ થયેલો ખૂણો (રૂડીયનમાં) કેટલો થાય?View Solution
- 7એક હલકી મિટર સ્કેલ પર $1\,cm, 2\,cm,.........100 \,cm $ પર અનુક્રમે $1 \,g, 2\,g............ 100\, g$ વજન મૂકેલા હોય તો તંત્રને સમતોલન માં રાખવા માટે મિટર સ્કેલ ને ..... $cm$ આધાર રાખવો પડે.View Solution
- 8સમાન જડત્વની ચાકમાત્રા ધરાવતી બે તકતીઓ ની કોણીય ઝડપ ${\omega _1}\;$અને$\;{\omega _2}$છે,આ બંને તકતીઓની અક્ષ એક કરી દેવામાં આવે,તો ઊર્જાનો વ્યયView Solution
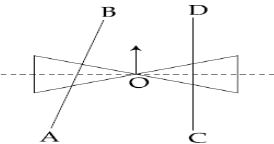
- 9બે શંકુઓને બિંદુ $O$ સાથે જોડીને એક રોલર બનાવવામાં આવેલ છે જેને બે પાટા $AB$ અને $CD$ પર અસંમિત રીતે રાખેલ છે. (જુઓ આકૃત્તિ ), રોલરની અક્ષ $CD$ ને લંબ તથા કેન્દ્ર $O$ એ $AB$ અને $CD$ ને જોડતી રેખાની મધ્યમાં છે. હલકો ધકકો દેતાં રોલર આકૃત્તિમાં બતાવ્યા પ્રમાણે ગતિ કરવાનું શરૂ કરે છે. જયાં કેન્દ્ર $O$ $ CD $ ને સમાંતર ગતિ કરે છે.આમ ગતિ કરતાં રોલરView Solution
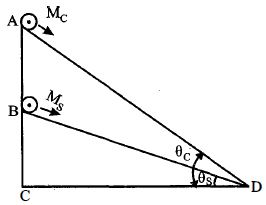
- 10આકૃતિમાં $M_c$ દળનું નળાકાર અને $M_s$ દળના ગોળાને અનુક્રમે બે ઢોળાવના બિંદુઓ $A$ અને $B$ પર મૂકેલા છે. જો તેઓ ઢોળાવ પર સરક્યાં વગર સમાન પ્રવેગથી ગતિ કરતાં હોય તો $\frac{{\sin \,{\theta _c}}}{{\sin \,{\theta _s}}}$ નો ગુણોત્તર કેટલો થાય?View Solution