$I$ જડત્વની ચાકમાત્રા ધરાવતા ચક્ર $1\ sec$ માં $n$ પરિભ્રમણ કરે છે.તેની આવૃત્તિ બમણી કરવા માટે કરવું પડતું કાર્ય
Diffcult
c
Lets consider,
Lets consider,
\(n =\) initial frequency
\(\omega=2 \pi n\)
Initial kinetic energy is
\(K _{ i }=\frac{1}{2} I \omega^2=\frac{1}{2} I \times 2 \pi n \times 2 \pi n\)
\(K _{ i }=2 I \pi^2 n ^2\)
When frequency is double to the initial frequency, the the kinetic energy will be
\(K _{ f }=\frac{1}{2} I \omega^2=\frac{1}{2} I \times 4 \pi n \times 4 \pi n\)
\(K _{ f }=8 I \pi^2 n ^2\)
By work-energy theorem,
\(W = K _{ f }- K _{ i }\)
\(W =8 I \pi^2 n ^2-2 I \pi^2 n ^2=6 I \pi^2 n ^2\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$600\, {rpm}$ ની કોણીય ઝડપથી ગતિ કરતા પદાર્થને $10\; sec$ અચળ પ્રવેગ આપતા તેની ઝડપ $1800 \,{rpm}$ થાય છે. આ પ્રક્રિયામાં થતાં પરિભ્રમણની સંખ્યા કેટલી હશે?View Solution
- 2સમાન દળ $M$ અને ત્રિજ્યા $R$ ઘરાવતો એક ઘન નળાકાર અને ઘન ગોળો $h$ ઊંંચાઈ ઘરાવતા ઢળતા ફાચર આકારના સમતલ ઉપર, ઉપરથી તળિયા તરફ ગબડે છે. નળાકારના વેગ અને ગોળાના વેગનો ગુણોત્તર $..........$ થશે.View Solution
- 3એક ઘન સમાન શંકુના શિરોબિંદુથી દ્રવ્યમાન કેન્દ્રથી અંતર $z_0$ છે.જો તેના આધારની ત્રિજયા $R$ અને ઊંચાઇ $h$ હોય,તો $z_0$ _________ બરાબર થશે.View Solution
- 4એક ગાડીના પૈડાની કોણીય ઝડપ $360 \;rpm$ થી $1200 \;rpm$ થતાં $14 \;second$ લાગે છે તો તેની કોણીય પ્રવેગ મેળવોView Solution
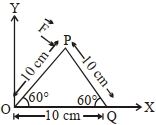
- 5આકૃતિમાં દર્શાવેલ ત્રિકોણાકાર પ્લેટ પર રહેલ $P$ બિંદુ પર $\overrightarrow{ F }=4 \hat{ i }-3 \hat{ j }$ જેટલું બળ લાગે છે. તો $P$ બિંદુ પર $O$ અને $Q$ બિંદુની સાપેક્ષે લાગતું ટોર્ક કેટલું હશે?View Solution
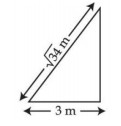
- 6$\sqrt{34} \,m$ લાંબી અને $10 \,kg$ વજન ધરાવતી એક સીડી (નીસરણી) ધર્ષણરહિત દિવાલ પર ટેક્વેલ છે. આકૃતિમાં દર્શાવ્યા પ્રમાણે તેના પગ (નીચેનો છેડો) દિવાલથી $3 \,m$ અંતરે રાખેલ છે. જો $F _{f}$ અને $F _{ w }$ એ અનુક્રમે ભોંયતળિયા અને દિવાલ દ્વારા લાગતું લંબબળ હોય તો ગુણોત્તર $F _{ w } / F _{f}$ ............ થશે.View Solution
$\left(g=10 \,m / s ^{2}\right.$ નો ઉપયોગ કરો.)
- 7એક કણનો સ્થાનસદિશ $\mathop r\limits^ \to \,\, = \,\,2\hat i\,\, - \,\,6\hat j\,\, - \,\,12\hat k$ એકમ છે. તેના પર બળ $\mathop F\limits^ \to \,\, = \,\,p\hat i\,\, + \,\,3\hat j\,\, + \,\,6\hat k$ એકમ લાગે છે, તો $ 'p'$ ના કયા મૂલ્ય માટે કોણીય વેગમાનનું સંરક્ષણ થાય ?View Solution
- 8View Solutionસમાન દળ અને સમાન દ્રવ્યમાંથી બનાવેલ ઘન ગોળો, તકતી અને ઘન નળાકારને ઢળતા સમતલ પર મૂકીને (સ્થિર સ્થિતિમાં) ગબડાવવામાં આવે, તો......
- 9બે કણો સ્થિર પડેલા છે, આંતરિક બળોના કારણે તેઓ એકબીજા તરફ ગતિ કરે છે. જો કોઈ ક્ષણે તેમની ઝડપ $v$ અને $2v$ હોય, તો તંત્રના દ્રવ્યમાન કેન્દ્રનો વેગ કેટલો થાય?View Solution
- 10નિયમિત વર્તુળાકાર ગતિ કરતા એેક કણ નો કોણીય વેગમાન $L$ છે. જો કણ ની ગતિઊર્જા બમણી કરવામાં આવે અને આવૃત્તિને અડધી કરવામાં આવે તો કોણીય વેગમાન શું બને છે ?View Solution
