$3/2$ વક્રીભવનાંક ધરાવતાં બહિર્ગોળ લેન્સની કેન્દ્રલંબાઈ $0.3\,\, m$ જેટલી છે. જો તેને $4/3$ વક્રીભવનાંક ધરાવતાં પાણીમાં ડૂબાડવામાં આવે ત્યારે લેન્સની કેન્દ્રલંબાઈ.......$cm$ માં શોધો.
Medium
c
લેન્સ મેક્સના સૂત્ર પ્રમાણે \(\frac{1}{{{f}}}\,\, = \,\,\,(\mu - 1)\,\,\left[ {\frac{1}{{{R_1}}} - \frac{1}{{{R_2}}}} \right]\) સાથે \(\mu \,\, = \,\,\frac{{{\mu _L}}}{{{\mu _M}}}\,\,\,\,\,\therefore \,\,\frac{1}{{{{{f}}_a}}}\,\, = \,\,\left[ {\frac{{(3/2)}}{1} - 1} \right]\,\,K\)
લેન્સ મેક્સના સૂત્ર પ્રમાણે \(\frac{1}{{{f}}}\,\, = \,\,\,(\mu - 1)\,\,\left[ {\frac{1}{{{R_1}}} - \frac{1}{{{R_2}}}} \right]\) સાથે \(\mu \,\, = \,\,\frac{{{\mu _L}}}{{{\mu _M}}}\,\,\,\,\,\therefore \,\,\frac{1}{{{{{f}}_a}}}\,\, = \,\,\left[ {\frac{{(3/2)}}{1} - 1} \right]\,\,K\)
અને \(\frac{1}{{{{{f}}_w}}}\, = \,\,\left[ {\frac{{(3/2)}}{{(4/3)}} - 1} \right]\,\,K\) સાથે \(K\,\, = \,\,\left[ {\frac{1}{{{R_1}}} - \frac{1}{{{R_2}}}} \right]\,\,\,\)
\( \Rightarrow \,\,\frac{{{{{f}}_w}}}{{{{{f}}_a}}}\,\, = \,\,\left[ {\frac{8}{K}} \right]\,\, \times \,\,\left[ {\frac{K}{2}} \right]\,\,\, = \,\,\,4\,\,\,\,\,\)
\(\therefore \,\,{{{f}}_w} = \,\,4\,\,\, \times \,\,0.3\,\, = \,\,1.2\,\,m\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક તરવૈયો પાણીની અંદરથી બહારની બાજુ વર્તુળાકાર ક્ષેત્રમાં જોવે છે. પાણીનો વક્રીભવનાંક $\frac{4}{3}$ અને તરવૈયાની આંખ પાણીની સપાટીથી $15\, cm$ ઊંડાઈએ છે. તો તેને બહાર દેખાતા ક્ષેત્રના વર્તુળની ત્રિજ્યા કેટલી હશે?View Solution
- 2$\sqrt 3 $ વક્રીભવનાંકના કાચના લંબચોરસ સ્લેબમાં પ્રકાશનું કિરણ $60° $ આપાત કોણે પ્રવેશે છે. તે સ્લેબમાં $5 \,cm $ અંતર કાપીને સ્લેબની બહાર નિર્ગમન પામે છે. આપાત અને નિર્ગમન કિરણ વચ્ચેનું લંબ અંતર શું થશે?View Solution
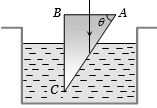
- 3આકતિમાં દર્શાવ્યા મુજબ $1.5$ વક્રીભવનાંકનો કાચનો પ્રિઝમ પાણી $(_a\mu_w = 4/3)$ માં ડૂબાડેલો છે. પ્રકાશનું પુંજ $AB$ બાજુને લંબ આપાત થઈ સંપૂર્ણ પણે $BC$ પરથી પરાવર્તન પામે છે.View Solution
- 4બર્હિગોળ લેન્સ અને અંર્તગોળ લેન્સ સંપર્કમાં છે.તેની કેન્દ્રલંબાઇનો ગુણોત્તર $2/3$ અને સમતુલ્ય કેન્દ્રલંબાઇ $30 cm$ હોય,તો લેન્સની કેન્દ્રલંબાઇ કેટલી હશે?View Solution
- 5સમક્ષિતિજ સાથે $30^\circ $નો ખૂણો બનાવતો સમતલ અરીસા પર શિરોલંબ કિરણ આપાત કરતાં અરીસા અને પરાવર્તિત કિરણ વચ્ચે ખૂણો કેટલા .....$^o$ થાય?View Solution
- 6ધારો કે બે પારદર્શક માધ્યમોને $x - z$ સમતલથી અલગ કરવામાં આવ્યા છે. $Z \geq 0$ માટે માધ્યમ $1$ નો વક્રીભવનાંક $\sqrt{2}$ અને $z <0$ માટ માધ્યમ $2$ નો વક્રીભવનાંક $\sqrt{3}$ છે. પ્રકાશનું કિરણ આ સમતલ પર આપાત થાય છે. જેનું સમીકરણ $\vec{ A }=6 \sqrt{3} \hat{ i }+8 \sqrt{3} \hat{ j }-10 \hat{ k }$ છે. માધ્યમ $-2$ માં આ કિરણ કેટલાના ખૂણે વક્રીભૂત થશે?View Solution
- 7લેન્સની વક્રતાત્રિજયા $20cm$ અને વક્રીભવનાંક $1.5$ છે.જો પ્રવાહીનો વક્રીભવનાંક $1.6$ હોય,તો તંત્રની કેન્દ્રલંબાઇ કેટલા .......$cm$ થાય?View Solution
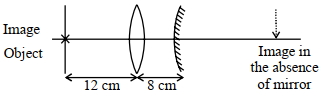
- 8એક વસ્તુને બહિર્ગોળ લેન્સથી $12 \,{cm}$ અંતરે મૂકેલો છે. આકૃતિમાં દર્શાવ્યા પ્રમાણે $15 \,{cm}$ કેન્દ્રલંબાઈ ધરાવતા બહિર્ગોળ અરિસાને લેન્સની બીજી બાજુ $8 \,{cm}$ અંતરે મૂકેલો છે. વસ્તુનું પ્રતિબિંબ વસ્તુ પાસે જ મળે છે. જ્યારે બહિર્ગોળ અરિસાને દૂર કરવામાં આવે ત્યારે વાસ્તવિક અને ઊલટું પ્રતિબિંબ મળે છે. તો વસ્તુથી આ પ્રતિબિંબ કેટલા $(cm)$ દૂર બનશે?View Solution
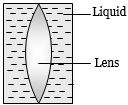
- 9View Solutionજો અજ્ઞાત દ્રવ્ય અને અજ્ઞાત કેન્દ્રલંબાઈ ધરાવતા સમતલ બહિર્ગોળ લેન્સ આપેલ હોય તો સ્ફેરોમીટરથી શું માપી શકાય?
- 10એક વસ્તુને પડદાથી $1.50\, m$ અંતરે મૂકેલ છે અને બહિર્ગોળ અરીસાને વચ્ચે મૂકવામાં આવતાં પડદા પર ચાર ગણું મોટું પ્રતિબિંબ ઉદ્દભવે છે. તો લેન્સની કેન્દ્રલંબાઈ .....$cm$ હશે.View Solution
