$[$આપેલ છે :${R}=8.31\, {~J} \,{~K}^{-1} \,{~mol}^{-1} ; \log 6.36 \times 10^{-3}=-2.19$ $\left.10^{-4.79}=1.62 \times 10^{-5}\right]$
\({K}_{700}=6.36 \times 10^{-3} {~s}^{-1}\)
\({~K}_{600}=x \times 10^{-6} {~s}^{-1}\)
\({E}_{{a}}=209 {~kJ} / {mol}\)
Applying ;
\(\log \left(\frac{{K}_{{T}_{2}}}{{~K}_{{T}_{1}}}\right)=\frac{-{E}_{{a}}}{2.303 {R}}\left(\frac{1}{{~T}_{2}}-\frac{1}{{~T}_{1}}\right)\)
\(\log \left(\frac{{K}_{700}}{{~K}_{600}}\right)=\frac{-{E}_{{a}}}{2.303 {R}}\left(\frac{1}{700}-\frac{1}{600}\right)\)
\(\log \left(\frac{6.36 \times 10^{-3}}{{~K}_{600}}\right)=\frac{+209 \times 1000}{2.303 \times 8.31}\left(\frac{100}{700 \times 600}\right)\)
\(\log \left(6.36 \times 10^{-3}\right)-\log {K}_{600}=2.6\)
\(\Rightarrow \log {K}_{600}=-2.19-2.6=-4.79\)
\(\Rightarrow {K}_{600}=10^{-4.79}\)
\(=1.62 \times 10^{-5}\)
\(=16.2 \times 10^{-6}\)
\(=x \times 10^{-6}\)
\(\Rightarrow {x}=16\)
Download our appand get started for free
Similar Questions
- 1View Solution....... ને કારણે તાપમાનમાં વધારો થવા માટે પ્રક્રિયાના દરમાં મોટો વધારો થાય છે.
- 2જો $c_o$ પ્રક્રિયકની મૂળ સાંદ્રતા હોય, તો શૂન્ય ક્રમની પ્રક્રિયા માટે અર્ધઆયુષ્ય સમય શુ થશે ?View Solution
- 3$2 \mathrm{~N}_2 \mathrm{O}_{5(\mathrm{~g})} \rightarrow 4 \mathrm{NO}_{2(\mathrm{~g})}+\mathrm{O}_{2(\mathrm{~g})}$ સમીકરણ વડે $\mathrm{CCl}_4$ માં $\mathrm{N}_2 \mathrm{O}_5$ ની વિઘટન થઈને પ્રકિયા માટે જરૂરી $\mathrm{NO}_2$ ઉત્પન્ન થાય છે. $\mathrm{N}_2 \mathrm{O}_5$ ની પ્રારંભિક સાંદ્રતા $3 \mathrm{~mol} \mathrm{~L}^{-1}$ અને તેની $30$ મિનીટ પછી $2.75 \mathrm{~mol} \mathrm{~L}^{-1}$ છે. $\mathrm{NO}_2$ બનવાનો (સર્જન) વેગ (દર) એ $x \times 10^{-3} \mathrm{~mol} \mathrm{~L}^{-1} \mathrm{~min}^{-1}$ છે. $x$ નું મુલ્ય___________ છે.(નજીકનો પૂણાંક)View Solution
- 4આપેલ આલેખ બે જુદી જુદી પ્રક્રિયા $(i)$ અને $(ii)$ માટે સમય સાથે પ્રક્રિયક $R$ ની સાંદ્રતાનો ફેરફાર રજૂ કરે છે. તી પ્રક્રિયાના ક્રમ અનુક્રમે જણાવો.View Solution
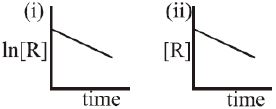
- 5પ્રક્રિયા $2A + B → A_2B $ માં જો પ્રક્રિયક $A $ ની સાંદ્રતા બમણી અને $B$ ની સાંદ્રતા અડધી કરવામાં આવેતો પ્રક્રિયાનો વેગ.....View Solution
- 6પ્રથમ ક્રમ ની પ્રકિયા માટે અચલ વેગ $2.303 \times 10^{-3} \;\mathrm{s}^{-1} .$ છે $40 \mathrm{g}$ પ્રકીયક ને $10\; \mathrm{g}$ પ્રકિયા થવા માટે લાગતો સમય........$s$View Solution
[અહી આપેલ $\left.\log _{10} 2=0.3010\right]$
- 7$H_2 + I_2 $ $\rightleftharpoons$$H_I$ પ્રક્રિયા માટે સાચો સંબંધ લખો.View Solution
- 8રાસાયણિક પ્રક્રિયાનો દર દરેક વધતા $10\,^oC$ તાપમાન માટે બમણો હોય છે. જો તાપમાન $50\,^oC$ સુધી વધે છે. તો પ્રક્રિયાનો દર કેટલા ગણો થશે?View Solution
- 9પ્રથમ ક્રમની પ્રક્રિયાનું અર્ધ-આયુષ્ય $69.35$ સેકન્ડ છે. પ્રક્રિયાના વેગ અચળાંકનું મૂલ્ય .........$\sec^{-1}$ છે.View Solution
- 10એક પ્રથમક્રમની પ્રક્રિયા માટે વેગ અચળાંક $60$ સેકન્ડ $^{-1} $ છે. પ્રક્રિયકની શરૂઆતની સાંદ્રતા $10 $ મા ભાગની થવા માટે કેટલો સમય લાગશે ?View Solution
