Let's consider a strip of thickness \(dx\) at a distance of \(x\) from the left end as shown in the figure.
\(\frac{y}{x}=\frac{d}{a}\)
\(\Rightarrow \quad y=\left(\frac{d}{a}\right) x\)
\(C_{1}=\frac{\varepsilon_{0} a d x}{(d-y)} \quad ; \quad C_{2}=\frac{k \varepsilon_{0} a d x}{y}\)
\(C_{e q}=\frac{C_{1} C_{2}}{C_{1}+C_{2}}=\frac{k \varepsilon_{0} a d x}{k d+(1-k) y}\)
Now integrating it from \(0\) to \(a\)
\(\int_0^a {\frac{{{\text{k}}{\varepsilon _0}{\text{adx}}}}{{{\text{kd}} + (1 - {\text{k}})\frac{{\text{d}}}{{\text{a}}}{\text{x}}}}} = \frac{{{\text{k}}{\varepsilon _0}{{\text{a}}^2}{\text{lnk}}}}{{{\text{d}}({\text{k}} - 1)}}\)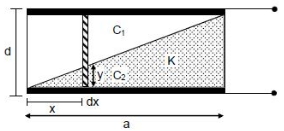
Download our appand get started for free
Similar Questions
- 1View Solutionબે સમાન અને વિરૂદ્ધ વિજભારો અને જોડતી રેખાના સમચેદી ના કોઈ પણ બિંદુ આગળ.......
- 2$d$ જેટલું પ્લેટોનું અંતર ધરાવતા કેપેસીટરને $V$ સ્થિતિમાટે રાખેલ છે. બેટરીથી છુટો કરી દીધા બાદ તેનામાં $\frac{d}{2}$ જેટલી જાડાઈનો એવો ડાઈઇલેક્ટ્રીક દાખલ કરાય છે કે જેને ડાઈઇલેકટ્ટીક અચળાંક $2$ છે. હવે તેનાં બે છેડાઓ વચ્ચે વિદ્યુત સ્થિતિમાનનો તફાવત કેટલો રહેશે ?View Solution
- 3સમાન લંબાઈની દોરીઓ વડે બે એકસમાન વિદ્યુતભારિત ગોળાઓને લટકાવવામાં આવેલા છે. દોરીઓ એકબીજા સાથે $37^{\circ}$ નો કોણ બનાવે છે. જ્યારે $0.7 \mathrm{~g} / \mathrm{cm}^3$ ની ધનતા ધરાવતા પ્રવાહીમાં અંદર લટકાવવામાં આવે છે ત્યારે કોણ સમાન રહે છે. જો ગોળાના દ્રવ્યની ધનતા $1.4 \mathrm{~g} / \mathrm{cm}^3$ હોય તો પ્રવાહીનો ડાઈઇલેકિટ્ર અચળાંક_________થશે.$\left(\tan 37^{\circ}=\frac{3}{4}\right)$View Solution
- 4View Solutionવિદ્યુત ક્ષેત્રની ઊર્જા ઘનતા કોના સમપ્રમાણમાં હોય છે?
- 5View Solutionકેપેસિટન્સનું પરિમાણિક સૂત્ર શું થાય?
- 6જો સમાંતર પ્લેટ સંધારકની પ્લેટ કે જેને બેટરી સાથે જોડવામાં આવેલ છે ને એકબીજાની નજીક ખસેડવામાં આવે છે ત્યારે. . . . . . . . .View Solution
$A$. તેમાં સંગ્રહિત વિધુતભાર વધે છે .
$B$. તેમાં સંગ્રહિત ઊર્જા ધટે છે.
$C$. તેની સંધારકતા વધે છે.
$D$. વિધુતભાર અને તેના સ્થિતિમાનનો ગુણોત્તર સમાન રહે છે.
$E$. વિધુત ભાર અને વોલ્ટેજનો ગુણાકાર વધે છે.
નીચ આપેલા વિકહ્પોમાંથી સૌથી યોગ્ય ઉતર પસંદ કરો.
- 7$1000\,V$ નો વિદ્યુતસ્થિતિમાનનો તફાવત અને $2\,mm$ અંતરે રહેલી બે પ્લેટ વચ્ચેથી ઇલેકટ્રોન પસાર થાય,ત્યારે કેટલું બળ લાગે?View Solution
- 8View Solutionખોટું વિધાન શોધો.
- 9$A$ અને $B$ બે વાહક ગોળાઓની ત્રિજ્યાઓ અનુક્રમે $1\, mm$ અને $2 \,mm$ છે અને તેઓ વિદ્યુતભારિત કરેલાં છે તથા $5\, cm$ અંતરે રાખેલા છે. હવે તેમને વાહક તારથી જોડતાં સમતોલન સ્થિતિમાં તેમની સપાટી પરનાં વિદ્યુતક્ષેત્રની તીવ્રતાઓનો ગુણોત્તર ...... છે.View Solution
- 10એક હવાવાળા સમાંતર પ્લેટ કેપેસિટરની ક્ષમતા $‘C’ $ અને બે પ્લેટો વચ્ચેનું અંતર $‘d’$ તથા વિદ્યુતસ્થિતિમાનનો તફાવત $ ‘V’ $ છે.આ હવાવાળા કેપેસિટરની પ્લેટો વચ્ચે લાગતું આકર્ષણબળ _______View Solution
