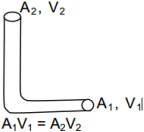
$A_{1}$ થી પ્રવાહ અંદર $3.5\, m / s$ની ઝડપથી દાખલ થઈને $A _{2}$ થી બહાર આવે છે. $A _{2}$ બિંદુથી પ્રવાહીની ઊંચાઈ ($cm$ માં) કેટલી હશે?
AIIMS 2019, Medium
Download our app for free and get started
a
Consider the following figure
Consider the following figure
Here
\(A _{1}= A _{2} soV _{1}= V _{2}=3.5 m / s\)
Use Bernoulli theorem.
\(P _{ atm }+\frac{1}{2} \rho(3.5)^{2}+\rho g (0)= P _{ atm }+\frac{1}{2} \rho(0)^{2}+\rho gh\)
\(h =\frac{(3.5 \times 3.5)^{2}}{2 g }\)
\(=0.6125 m\)
\(=61.25 cm\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1પાત્રના તળિયે $l$ લંબાઇ અને $r$ ત્રિજયા ઘરાવતી કેશનળી જોડેલ છે.તેના પર દબાણનો તફાવત $P$ હોય,ત્યારે બહાર આવતા પાણીનું કદ $V$ છે,હવે તેની સાથે શ્રેણીમાં સમાન લંબાઇ પરંતુ અડધી ત્રિજયા ધરાવતી કેશનળી જોડતાં બહાર આવતાં પ્રવાહીનું કદ ( તંત્ર વચ્ચે દબાણનો તફાવત $P$ છે. )View Solution
- 2$1$ મી પાણી ભરેલા પાત્રમાં તળીયેથી $0.25$ મી અંતરે છિદ્ર પાડતાં તેની અવધિ ...... (સેમી માં)View Solution
- 3કોઈ સમતલીય પ્લેટ ${v_1}$ જેટલી સામાન્ય ઝડપે એક નિયમિત આડછેદ વાળા હવાઈ જહાજ તરફ ગતિ કરે છે. હવાઈ જહાજ કદ $V$ પ્રતિ સેકન્ડ ના દરે અને ${v_2}$ વેગથી પાણી છોડે છે.પાણી ની ઘનતા $\rho $ છે. ધારો કે પાણી નો છંટકાવ પ્લેટ ની સપાટી પર કાટખૂણે થાય છે. તો હવાઈ જહાજ ના પાણી દ્વારા પ્લેટ પર લાગતું બળ કેટલું હશે?View Solution
- 4પાત્રના તળિયે $1 \,cm^{2}$ આડછેદવાળું છિદ્ર છે,પાત્રમાં $70\, cm^{3}/sec$ ના દરથી પાણી નાખતાં મહત્તમ ........ $cm$ ઊંચાઇ સુઘી પાણી ભરી શકાય.View Solution
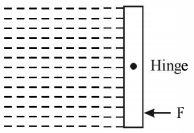
- 5$1\,m \times 1\,m$ $size$ નો ચોરસ ગેટ તેના મધ્યબિંદુથી લટકાવેલ છે.$\rho$ ઘનતાનું પ્રવાહી ગેટની ડાબી બાજુની જગ્યામાં ભરેલ છે. તો ગેટને સ્થિર રાખવા માટે જોઈતું બળ $F . \ldots . .. ....$View Solution
- 6એક નિયમિત આડ-છેદની શિરોલંબ $U-$ટ્યૂબએે બંને ભૂજામાં પાણી ધરાવે છે. કોઈ પણ એક ભૂજા પર $10 \,cm$ ની ગ્લિસરીન સ્તંભ ઉમેરવામાં આવે છે. ($R.D. = 1.2$) બંને ભૂજામાં બંને મુક્ત સપાટીઓ વચ્ચેના સ્તરનું તફાવત ........ $cm$ હશે ($R.D =$ સાપેક્ષ ધનતા)View Solution
- 7ગુરુત્વાકર્ષણની અસર હેઠળ મુક્ત પતન કરાવવામાં આવે અને તે પાણીની ટાંકીમાં દાખલ થાય તે પહેલાં ' $h$ ' જેટલું અંતર કાપે છે. જો પાણીમાં દાખલ થયા બાદ તેનો વેગ બદલાતો ન હોય, તો $h$ નું સંનિક્ટ્ટ મૂલ્ચ ....... થશે. (પાણી માટે સ્નિગધતા $9.8 \times 10^{-6} \mathrm{~N}-\mathrm{s} / \mathrm{m}^2$ લો.)View Solution
- 8તળાવના તળિયેથી પરપોટો સપાટી પર આવતા ત્રિજયા બમણી થાય છે. $H$ ઊંચાઇના પાણીના સ્તંભનું દબાણ વાતાવરણ જેટલું હોય,તો તળાવની ઊંડાઇ કેટલી થાય? ( પ્રક્રિયા સમતાપી ધારો )View Solution
- 9$0.5\,m$ લંબાઈ ધરાવતો ઘન પાણી પર તરે છે જેનું $30\%$ કદ પાણીની અંદર છે. બ્લોક પર મહત્તમ ......$kg$ વજન મૂકી શકાય કે જેથી તે સંપૂર્ણ પાણીમાં ડૂબી ના જાય. [પાણીની ઘનતા $= 10^3\,kg/m^3$ ]View Solution
- 10$H$ ઊંચાઈ અને $\rho$ ઘનતા ધરાવતા ટેન્કમાં પ્રવાહી ભરવામાં આવે છે. તો આ કન્ટેનરની દીવાલ પર લાગતું સરેરાશ દબાણ.View Solution