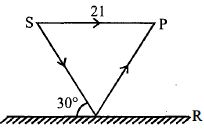
આકૃતિમાં દર્શાવ્યા પ્રમાણે ઉદગમ $S$ માંથી નિકળતા બે કિરણના સંપાતિકરણથી બિંદુ $P$ આગળ વ્યતિકરણની ભાત જોવા મળે છે. તો બિંદુ $P$ આગળ મળતી મહત્તમ તીવ્રતા $I$ નું મૂલ્ય કેટલું હશે? ($R$ એ સંપૂર્ણ પરાવર્તિક સપાટી છે)

JEE MAIN 2014, Diffcult
c
From the figure straight path \(\mathrm{SP}=2 l\)
From the figure straight path \(\mathrm{SP}=2 l\)
Reflected path \(\mathrm{SP}=2 l\) sec \(30^{\circ}\)
So path difference is \(2 l\left(\sec 30^{\circ}-1\right)\)
Also the ray, when reflected by the mirror, suffers a phase change of \(\pi\)
So the total difference in phase is \(2 l\left(\sec 30^{\circ}-1\right) \times \frac{2 \pi}{\lambda}+\pi\)
For constructive interference
\(2 l\left(\sec 30^{\circ}-1\right) \times \frac{2 \pi}{\lambda}+\pi=2 n \pi\)
Solving this, we get \(l=\frac{(2 n-1) \lambda \sqrt{3}}{4(2-\sqrt{3})}\)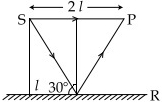
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionકેટલીક ચલણી નોટોને ત્રાસી કરીએ તેમ તેનો રંગ બદલાય છે (નકલી નોટોથી દૂર રહેવા માટે) આ શાના કારણે હોય છે?
- 2કોઈ એક તારમાંથી $600\, nm$ તરંગલંબાઈનો પ્રકાશ આવે છે તેમ ધારો. $2 \;m$ વ્યાસના ઓબ્જેક્ટિવ ધરાવતા ટેલિસ્કોપની વિભેદન સીમા $....... \times 10^{-7}\; rad$ છે.View Solution
- 3યંગના પ્રયોગમાં બે સ્લિટ વચ્ચેનું અંતર $0.2\,mm$ છે અને પડદો આ બંને સ્લિટથી $200\, cm$ દૂર છે. પ્રકાશની તરંગલંબાઈ $5000 \,Å$ હોય, તો ત્રીજી પ્રકાશિત શલાકાનું મધ્યસ્થ શલાકાના મધ્યબિંદુથી અંતર.......$cm$ શોધો.View Solution
- 4View Solutionબિંદુવત ઉદ્ગમના તરંગઅગ્ર કેવા આકારના હોય?
- 5યંગના ડબલ સ્લીટના વ્યતિકરણના પ્રયોગમાં સ્લીટની પહોળાઈનો ગુણોત્તર $1 : 25$. હોય તો વ્યતિકરણની ભાતમાં મળતી મહત્તમ અને ન્યૂનતમ તીવ્રતાનો ગુણોત્તર કેટલો મળે?View Solution
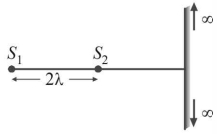
- 6બે સ્ત્રોતને $2 \lambda$ જેટલા અંતરે રાખેલ છે. એક મોટી સ્ક્રીન તેમનો જોડતી રેખાથી લંબ છે. ( $\lambda=$ પ્રકાશની તરંગલંબાઈ) સ્ક્રીન પરના મહત્તમની સંખ્યા ........View Solution
- 7બે સુસમ્બદ્વ ઉદ્ગમોની તીવ્રતાનો ગુણોત્તર $\alpha $ છે.$\frac{{{I_{max}} - {I_{min}}}}{{{I_{max}} + {I_{min}}}}$ નું મૂલ્ય કેટલું થાય?View Solution
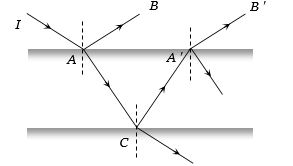
- 8દરેક પ્લેટ $25\%$ આપાત પ્રકાશની તીવ્રતાનું પરાવર્તન કરે છે. જયારે $AB$ અને $A'B'$ ને યંગના પ્રયોગની બે સ્લિટ લેવામાં આવે તો મહતમ અને ન્થૂનતમ તીવ્રતાનો ગુણોતર $ \frac {I_{\max }}{I_{\min }} $ કેટલો થાય?View Solution
- 9એક સ્લીત ના પ્રયોગમાં થતાં વિવર્તનમાં સફેદ પ્રકાશ વડે $a$ પહોળાયની સ્લીટને પ્રકાશિત કરવામાં આવે છે. લાલ પ્રકાશ ($\lambda = 6500\;\mathring A$) માટે પ્રથમ લઘુત્તમ $\theta = {30^o}$ ખૂણે મળે છે. તો $a$ નું મૂલ્ય કેટલું હશે?View Solution
- 10યંગના પ્રયોગમાં $P$ બિંદુએ તીવ્રતા મહતમ તીવ્રતાથી ચોથા ભાગની છે.પ્રકાશની તરંગલંબાઇ $\lambda$ અને બે સ્લિટ વચ્ચેનું અંતર $ d$ છે.$P$ અને મઘ્યસ્થ અઘિકતમ વચ્ચેનું કોણીય અંતર કેટલું થાય?View Solution
