યંગના ડબલ સ્લીટના વ્યતિકરણના પ્રયોગમાં સ્લીટની પહોળાઈનો ગુણોત્તર $1 : 25$. હોય તો વ્યતિકરણની ભાતમાં મળતી મહત્તમ અને ન્યૂનતમ તીવ્રતાનો ગુણોત્તર કેટલો મળે?
AIEEE 2012, Diffcult
c
We know that,
We know that,
\(\frac{{{I_{\max }}}}{{{I_{\min }}}} = \frac{{{{\left( {\sqrt {\frac{{{\omega _1}}}{{{\omega _2}}} + 1} } \right)}^2}}}{{{{\left( {\sqrt {\frac{{{\omega _1}}}{{{\omega _2}}} - 1} } \right)}^2}}}\)
\(I_{\max }\) and \(I_{\min }\) are maximum and minium intensity
\(\omega_{1}\) and \(\omega_{2}\) are widths of two slits
\(\therefore \,\,\frac{{{I_{\max }}}}{{{I_{\min }}}} = \frac{{{{\left( {\sqrt {\frac{1}{{25}}} + 1} \right)}^2}}}{{{{\left( {\sqrt {\frac{1}{{25}}} - 1} \right)}^2}}}\) \(\left( {\frac{{{\omega _1}}}{{{\omega _2}}} = \frac{1}{{25}}\operatorname{given} } \right)\)
On solving we get,
\(\frac{{{I_{\max }}}}{{{I_{\min }}}} = \frac{{\frac{{36}}{{25}}}}{{\frac{{16}}{{25}}}} = \frac{9}{4} = 9:4\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1યંગના બે સ્લિટના પ્રયોગમા પથ તફાવત $\frac{\lambda}{6}$ છે તે બિંદુએ તીવ્રતા $I$ છે તો મહતમ તીવ્રતાને $I_0$ વડે દર્શાવવામા આવે તો, $\frac{I}{I_0}$.View Solution
- 2યંગના ડબલ -સ્લિટના પ્રયોગમાં બંને સ્લિટ એકબીજાથી $2\; mm$ દૂર છે અને તે $\lambda_1= 12000\;\mathring A$ અને $ \lambda_2= 10000\;\mathring A$ એમ બે તરંગલંબાઇવાળા ફોટોન્સથી પ્રકાશિત કરવામાં આવે છે. સ્લિટથી $ 2\; m$ અંતરે રહેલા પડદા પર સામાન્ય મઘ્યસ્થ પ્રકાશિત શલાકાથી કયા લઘુતમ અંતર ($mm$ માં) માટે એક વ્યતિકરણ ભાતની પ્રકાશિત શલાકા અને બીજા પ્રકાશિત શલાકા એકબીજા પર સંપાત થશે?View Solution
- 3View Solutionવિર્વતનમાં લાલ પ્રકાશની બદલે જાંબલી પ્રકાશ વાપરતા
- 4એક સ્લીટને $\lambda$ જેટલી તરંગલંબાઈ ધરાવતા તરંગના પથ પર મૂકવામાં આવે છે. તો મુખ્ય મહત્તમની કોણીય પહોળાઈ ....View Solution
- 5યંગના પ્રયોગમાં સફેદ પ્રકારનો ઉપયોગ કરવામાં આવે છે. બે સ્લિટ વચ્ચેનું અંતર $b$ છે.સ્લિટ અને પડદા વચ્ચે નું અંતર $d (d>> b)$ છે. સ્લિટની બરાબર સામે ગેરહાજર તરંગલંબાઈView Solution
- 6એક માધ્યમ માટે ધ્રુવીભવન કોણ $60^o$ હોય,તો તેના માટે ક્રાંતિકોણ કેટલો થાય?View Solution
- 7$286\, kms ^{-1}$ ની ઝડપે પૃથ્વીથી દૂર ગેલેક્સી ગતિ કરે છે $630\, nm$ તરંગલંબાઈમાં શિફ્ટ $x \times 10^{-10}\, m$ હોય તો $x=.............$View Solution
- 8View Solutionયંગના બે સ્લીટના પ્રયોગમાં જો આપેલ બે સ્લીટના પ્રકાશમાં શરૂઆતનો કોઈ કળા તફાવત ના હોય, તો પાંચમા ન્યૂનતમ પાસે કેટલો કળા તફાવત હશે?
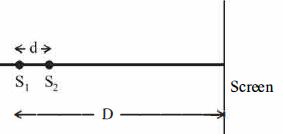
- 9આકૃતિમાં દર્શાવ્યા પ્રમાણે બે સુસમ્બદ્ધ ઉદ્ગમો $S_1$ અને $S_2$ ખૂબ નાના અંતર $ ‘d’$ થી અલગ કરેલા છે.પડદા પર ઉત્પન્ન શલાકાઓ _____ હશે.View Solution
- 10View Solutionવ્યતિકરણમાં બે ઉદગમ કેવા હોવા જોઈએ.
