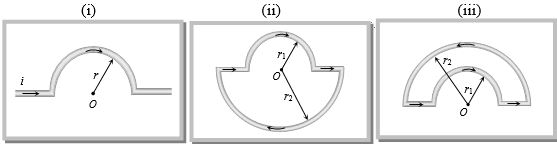
| $(i)$ | $(ii)$ | $(iii)$ |
| (A) $\frac{{{\mu _0}i}}{r}$ $\otimes$ | (A) $\frac{{{\mu _0}i}}{4}\left( {\frac{1}{{{r_1}}} - \frac{1}{{{r_2}}}} \right)$ $\otimes$ | (A) $\frac{{{\mu _0}i}}{4}\left( {\frac{1}{{{r_1}}} - \frac{1}{{{r_2}}}} \right)$ $\otimes$ |
| (B) $\frac{{{\mu _0}i}}{{2r}}$ $\odot$ | (B) $\frac{{{\mu _0}i}}{4}\left( {\frac{1}{{{r_1}}} + \frac{1}{{{r_2}}}} \right)$ $\otimes$ | (B) $\frac{{{\mu _0}i}}{4}\left( {\frac{1}{{{r_1}}} + \frac{1}{{{r_2}}}} \right)$ $\otimes$ |
| (C) $\frac{{{\mu _0}i}}{{4r}}$ $\otimes$ | (C) $\frac{{{\mu _0}i}}{4}\left( {\frac{1}{{{r_1}}} - \frac{1}{{{r_2}}}} \right)$ $\odot$ | (C)$\frac{{{\mu _0}i}}{4}\left( {\frac{1}{{{r_1}}} - \frac{1}{{{r_2}}}} \right)$ $\odot$ |
| (D) $\frac{{{\mu _0}i}}{{4r}}$ $\odot$ | (D) $0$ | (D) $0$ |
\((i)\) \((c)\) \(B_1 = B_3 = 0\)
\({B_2} = \frac{{{\mu _0}}}{{4\pi }}.\frac{{\pi i}}{r}\) \(\otimes\)
\({B_{net}} = {B_1} + {B_2} + {B_3} = \frac{{{\mu _0}}}{{4\pi }}.\frac{{\pi \,i}}{r}\) \(\otimes\) \(⇒\) \({B_{net}} = \frac{{{\mu _0}i}}{{4r}} \otimes \)
\((ii)\) \((b)\) \(B_1 = B_3 = 0\)
\({B_2} = \frac{{{\mu _0}}}{{4\pi }}.\frac{{\pi \,i}}{{{r_1}}} \otimes \)
\({B_4} = \frac{{{\mu _0}}}{{4\pi }}.\frac{{\pi \,i}}{{{r_2}}} \otimes \)
So, \({B_{net}} = {B_2} + {B_4} = \frac{{{\mu _0}}}{{4\pi }}.\pi \,i\left( {\frac{1}{{{r_1}}} + \frac{1}{{{r_2}}}} \right) \otimes \)
\((iii)\) \((a)\) \(B_1 = B_3 = 0\)
\({B_2} = \frac{{{\mu _0}}}{{4\pi }}.\frac{{\pi \,i}}{{{r_1}}} \otimes \)
\({B_4} = \frac{{{\mu _0}}}{{4\pi }}.\frac{{\pi \,i}}{{{r_2}}} \otimes \) \(|{B_2}|\,\, > \,\,|{B_4}|\)
\({B_{net}} = {B_2} - {B_4} \Rightarrow {B_{net}} = \frac{{{\mu _0}i}}{4}\left( {\frac{1}{{{r_1}}} - \frac{1}{{{r_2}}}} \right) \otimes \)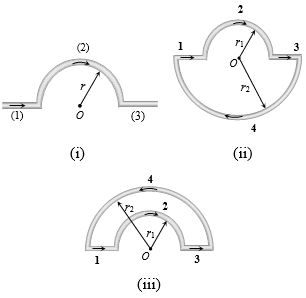
Download our appand get started for free
Similar Questions
- 1$80 \,cm$ લંબાઈના એક સોલેનોઈડ પર પાસ-પાસે દરેક $400$ આંટા વાળા $5$ આવરણ વિંટાળ્યા છે. સોલેનોઈડનો વ્યાસ $1.8 \,cm$ છે. જો સોલેનોઈડમાં $8.0 \,A$ વિદ્યુતપ્રવાહ વહેતો હોય, તો તેના કેન્દ્ર પાસે $B$ નું મૂલ્ય શોધો.View Solution
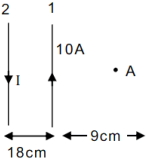
- 2બે અનંત લંબાઈના તારમાંથી પ્રવાહ પસાર થાય છે, $A$ બિંદુ આગળ ચુંબકીયક્ષેત્ર શૂન્ય હોય તો પ્રવાહ $I=.....$ ($A$ માં)View Solution
- 3$1\, T$નું ચુંબકીય ક્ષેત્ર ધરાવતા સાઈકલોટ્રોનની આવૃતિ .....View Solution
- 4$2.0\,eV$ ની ગતિઊર્જા ધરાવતો પ્રોટોન $\frac{\pi}{2} \times 10^{-3}\,T$ ના સમાન ચુંબકીય ક્ષેત્રમાં ગતિ કરે છે. ચુંબકીય ક્ષેત્રની દિશા અને પ્રોટોનના વેગ વચ્ચેનો ખૂણો $60^{\circ}$ છે. પ્રોટોન દ્વારા લેવામાં આવેલા હેલિકલ પથની પિચ .......... $cm$ છે (પ્રોટોનનું દળ $=1.6 \times 10^{-27}\,kg$ અને પ્રોટોન પરનો વિદ્યુતભાર $ =1.6 \times 10^{-19}\,kg$ લો,)View Solution
- 5$L$ લંબાઇ અને $I$ પ્રવાહધારિત તારને વર્તુળમાં વાળતાં ચુંબકીય મોમેન્ટ કેટલું થાય?View Solution
- 6$r$ ત્રિજ્યાની એક વર્તુળાકાર સુવાહક રીંગમાંથી અચળ વિદ્યુતપ્રવાહ $i$ પસાર થાય છે. તેને એકરૂપ ચુંબકીય ક્ષેત્ર $B$માં મૂકવામાં આવ્યો છે કે જેથી $B$ રિંગના સમતલને લંબ છે. રીંગ પર લાગતું કુલ ચુંબકીય બળ કેટલું છે ?View Solution
- 7જ્યારે બે ગુંચળામાંથી સમાન વિદ્યુત પ્રવાહ પસાર થાય છે. ત્યારે તેના કેન્દ્ર પાસે સમાન ચુંબકીય ક્ષેત્ર ઉત્પન્ન થાય છે. જો ગૂંચળાઓમાં આંટાઓની સંખ્યાનો ગુણોતર $8 : 15$ હોય,તો તેની ત્રિજ્યાનો ગુણોત્તર કેટલો હશે ?View Solution
- 8$a$ ત્રિજયાના પ્રવાહધારીત ગુંચળાના કેન્દ્ર અને અક્ષના કેન્દ્રથી $r$ અંતરે રહેલા બિંદુ પાસેની ચુંબકીયક્ષેત્રની તીવ્રતામાં થતો આંશિક ફેરફાર કેટલો હશે? $(r << a$ લો$)$View Solution
- 9એક રેડિયોએક્ટિવ પદાર્થ દ્વારા ઉત્સર્જતો કણ ચુંબકીયક્ષેત્રમાં વિચલન અનુભવે છે તો કણ કયો હશે?View Solution
$(i)$ ઇલેક્ટ્રોન $(ii)$ પ્રોટોન $(iii)$ $H{e^{2 + }}$ $(iv)$ ન્યૂટ્રોન
- 10$2000 $ આંટા અને $1.5 \times 10^{-4}\ m^2$ આડછેદનું ક્ષેત્રફળ ધરાવતો સોલેનોઇડ $2\ A $ પ્રવાહનું વહન કરે છે. સોલેનોઇડને કેન્દ્ર પર અને તેની લંબાઈને લંબ દોરી વડે લટકાવેલ છે કે જેથી તે $5 \times 10^{-2} \;T $ ચુંબકીયક્ષેત્રમાં તેની અક્ષ સાથે $ 30^o$ ના ખૂણે સમક્ષિતિજ સમતલમાં ફરી શકે. સોલેનોઇડ પર લાગતું ટોર્ક કેટલું હશે?View Solution
