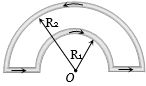
આપેલ પરિપથમાં કેન્દ્ર $O$ પર ચુંબકીયક્ષેત્ર કેટલું થાય?

IIT 1988, Diffcult
a
(a) In the following figure, magnetic fields at \(O\) due to sections \(1\), \(2\), \(3\) and \(4\) are considered as \({B_1},\,{B_2},\,{B_3}\) and \({B_4}\) respectively.
\({B_1} = {B_3} = 0\)
\({B_2} = \frac{{{\mu _0}}}{{4\pi }}.\frac{{\pi \,i}}{{{R_1}}} \otimes \)
\({B_4} = \frac{{{\mu _0}}}{{4\pi }}.\frac{{\pi \,i}}{{{R_2}}} \odot\) As \(|{B_2}|\,\, > \,\,|{B_4}|\)
So \({B_{net}} = {B_2} - {B_4} \Rightarrow {B_{net}} = \frac{{{\mu _0}i}}{4}\left( {\frac{1}{{{R_1}}} - \frac{1}{{{R_2}}}} \right) \otimes \)
(a) In the following figure, magnetic fields at \(O\) due to sections \(1\), \(2\), \(3\) and \(4\) are considered as \({B_1},\,{B_2},\,{B_3}\) and \({B_4}\) respectively.
\({B_1} = {B_3} = 0\)
\({B_2} = \frac{{{\mu _0}}}{{4\pi }}.\frac{{\pi \,i}}{{{R_1}}} \otimes \)
\({B_4} = \frac{{{\mu _0}}}{{4\pi }}.\frac{{\pi \,i}}{{{R_2}}} \odot\) As \(|{B_2}|\,\, > \,\,|{B_4}|\)
So \({B_{net}} = {B_2} - {B_4} \Rightarrow {B_{net}} = \frac{{{\mu _0}i}}{4}\left( {\frac{1}{{{R_1}}} - \frac{1}{{{R_2}}}} \right) \otimes \)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$a$ બાજુવાળા ચોરસ તારની ફ્રેમમાં $i$ પ્રવાહ પસાર થતાં કેન્દ્ર પર ચુંબકીયક્ષેત્ર કેટલું થાય?View Solution
- 2$m$ દળ અને $Q$ વિદ્યુતભાર અને $K$ ગતિઊર્જા ધરાવતો કણ એકસમાન ચુંબકીયક્ષેત્રમાં લંબરૂપે દાખલ થાય છે.તો $ 3 \,sec $ પછી ગતિઊર્જા......$K$ થાય.View Solution
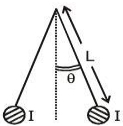
- 3$I$ વિદ્યુતપ્રવાહ ધરાવતા બે પાતળા લાંબા વિદ્યુતભારિત તારને $L$ લંબાઇની અવાહક દોરીઓ વડે ટેકવવામાં આવ્યા છે,કે જેથી તેઓ આકૃતિમાં દર્શાવ્યા મુજબ સંતુલન સ્થિતિમાં રહે.અત્રે દોરીઓ ઊર્ધ્વદિશા સાથે ‘$\theta '$ કોણ બનાવે છે.જો તાર માટે એકમ લંબાઇ દીઠ સરેરાશ $‘λ’$ હોય,તો પ્રવાહ $I$ નું મૂલ્ય _______. ( $ g$ $=$ ગુરુત્વપ્રવેગ)View Solution
- 4એક ગેલ્વેનોમીટરને $200 \Omega$ નો અવરોધ અને તે $20 \mu \mathrm{A}$ પ્રવાહ માટે પૂર્ણ સ્કેલ આવર્તન આપે છે. તેને $(0-20) \mathrm{mA}$ ની રેન્જ (ગોળા)ના એમીટર તરીકે વાપરવું હોય તો તેમાં ઉમેરવો પડતો અવરોધ ......... થશે.View Solution
- 5$40\,g$ દળ અને $50\,cm$ લંબાઈ ધરાવતા એક સુરેખ તાર $AB$ ને આકૃતિમાં દર્શાવ્યા પ્રમાણે લચીલા લેડનાં જોડકાં સાથે $0.40\,T$ નાં મૂલ્ય ધરાવતા સમાન યુંબકીય ક્ષેત્રમાં લટકાવવામાં આવે છે. લેડના આધાર પર લાગતા તણાવને દૂર કરવા માટે ........... $A$ મૂલ્યનો વીજપ્રવાહ લાગશે. ($g =10\,ms ^{-2}$ લો)View Solution
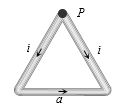
- 6$'a' $ બાજુવાળા સમબાજુ ત્રિકોણમાં $i $ પ્રવાહનું વહન થાય છે.ત્રિકોણના બિંદુ $P$ પર ચુંબકીયક્ષેત્ર કેટલું થાય?View Solution
- 7View Solutionચુંબકીય ક્ષેત્રમાં પ્રવાહ ગુંચળું ...........
- 8આકૃતિ $A$ અને $B$ માં વર્તુળાકાર આડછેડનું ક્ષેત્રફળ ($a$ અને $b$ જ્યાં $a < b$) અને $I$ જેટલો વિદ્યુતપ્રવાહ પસાર કરતાં, કે જે આડછેદ પર સમાન રીતે વહેચાયેલો હોય તેવા બે સીધા તારો દર્શાવેલા છે. ચુંબકીય ક્ષેત્ર $B$ નું મૂલ્ય ત્રિજ્યા $r$ સાથે બદલાય છે અને તેને ........ વડે દર્શાવી શકાય છે.View Solution
- 9એક વર્તુળાકાર વિદ્યુતપ્રવાહધારિત ગુંચળાની ત્રિજ્યા $R$ છે. ગુંચળાના કેન્દ્રથી તેની અક્ષ પર કેટલા અંતરે ચુંબકીયક્ષેત્રની તીવ્રતા તેના કેન્દ્ર પરની તીવ્રતા કરતા $\frac{1}{2 \sqrt{2}}$ ગણી હશે?View Solution
- 10$d$ અંતરે રહેલા બે લાંબા સમાંતર તારમાંથી પસાર થતા પ્રવાહ $I_1$ અને $I_2$ છે.બંને પ્રવાહ એક જ દિશામાં હોય,તો તાર વચ્ચે લાગતું બળ $F$ છે.હવે એક પ્રવાહનું મૂલ્ય બમણું અને દિશા વિરુધ્ધ કરવામાં આવે છે.બંને તારને $3\,d$ અંતરે મૂકતાં નવું બળ કેટલું થશે?View Solution
