આરંભમાં જયારે વાયુનું દબાણ $500 \,torr$ હોય ત્યારે વાયુમય સંયોજન $A$ નો વિધટન માટે અર્ધઆયુષ્ય $240\, s$ છે. જ્યારે દબાણ $250 \,torr$ હોય ત્યારે અર્ધ આયુષ્ય $4.0 \,min$ મળે છે. તો પ્રક્રિયાક્રમ $........$ છે. (નજીકના પૂર્ણાંકમાં)
JEE MAIN 2022, Medium
Download our app for free and get started
d
$\left( t _{1 / 2}\right)_{500 \text { torr }}=240\,sec =4\,min$.
$\left( t _{1 / 2}\right)_{500 \text { torr }}=240\,sec =4\,min$.
$\left( t _{1 / 2}\right)_{250 \text { torr }}=4\,min$
$t _{1 / 2} \propto a ^{1- n }$
As $t _{1 / 2}$ is independent of initial pressure. Hence, order is $1^{st}$ order.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1રાસાયણિક પ્રકિયા ની સક્રિયકરણ ર્જા $(E_a)$ અને અચળ વેગ $(k_1$ અને $ k_2)$ બે જુદા જુદા તાપમાને પ્રક્રિયા $(T_1$ અને $T_2)$ કોના દ્વારા સંબંધિત છેView Solution
- 2View Solutionનીચેનામાંથી કયો આલેખ સક્રિયકરણ ઊર્જાનું મૂલ્ય આપણને આપે છે?
- 3એઝોમિથેનના વિધટન માટે,View Solution
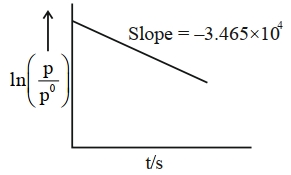
$CH _3 N _2 CH _3( g ) \rightarrow CH _3 CH _3( g )+ N _2( g )$
આ એક પ્રથમક્રમ પ્રક્રિયા છે. $600\, K$ પર સમય સાથે આંશિક દબાણમાં વિવિધતા નીચે આપેલ છે. પ્રક્રિયાનો અર્ધ આયુષ્ય $\times 10^{-5}\, s$ છે. [નજીકનો પૂર્ણાંક]
- 4View Solutionનીચેનામાંથી કયો આલેખ સક્રિયકરણ ઊર્જાનું મૂલ્ય આપણને આપે છે?
- 5નીચેની પ્રક્રિયા $2A + B \rightarrow C + D - $ માટે લાગુ પડતાં નિયમ પસંદ કરો.View Solution
$1$. $[A]$ $0.1$, $[B]$ $0.1 - $ પ્રારંભિક દર $ \rightarrow 7.5 \times 10^{-3}$
$2$. $[A]$ $0.3$, $[B]$ $0.2 -$ પ્રારંભિક દર $ \rightarrow 9.0 \times 10^{-2}$
$3$. $[A]$ $0.3$, $[B]$ $0.4 -$ પ્રારંભિક દર $ \rightarrow 3.6 \times 10^{-1}$
$4$. $[A]$ $0.4$, $[B]$ $0.1 -$ પ્રારંભિક દર $ \rightarrow 3.0 \times 10^{-2}$
- 6View Solutionપ્રદિપ્તીનુ બુઝાવુ ........ પર આધાર રાખે છે.
- 7નીચેના વિશેષો માટે પ્રથમ ક્રમના તત્વો સાથે પ્રથમ વર્તુળ પ્રક્રિયા વિશેષોમાં માન્ય રેક્ટિવ હોય છે, જેમાં સ્થિર તાપમાન છે.View Solution
$\mathrm{A}+\mathrm{B} \underset{\text { Step } 3}{\text { Step } 1} \mathrm{C} \xrightarrow{\text { Step } 2} \mathrm{P}$
પ્રથમના વર્તુળ પ્રક્રિયાની માહિતી નીચે સૂચવેલી છે.
સ્ટેપ Rate constant $\left(\sec ^{-1}\right)$
Activation energy
$\left(\mathrm{kJ} \mathrm{mol}^{-1}\right)$
$1$ ${k}_1$ $300$ $2$ ${k}_2$ $200$ $3$ ${k}_3$ $\mathrm{Ea}_3$ ઉપરોક્ત રીતેની પ્રક્રિયાનું વધારણીક વર્તુળ $(k)$ આપવામાં આવે છે. $\mathrm{k}=\frac{\mathrm{k}_1 \mathrm{k}_2}{\mathrm{k}_3}$ અને ઉપરોક્ત વધારણીક તાપ $(E_2)= 400$ કેલ્વિન છે, તો $\mathrm{Ea}_3$ નું મૂલ્ય છે $\mathrm{kJ} \mathrm{mol}^{-1}$ (નજીકની પૂર્ણાંક).
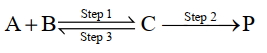
- 8પ્રક્રિયા $2N_2O_5\rightarrow 4NO_2 + O_2$ માટે નો દર અચળાંક $3.0 × 10^{-5 }s^{-1}$ છે. જો દર $2.40 × 10^{-5}$ મોલ $L^{-1} s^{-1}$ હોય,તો $N_2O_5$ ની સાંદ્રતા (મોલ $L^{-1}$) શોધો.View Solution
- 9$k =\left(6.5 \times 10^{12} \,s ^{-1}\right) e ^{-26000 K / T }$ને ધ્યાનમાં લો.જો આ પ્રક્રિયાસંયોજન $A$ના વિઘટન માટે અનુસરવામાં આવે છે.સક્રિયકરણ શક્તિ આ પ્રક્રિયા માટે $\dots\dots\dots\,\,kJ\,mol^{-1}$[નજીકના પૂર્ણાંકમાં] (આપેલ: $R =8.314 \,J\, K ^{-1}\, mol ^{-1}$ )View Solution
- 10ક્લોરિન પરમાણુઓની હાજરીમાં ઓઝોનની ઓકિસજન પરમાણુઓ સાથેની પ્રક્રિયા નીચે દર્શાવેલ બે તબક્કા મુજબ થઈ શકે છે.View Solution
${O_3}(g)\, + \,C{l^ * }(g)\, \to \,{O_2}(g) + Cl{O^ * }(g)$ ..... $(i)$ $[{K_i} = 5.2 \times {10^9}\,\,L\,mo{l^{ - 1}}\,{s^{ - 1}}]$
$Cl{O^ * }(g) + {O^ * }(g)\, \to \,{O_2}(g) + \,C{l^ * }(g)$ ..... $(ii)$ $[{K_{ii}} = 2.6 \times {10^{10}}\,\,L\,mo{l^{ - 1}}\,{s^{ - 1}}]$
તો સમગ્ર પ્રક્રિયા ${O_3}(g){\mkern 1mu} + {\mkern 1mu} {O^*}(g){\mkern 1mu} \to {\mkern 1mu} 2{O_2}(g)$ માટે સમગ્ર પ્રક્રિયાનો વેગ .......... $L\,\,mo{l^{ - 1}}\,{s^{ - 1}}$ અચળાંક કોની સૌથી નજીક હશે ?