An electric iron is connected to the mains power supply of $220V$. When the electric iron is adjusted at ‘minimum heating’ it consumes a power of $360W$ but at ‘maximum heating’ it takes a power of $840W$. Calculate the current and resistance in each case.
Given: $V = 220V, P_{min} = 360W, P_{max} = 840W$
For minimum heating case:
We know that
$P_{min} = VI$
$360 = 220XI$
$I = 1.63 amp$
$\text{R}=\frac{\text{V}}{\text{I}}$
$\text{R}=\frac{220}{1.63}$
$R = 134.96\ ohms$
For maximum heating case:
We know that
$P_{max} = VI$
$840 = 220XI$
$I = 3.81 amp$
$\text{R}=\frac{\text{V}}{\text{I}}$
$\text{R}=\frac{220}{3.81}$
$R = 57.74\ ohms$
For minimum heating case:
We know that
$P_{min} = VI$
$360 = 220XI$
$I = 1.63 amp$
$\text{R}=\frac{\text{V}}{\text{I}}$
$\text{R}=\frac{220}{1.63}$
$R = 134.96\ ohms$
For maximum heating case:
We know that
$P_{max} = VI$
$840 = 220XI$
$I = 3.81 amp$
$\text{R}=\frac{\text{V}}{\text{I}}$
$\text{R}=\frac{220}{3.81}$
$R = 57.74\ ohms$
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View SolutionIn 10s, a charge of 25C leaves a battery, and 200j of energy are delivered to an outside circuit as a result.
- What is the p.d. across the battery?
- What current flows from the battery?
- 2Two resistances when connected in parallel give resultant value of $2$ ohm; when connected in series the value becomes $9$ ohm. Calculate the value of each resistance.View Solution
- 3View SolutionAn electric heater is connected to the 230V mains supply. A current of 8A flows through the heater.
- How much charge flows around the circuit each second?
- How much energy is transferred to the heater each second?
- 4The electrical resistivities of four materials $A, B, C$ and $D$ are given below:View Solution
$\text{A}\ -110\times10^{-8}\Omega\text{ m}$
$\text{B}-\ 1.0\times10^{10}\Omega\text{ m}$
$\text{C}-\ 10.0\times10^{-8}\Omega\text{ m}$
$\text{D}-\ 2.3\times10^{3}\Omega\text{ m}$
Which material is:- Good conductor.
- Resistor.
- Insulator, and
- Semiconductor
- 5A flash of lightning carries $10\ C$ of charge which flows for $0.01\ s$. What is the current? If the voltage is $10MV$, what is the energy?View Solution
- 6When a current of $4.0A$ passes through a certain resistor for $10$ minutes,$ 2.88 \times 10J$ of heat are produced. Calculate:View Solution
- The power of the resistor.
- The voltage across the resistor.
- 7The electrical resistivities of three materials P, Q and R are given below:$\begin{matrix}\text{P}&2.3\times10^{3}\Omega\text{ m}\\\text{Q}&2.63\times10^{-8}\Omega\text{ m}\\\text{R}&1.0\times10^{15}\Omega\text{ m}\end{matrix}$View Solution
Which material will you use for making:- Electric wires.
- Handle for soldering iron, and
- Solar cells?
- 8View SolutionWhat would be the effect on the resistance of a metal wire of:
- Increasing its length?
- Increasing its diameter?
- Increasing its temperature?
- 9How will you connect three resistors of resistances $2Ω, 3Ω$ and $6Ω $ obtain a total n si stance of:View Solution
- $4 Ω,$
- $1Ω$
- 10For the circuit shown in the diagram below:View Solution
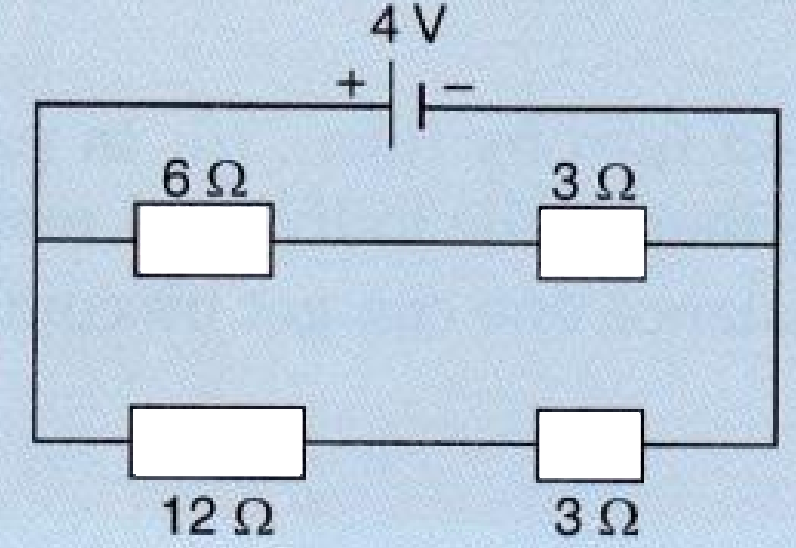
What is the value of :
Current through $6 Ω$ resistor?
Potential difference across $12 Ω$ resistor?
