Two resistances when connected in parallel give resultant value of $2$ ohm; when connected in series the value becomes $9$ ohm. Calculate the value of each resistance.
Two resistance when connected in series, resultant value is $9$ ohms.
Two resistance when connected in parallel, resultant values is $2$ ohms.
Let the two resistance be $R_1$ and $R_2$
If connected in series, then
$9 = R_1+ R_2$
$R_1 = 9 - R_2$
If connected in parallel, then
$\frac{1}{2}=\frac{1}{\text{R}_1}+\frac{1}{\text{R}_2}$
From aboves equations we get that
$\frac{1}{2}=\frac{(\text{R}_1+\text{R}_2)}{\text{R}_1\text{R}_2}$
$\frac{1}{2}=\frac{9}{(9-\text{R}_2)\text{R}_2}$
$9\text{R}_2-\text{R}_2{^2}=18$
$\text{R}_2{^2}-9\text{R}_2+18=0$
$(\text{R}_2-6)(\text{R}_2-3)=0$
$\text{R}_2=6,3$
So if $R_2$ $6$ ohms, then $R_1 = 9 - 6 = 3$ ohms.
If $R_2 = 3$ ohms, then $R_1 = 9 - 3 = 6$ ohms.
Two resistance when connected in parallel, resultant values is $2$ ohms.
Let the two resistance be $R_1$ and $R_2$
If connected in series, then
$9 = R_1+ R_2$
$R_1 = 9 - R_2$
If connected in parallel, then
$\frac{1}{2}=\frac{1}{\text{R}_1}+\frac{1}{\text{R}_2}$
From aboves equations we get that
$\frac{1}{2}=\frac{(\text{R}_1+\text{R}_2)}{\text{R}_1\text{R}_2}$
$\frac{1}{2}=\frac{9}{(9-\text{R}_2)\text{R}_2}$
$9\text{R}_2-\text{R}_2{^2}=18$
$\text{R}_2{^2}-9\text{R}_2+18=0$
$(\text{R}_2-6)(\text{R}_2-3)=0$
$\text{R}_2=6,3$
So if $R_2$ $6$ ohms, then $R_1 = 9 - 6 = 3$ ohms.
If $R_2 = 3$ ohms, then $R_1 = 9 - 3 = 6$ ohms.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1You are given one hundred $1 \Omega $ resister. What is the smallest and largest resistance you can make in a circuit using these?View Solution
- 2A $4 Ω$ coil and a $2 Ω$ coil are connected in parallel. What is their combined resistance? A total current of 3A passes through the coils. What current passes through the $2 Ω$ coil?View Solution
- 3The electrical resistivities of four materials P, Q, R and S are given below:View Solution
$\begin{matrix}\text{P}&6.84\times10^{-8}\Omega\text{m}\\\text{Q}&1.70\times10^{-8}\Omega\text{m}\\\text{R}&1.0\times10^{15}\Omega\text{m}\\\text{S}&11.0\times10^{-7}\Omega\text{m}\end{matrix}$
Which material will you use for making:- Heating element of electric iron.
- Connecting wires of electric iron.
- Covering of connecting wires?
- 4View SolutionDraw circuit symbols for:
- Fixed resistance.
- Variable resistance.
- A cell.
- A battery of three cells.
- An open switch.
- A closed switch.
- 5View SolutionState and explain Joule’s law of heating.
- 6View SolutionConsider the circuit given below where A, B and C are three identical light bulbs of constant resistance.
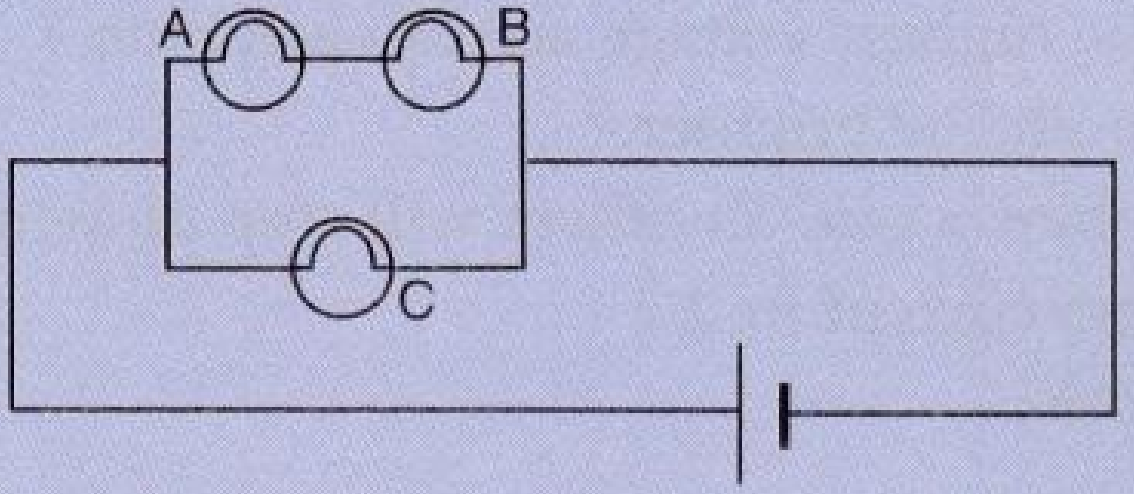
- List the bulbs in order of increasing brightness.
- If C burns out, what will be the brightness of A now compared with before?
- If B burns out instead, what will be the brightness of A and C compared with before?
- 7What is, highest, and lowest, resistance which can be obtained by combining Com resistors having the following resistances?View Solution
$4 Ω, 8 Ω, 12 Ω, 24 Ω$ - 8If the charge on an electron is $1.6 \times 10$ coulombs, how many electrons should pass through a conductor in $1$ second to constitute $1$ ampere current?View Solution
- 9The electrical resistivities of five substances A, B, C, D and E are given below:View Solution
$\begin{matrix}\text{B}&110\times10^{-8}\Omega\text{ m}\\\text{C}&2.60\times10^{-8}\Omega\text{ m}\\\text{D}&10.0\times10^{-8}\Omega\text{ m}\\\text{E}&1.70\times10^{-8}\Omega\text{ m}\end{matrix}$ - 10View SolutionHow does the resistance of a conductor depend on:
- Length of the conductor?
- Area of cross-section of the conductor?
- Temperature of the conductor?
