બે ધ્રુવક એકબીજાની નજીક છે. જ્યારે તેમાંથી એક $ 60^o$ કોણે પરિભ્રમણ કરે ત્યારે કેટલા......$\%$ ટકા અધ્રુવીભૂત પ્રકાશ તેમાંથી નિર્ગમન પામે?
Diffcult
b
અહીં બન્ને ધ્રુવક એકબીજાથી નજીક છે તેથી તે બન્ને વચ્ચેનો ધ્રુવીભવન દિશા કોણ \(90^o\) છે.
જ્યારે તેમાંથી એક \(60^o\) પરિભ્રમણ કરે, ત્યારે તે બન્ને વચ્ચેનો ધ્રુવીભવન દિશા કોણ \(30^o\) બને.
ધારો કે આપણે અધ્રુવીભૂત નિર્ગમન પામતા પ્રકાશની તીવ્રતા = \(I_0\)
અહીં બન્ને ધ્રુવક એકબીજાથી નજીક છે તેથી તે બન્ને વચ્ચેનો ધ્રુવીભવન દિશા કોણ \(90^o\) છે.
જ્યારે તેમાંથી એક \(60^o\) પરિભ્રમણ કરે, ત્યારે તે બન્ને વચ્ચેનો ધ્રુવીભવન દિશા કોણ \(30^o\) બને.
ધારો કે આપણે અધ્રુવીભૂત નિર્ગમન પામતા પ્રકાશની તીવ્રતા = \(I_0\)
તેથી પ્રથમ ધ્રુવક દ્વારા નિર્ગમ પામતા પ્રકાશ ની તીવ્રતા \({I_1} = \,\,\frac{1}{2}\,\,{I_0}\)
આ પ્રકાશ તલધ્રુવીભૂત છે અને તે દ્વિતીય ધ્રુવકમાંથી પસાર થશે.
દ્વિતીયક ધ્રુવકમાંથી નિર્ગમન પામતા પ્રકાશની તીવ્રતા\(I_2 = I_1\, cos^2\, \theta\)
\(\theta\) = બન્ને ધ્રુવક વચ્ચેનો કોણ
\({I_1} = \,\,\frac{1}{2}\,\,{I_0}\) અને \(\,\,\theta \,\, = \,\,3{0^ \circ }\) જેથી \({I_2} = \,\,{I_1}\,\,{\cos ^2}{30^ \circ }\, = \,\,\frac{1}{2}\,\,{I_0}\,\,{\cos ^2}{30^ \circ }\,\,\, \Rightarrow \,\,\,\frac{{{I_2}}}{{{I_0}}}\,\, = \,\,\frac{3}{8}\,\)
નિર્ગમન પ્રકાશ \( = \,\,\,\frac{{{I_2}}}{{{I_0}}}\,\, \times \,\,100\,\, = \,\,\frac{3}{8}\,\, \times \,\,100\,\,\, = \,\,37.5\,\%\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1વ્યતિકરણ ભાતમાં શલાકાની પહોળાઈ $\beta$ છે. જો સ્ત્રોતની આવૃત્તિ બમણી થાય તો શલાકાની પહોળાઈ .....View Solution
- 2View Solutionઉનાળાની ગરમ રાત્રે હવાનો વક્રીભવનાંક જમીનની નજીક લઘુતમ હશે અને જમીનથી ઉપર ઊંચાઇ સાથે વધતો જોય છે.હાઇગેનના સિદ્વાંત પરથી આપણે તારણ કાઢી શકીએ કે જયારે પ્રકાશ કિરણને સમક્ષિતિજ દિશામાં આપાત કરતાં,તે જયારે પ્રસરતું હોય ત્યારે કિરણપુંજ ________
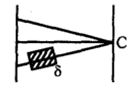
- 3આકૃતિમાં દ્વિ સ્લીટ પ્રયોગ બતાવ્યો છે. દરેક સ્લીટની પહોળાઈ $ W$ છે. એક જાડાઈનો, $\mu$ વક્રીભવનાંકવાળો પાતળો ગ્લાસનો ટુકડો સ્લીટ અને પડદાની વચ્ચે મુકવામાં આવે છે. કેન્દ્રીય બિંદુએ તીવ્રતા જાડાઈ ના વિધેય તરીકે માપવામાં આવે છે. જાડાઈ ની કઈ કિંમતે $C$ પર તીવ્રતા ન્યૂનત્તમ હશે?View Solution
- 4પ્રકાશીય ઉપકરણમાં વપરાતા પ્રકાશની તરંગલંબાઈ ${\lambda _1} = 4000 \mathring A$ અને ${\lambda _2} = 5000 \mathring A $ છે, તો તેમની વિભેદન શક્તિનો ગુણોત્તર (${\lambda _1}$ અને ${\lambda _2})$ ને અનુરૂપ) કેટલો મળે?View Solution
- 5View Solutionએક સ્લિટથી થતાં વિવર્તનમાં મધ્યસ્થ અધિકતમની નજીકની પ્રથમ ન્યુનતમ પર, સ્લિટની ધાર (એક છેડે) તથા તેના મધ્યમાં રહેલા બિંદુમાંથી ઉત્પન્ન થતી હાઇગેન્સ તરંગ અગ્રોની વચ્ચેનો કળા તફાવત કેટલો હશે?
- 6View Solutionવ્યતિકરણ પ્રયોગમાં મહત્તમ અને ન્યૂનત્તમ વચ્ચેનું અંતર .......
- 7યંગ પ્રયોગમાં $interfering\,beam$ માંથી કોઇ એકમાં $7\,micron$ ની જાડાઈની શીટ અને $\mu=1.6$ ની શીટ મૂકવામાં આવે, તો મધ્યની શલાકા એ $7\,m$ પ્રકાશિત શલાકાની જગ્યા લે છે. વપરાયેલા પ્રકાશની તરંગલંબાઈ $............\mathring A$View Solution
- 8સિંગલ સ્લીટના પ્રયોગમાં વિવર્તન ભાતમાં લાલ રંગ માટેનું પ્રથમ ન્યૂનતમ બીજી તરંગલંબાઈના પ્રથમ મહત્તમ સાથે સંપાત થાય છે. જો લાલ રંગની તરંગલંબાઈ $6600\,\mathop A\limits^o$ હોય તો પ્રથમ મહત્તમની તરંગલંબાઈ ($\mathop A\limits^o $ માં) કેટલી હશે?View Solution
- 9બે સ્લિટનો પ્રયોગ $ 500\, nm$ તરંગલંબાઈ ધરાવતા પ્રકાશ સાથે કરવામાં આવે છે. જો પાતળી તકતીની જાડાઈ $ 2\, \mu m $ અને વક્રીભવનાંક $1.5 $ હોય અને તેને સ્લીટની આગળ મૂકવામાં આવે, તો કેન્દ્રીય શલાકાનું સ્થાન .......View Solution
- 10View Solutionવ્યતિકરણમાં બે ઉદગમ કેવા હોવા જોઈએ.
