બે તરંગો $ y_1 = a sin(\omega t) $ અને $ {y_2} = b\cos (\omega t) $ વચ્ચે કળા તફાવત કેટલો થાય?
Easy
Download our app for free and get started
b
(b)\({y_1} = a\sin \omega t,\)and \({y_2} = b\cos \omega t = b\sin \left( {\omega \,t + \frac{\pi }{2}} \right)\) So phase difference \(\phi = \pi /2\)
(b)\({y_1} = a\sin \omega t,\)and \({y_2} = b\cos \omega t = b\sin \left( {\omega \,t + \frac{\pi }{2}} \right)\) So phase difference \(\phi = \pi /2\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionનીચેનામાંથી કઈ ઘટના હાઈગેનનો સિદ્ધાંત સમજાવી શકતી નથી?
- 2View Solutionટેલિસ્કોપના વસ્તુ કાચના લેન્સનો અપર્ચર મોટો રાખવામા આવે છે કે જેથી
- 3View Solutionયંગના બે સ્લિટનાં પ્રયોગમાં, એક સ્લિટની પહોળાઈ બીજી સ્લિટની પહોળાઈ કરતાં ત્રણ ગણી છે. સ્લિટમાંથી બહાર આવતા પ્રકાશનો કંપવિસ્તાર સ્લિટ-પહોળાઈનાં સમપ્રમાણમાં હોય છે. વ્યતિકરણભાતમાં મહત્તમ અને ન્યૂનતમ તીવ્રતાઓનો ગુણોત્તર ........... થશે.
- 4View Solutionવ્યતિકરણની ઘટના ..... થી દેખાય છે.
- 5પ્રકાશીય ઉપકરણમાં વપરાતા પ્રકાશની તરંગલંબાઈ ${\lambda _1} = 4000 \mathring A$ અને ${\lambda _2} = 5000 \mathring A $ છે, તો તેમની વિભેદન શક્તિનો ગુણોત્તર (${\lambda _1}$ અને ${\lambda _2})$ ને અનુરૂપ) કેટલો મળે?View Solution
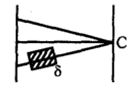
- 6આકૃતિમાં દ્વિ સ્લીટ પ્રયોગ બતાવ્યો છે. દરેક સ્લીટની પહોળાઈ $ W$ છે. એક જાડાઈનો, $\mu$ વક્રીભવનાંકવાળો પાતળો ગ્લાસનો ટુકડો સ્લીટ અને પડદાની વચ્ચે મુકવામાં આવે છે. કેન્દ્રીય બિંદુએ તીવ્રતા જાડાઈ ના વિધેય તરીકે માપવામાં આવે છે. જાડાઈ ની કઈ કિંમતે $C$ પર તીવ્રતા ન્યૂનત્તમ હશે?View Solution
- 7યંગના પ્રયોગમા $5$મુ મહતમ અને $3$ જી લઘુતમ વચ્ચેનુ અંતર શલાકાની પહોળાઈ કરતા કેટલુ ગણુ હશે ?View Solution
- 8$4I$ અને $9I$ તીવ્રતા ધરાવતા બે પ્રકાશ, પડદા ઉપર વ્યતિકરણ અનુભવે છે. પડદા ઉપર $A$ બિંદુ આગળ કળા તફાવત શૂન્ય. અને બિંદુ $B$ આગળ $\pi$ છે. બિંદુ $A$ અને $B$ આગળ પરિણામી તીવ્રતાઓનો તફાવત $........\,I$ થશે.View Solution
- 9View Solutionપ્રકાશના તરંગો લંબગત તરંગો છે,કારણ કે
- 10$I_1 $ અને $I_2$ તીવ્રતા ધરાવા બે તરંગો એક જ દિશામાં કોઇ એક વિસ્તારમાં સમાન સમયે પસાર થઇ રહ્યા છે. મહત્તમ અને લઘુત્તમ તીવ્રતાનો સરવાળો કેટલો થાય?View Solution