$\frac{1}{3 \sqrt{3}}$ જેટલા ઘર્ષણાંક ધરાવતી સમક્ષિતીજ ખરબચડી સપાટી પર $3\, kg$ દળ ધરાવતાં ચોસલાને આકૃતિમાં દર્શાવ્યા મુજબ ગોઠવવામાં આવ્યો છે. દર્શાવ્યા અનુસાર સમક્ષિતીજ સાથે $60°$ કોણ રચતા ઉર્ધ્વ સપાટી પર જરૂરી બળનું ઓછામાં ઓછું મૂલ્ય $3x$ છે કે જેથી તે ચોસલું ખસી ના શકે. $3x$ નું મૂલ્ય ......... હશે.
$\left[g=10 m / s ^{2} ; \sin 60^{\circ}=\frac{\sqrt{3}}{2} ; \cos 60^{\circ}=\frac{1}{2}\right]$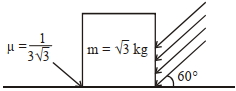
JEE MAIN 2021, Diffcult
Download our app for free and get started
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$10 \,kg$ દળનાં એક બ્લોકને $30^{\circ}$ નો ઢોળાવ ખૂણો ધરાવતી નિશ્વિત ખરબચડી $(\mu=0.8)$ કોણીય સપાટી પર મુકેલ છે. બ્લોક પર લાગતું ઘર્ષણબળ ............ $N$ છે.View Solution
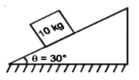
- 2જો સમાન દળના બે કણની વક્રતા ત્રિજ્યાઓનો ગુણોત્તર $3:4$ હોય, તો તેમના કેન્દ્રગામી પ્રવેગ અચળ રહે તે માટે તેમના વેગનો ગુણોત્તર._________હોય.View Solution
- 3View Solutionમહત્તમ સ્થિર ઘર્ષણ બળ
- 4આપેલ આકૃતિમાં, એક $m$ દળનો ગોળો બે સમાન લંબાઈની દોરીઓ વડે જોડેલ છે. જો સળીયાના કોણીય વેગ $\omega$ સાથે ફેરવામાં આવે છે, તો પછીView Solution
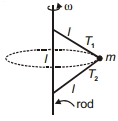
- 5View Solutionજ્યારે પદાર્થ સપાટી પર ગતિ કરતો તો તે ઘર્ષણબળ ને ....
- 6$2 \,kg $ ના દળનો બ્લોક $0.4$ ઘર્ષણાંક ઘરાવતી સપાટી પર પડેલ છે.જો તેના પર $2.5\, N$ નું બળ લગાવતાં ઘર્ષણબળ ........ $N$ થાય.View Solution
- 7View Solutionએક હોકી નો ખેલાડી ઉત્તર તરફ ગતિ કરે છે અને પ્રતિસ્પર્ધીથી દૂર રહેવા અચાનક પશ્ચિમ તરફ સમાન ઝડપે વળાંક લે છે. ખેલાડી પર લાગેલું બળ કેવું હશે?
- 8$m_1=5 $ $kg$ અને $m_2=10$ $kg$ બે દળોને ઘર્ષણરહિત ગરગડી ઉપર ખેંચી ન શકાય તેવી દોરીથી બાંધી,આકૃતિમાં દર્શાવ્યા અનુસાર ગતિ કરે છે.સમક્ષિતિજ સપાટી માટે ઘર્ષણાંકનું મૂલ્ય $0.15$ છે.આ ગતિને રોકવા માટે $m_2$ ઉપર તરફ મૂકવું લઘુત્તમ દળ $m$ ........ $kg$ થશે.View Solution
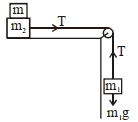
- 9એક મુસાફર-બેગેને $2 \,m / s$ ની ઝડપથી ગતિ કરતા કન્વેયર-બેલ્ટ પર હળવેકથી છોડવામાં આવે છે. કન્વેયર-બેલ્ટ અને બેગ વચ્ચે ધર્ષણાંક $0.4$ છે. પ્રારંભમાં આ બેગ કન્વેયર બેલ્ટ ઉપર સરકે છે, પરંતુ ત્યારબાદ ઘર્ષણને કારણો સ્થિર થઈ જાય છે. મુસાફર-બેગની બેલ્ટ ઉપર તેની સરકવાની સ્થિતિમાં કપાયેલ અંતર ........... $m$ હશે. [g $=10 \,m / s ^{-2}$ લો.]View Solution
- 10એક ટેબલ તેના કેન્દ્રમાંથી પસાર થતી શિરોલંબ અક્ષની આસપાસ $20\ rad/s$ ના કોણીય વેગથી ભ્રમણ કરે છે તેની પોતાની ઉપર એક ફલાય વ્હીલ જોડેલું છે જેની સમક્ષિતિજ ધરી સાથે બેરિંગ જોડેલી છે તેની આસપાસ $40\ rad/s$ થી ભ્રમણ કરે છે. વ્હીલનો પરિણામી કોણીય વેગ..... હશે.View Solution