દ્વિતીય ક્રમ પ્રક્રિયા માટે કે જેના બંને પ્રક્રિયકો સમાન પ્રારંભિક સાંદ્રતા ધરાવે છે અને પ્રક્રિયા $20\%$ પુરી થવા માટે $500$ સેકન્ડ લાગે છે. તો પ્રક્રિયાને $80\%$ પુરી થવા ......... સેકન્ડ લાગશે.
Diffcult
Download our app for free and get started
b
\(\,K\,\, = \,\,\frac{1}{t}\,\, \times \,\frac{a}{{a(a\, - \,\,x)}}\)
\(\,K\,\, = \,\,\frac{1}{t}\,\, \times \,\frac{a}{{a(a\, - \,\,x)}}\)
\(20\% \,\) સંપૂર્ણ થવા માટે \(\,{\text{K}}\, = \,\,\frac{{\text{1}}}{{{\text{500}}}}\,\, \times \,\,\frac{{20}}{{100\,\, \times \,\,80}}\,\,\,\,\,\,..........(1)\)
\(80\% \) પૂર્ણ થવા માટે \({\text{K}}\,\, = \,\,\frac{{\text{1}}}{{\text{t}}}\,\, \times \,\,\frac{{80}}{{100\,\, \times \,\,20}}\,\,\,\,\,\,............(2)\)
\(\frac{1}{{500}}\,\, \times \,\,\frac{{20}}{{100\,\, \times \,\,80}}\,\, = \,\,\frac{1}{t}\,\, \times \,\,\frac{{80}}{{100\,\, \times \,\,20}}\)
\(t\,\, = \,\,3000\,\,\sec .\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionકેમિકલ સ્પીસિસ કેવી રીતે પ્રક્રિયા આપે છે તે સમજાવવા માટે કોલીસન થિયરીનો ઉપયોગ થાય છે. આ સિદ્ધાંત અને ગતિકીય પરમાણુ નમૂનો રાસાયણિક પ્રક્રિયાના દરે નીચેનામાંથી કયા અસર કરતાં નથી ?
- 2લાકડા ના એક ટૂકડામાં $\frac{{ }^{14} \mathrm{C}}{{ }^{12} \mathrm{C}}$ નો ગુણોત્તર, વાતાવરણ ની તુલના માં $\frac{1}{8}$ મો ભાગ છે. જો ${ }^{14} \mathrm{C}$ નો અર્ધ આયુષ્ય $5730$ વર્ષ હોય તો, લાકડાના નમૂનાની ઉંમર (આયુ)___________ છે.View Solution
- 3શૂન્ય ક્રમ પ્રક્રિયા માટે $K= 2 \times 10^{-2}$ મોલ $L^{-1}$ સેકન્ડ $^{-1}$ છે. જો $25$ સેકન્ડ પછી પ્રક્રિયકની સાંદ્રતા $0.5\,M$ થાય તો તેની પ્રારંભિક સાંદ્રતા ...... $M$ હોવી જોઈએ.View Solution
- 4પ્રથમ ક્રમની પ્રક્રિયા માટે,$90\%$ પ્રક્રિયા પૂર્ણ થવા માટે લાગતો સમય, પ્રક્રિયાના અર્ધ આયુષ્ય કરતા ' $x$ ' ગણો છે. તો ' $x$ નું મૂલ્ય શોધો. (આપેલ: $\ln 10=2.303$ અને $\log 2=0.3010$ )View Solution
- 5શૂન્ય ક્રમની પ્રક્રિયા માટે $K$ નો એકમ દર્શાવો.View Solution
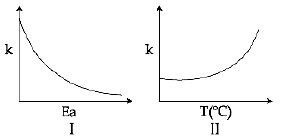
- 6આર્હેનિયસના સમીકરણને અનુસરતિ કોઈ એક પ્રક્રિયાના આલેખો નીચે આપેલા છે $(0\,^oC < T < 300\,^oC)$ ($k$ અને $E_a$ અનુક્રમે પ્રક્રિયા વેગ અને સક્રીયકરણ ઉર્જા છે ) તો નીચેનામાથી શું થશે?View Solution
- 7પ્રક્રિયા :View Solution
$2N_2O_5 \rightarrow 4NO_2 + O_2$ નો દર ત્રણ રીતે લખી શકાય.
$\frac{-d[N_2O_5 ]}{dt} = k[N_2O_5]$
$\frac{d[NO_2 ]}{dt} = k'[N_2O_5]\,;$ $\frac{d[O_2 ]}{dt} = k"[N_2O_5]$
$k$ અને $k'$ તથા $k$ અને $k''$ વચ્ચેનો સંબંધ .............
- 8ક્લોરિન પરમાણુઓની હાજરીમાં ઓઝોનની ઓકિસજન પરમાણુઓ સાથેની પ્રક્રિયા નીચે દર્શાવેલ બે તબક્કા મુજબ થઈ શકે છે.View Solution
${O_3}(g)\, + \,C{l^ * }(g)\, \to \,{O_2}(g) + Cl{O^ * }(g)$ ..... $(i)$ $[{K_i} = 5.2 \times {10^9}\,\,L\,mo{l^{ - 1}}\,{s^{ - 1}}]$
$Cl{O^ * }(g) + {O^ * }(g)\, \to \,{O_2}(g) + \,C{l^ * }(g)$ ..... $(ii)$ $[{K_{ii}} = 2.6 \times {10^{10}}\,\,L\,mo{l^{ - 1}}\,{s^{ - 1}}]$
તો સમગ્ર પ્રક્રિયા ${O_3}(g){\mkern 1mu} + {\mkern 1mu} {O^*}(g){\mkern 1mu} \to {\mkern 1mu} 2{O_2}(g)$ માટે સમગ્ર પ્રક્રિયાનો વેગ .......... $L\,\,mo{l^{ - 1}}\,{s^{ - 1}}$ અચળાંક કોની સૌથી નજીક હશે ?
- 9$2N_2O_5 \rightarrow 4NO_2 + O_2$ પ્રક્રિયા માટે જો $NO_2$ ની સાંદ્રતા $1.6 × 10^{-2}$ સેકન્ડમાં વધે છે તો $ NO_2$ નો નિર્માણ દર.....View Solution
- 10$A$ $\rightarrow$ $ B$ આઈસોમરાઈઝેશન પ્રથમ પ્રક્રિયા માટેનો દર અચળાંક $ 4.5 \times 10^{-3}$ છે. જો $A$ ની પ્રારંભિક સાંદ્રતા $1\,M$ હોય, તો $1$ કલાક પછી પ્રક્રિયાનો દર શોધો?View Solution