એક $10 \;H$ નું આદર્શ ગુંચળું અવરોધ $5 \;\Omega$ અને $5 \;V$ ની બેટરી સાથે શ્રેણીમાં જોડેલ છે. જોડાણ કર્યાની $2$ સેકન્ડ પછી ગૂંચળામાં કેટલા અમ્પિયરનો વિદ્યુતપ્રવાહ વહેશે?
AIEEE 2007, Medium
Download our app for free and get started
b
\(I=I_{o}\left(1-e^{-\frac{R}{L} t}\right)\)
\(I=I_{o}\left(1-e^{-\frac{R}{L} t}\right)\)
(When current is in growth in \(L R\) circuit)
\(=\frac{E}{R}\left(1-e^{-\frac{R}{L} t}\right)=\frac{5}{5}\left(1-\mathrm{e}^{-\frac{5}{10} \times 2}\right)=\left(1-e^{-1}\right)\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionજ્યારે સોલેનોઈડના ગુચળાના આડછેડનું ક્ષેત્રફળ અચળ રાખીને તેમાં આંટાની સંખ્યા અને લંબાઈ બમણી કરવામાં આવે તો તેનો ઇન્ડક્ટન્સ .....
- 2એક આદર્શ ટ્રાન્સફોર્મરના પ્રાથમિકમાં $100$ આંટાઓ અને ગૌણમાં $250$ આંટાઓ છે એસી વિદ્યુતસ્થિતિમાનનું મહત્તમ મૂલ્ય $28\; V$ છે તો $r.m.s.$ મૂલ્ય આશરે કેલલંં છે?View Solution
- 3ઈન્ડક્ટરને સ્વીચથી $DC$ વૉલ્ટેજ સપ્લાય સાથે જોડતા હવે,View Solution
- 4View Solutionધાતુની રીંગની નજીક ઉતરધ્રુવ લાવતા તેમાં ઉત્પન્ન થતો પ્રવાહ કેટલો હશે ?
- 5$1\,H$ પ્રેરણ અને $100\,\Omega$ નો અવરોધ ધરાવતા ગૂંચળા (ગાળા) ને $6\,V$ ની બેટરી સાથે જોડવામાં આવેલ છે.View Solution
$(a)$ સ્થિત-સ્થિતિના મૂલ્યના પ્રવાહ કરતાં અડધો પ્રવાહ થાય તે માટે લાગતો સમય અને
$(b)$ પરિપથમાં કળ ચાલુ કર્યા બાદ $15 \;ms$ સમયે ગૂંચળા સાથે સંકળાયેલ ચુંબકીયક્ષેત્રમાં સંગ્રહિત ઊર્જા શોધો. $\left(\ln 2=0.693, e ^{-3 / 2}=0.25\right.$ આપેલ છે.)
- 6$20$ આંટા અને $25\, cm^2$ લંબચોરસ કોઇલનો અવરોધ $100\;\Omega$ છે. જો કોઈલના સમતલને લંબ રહેલું ચુંબકીયક્ષેત્ર $1000 \,Tesla/sec$ ના દરથી બદલાય છે, તો કોઇલમાં કેટલો પ્રવાહ ($ampere$ માં) ઉત્પન્ન થાય?View Solution
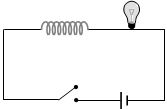
- 7View Solutionઆપેલ પરિપથમાં બલ્બ અચાનક પ્રકાશિત થશે જો ....
- 8વિધાન $- 1$ : $L$ લંબાઈ, $N$ આંટા અને $r$ ત્રિજ્યા ધરાવતા લાંબા સોલેનોઇડનું આત્મપ્રેરકત્વ $\frac{{\pi {\mu _0}{N^2}{r^2}}}{L}$ કરતાં ઓછું હોય.View Solution
વિધાન $- 2$ : વિધાન $- 1$ માં આપેલ સોલેનોઇડમાંથી $I$ પ્રવાહ વહેતો હોય તો સોલેનોઇડની વચ્ચે ચુંબકીય પ્રેરણ $\frac{{{\mu _0}NI}}{L}$ જેટલું મળે છે જે છેડા તરફ જતાં ઘટતું જાય છે.
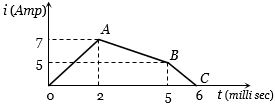
- 9$4.6\, H$ ઇન્ડકટરમાંથી પસાર થતા પ્રવાહનો આલેખ આપેલ છે,તો $t = 5 \,lmilli-sec$ થી $6 \,milli-sec$માં કેટલો $emf$ ઉત્પન્ન થાય?View Solution
- 10$20 \,cm$ લંબાઈના એક ધાત્વીય સળિયાને ઉત્તર-દક્ષિણ દિશામાં મૂકવામાં આવેલ છે અને તેને $20 \,m / s$ ની અચળ ઝડપે પૂર્વ દિશામાં ગતિ કરાવવામાં આવે છે. આ સ્થાને પૃથ્વીના ચુંબકીય ક્ષેત્રનો સમક્ષિતિજ ધટક $4 \times 10^{-3} \,T$ અને ડીપ-કોણ $45^{\circ}$ છે. સળિયામાં પ્રેરિત $emf$ ............$mV$ થશે.View Solution