एक आयताकार कुण्डली का क्षेत्रफल 25 सेमी $^2$, प्रतिरोध $100 \Omega$ तथा फेरों की संख्या 20 है। यदि चुम्बकीय क्षेत्र कागज के तल के लम्बवत् हो तथा 1000 टेसला/सेकण्ड की दर से बदलता हो तो धारा का मान है
[1992]
Download our app for free and get started
(c) $i =\frac{ e }{ R }$
$ =\frac{ n }{ R } \frac{ AdB }{ dt }=\frac{20 \times 25 \times 10^{-4} \times 1000}{100}=0.5 A $
$ =\frac{ n }{ R } \frac{ AdB }{ dt }=\frac{20 \times 25 \times 10^{-4} \times 1000}{100}=0.5 A $
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionएक चालक लूप में बनने वाला आवेश, जबकि वह चुम्बकीय क्षेत्र में हो, निर्भर करेगा
- 2एक परिपथ जिसका प्रतिरोध $R$ है उसमें लगने वाला चुम्बकीय फ्लक्स $\Delta \phi, \Delta t$ समय में बदल जाता है तो परिपथ में बनने वाला कुल आवेश $Q , \Delta t$ समय में है:View Solution
- 3एक कुण्डली का स्वप्रेरण गुणांक होगा, जिसमें $5 V$ का वि.बा.व. बनता हो जबकि धारा $3 A$ से $2 A , 1$ मिली सेकण्ड में परिवर्तित होती होView Solution
- 4किसी लम्बी परिनालिका में फेरों की संख्या $1000$ है। जब परिनालिका से $4 A$ धारा प्रवाहित होती है, तब इस परिनालिका के प्रत्येक फेरे से संबद्ध चुम्बकीय फ्लक्स $4 \times 10^{-3} Wb$ है । इस परिनालिका का स्व$-$प्रेरकत्व है:View Solution
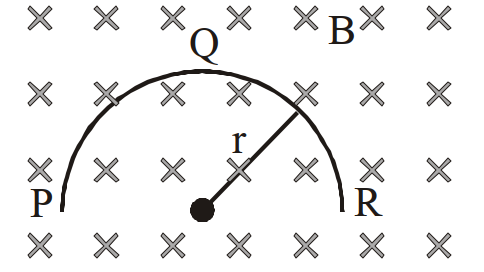
- 5$r$ त्रिज्या की एक पतली अर्द्धवृत्ताकार चालक रिंग (वलय) $( PQR )$ किसी क्षैतिज चुम्बकीय क्षेत्र $B$ में गिर रही है। गिरते समय इसका समतल, आरेख में दर्शाये गये अनुसार, ऊध्र्वाधर रहता है। जब गिरती हुई रिंग की चाल $v$ है तो, इसके दो सिरों के बीच विकसित विभवान्तर होगाView Solution
- 6View Solutionएक प्रेरक (inductor) में ऊर्जा संचित होती है-
- 7एक आयताकार, एक वर्गाकार, एक वृत्तीय और एक दीर्घवृत्तीय फन्द जो सभी $x - y$ तल में हैं, एक अचर चुम्बकीय क्षेत्र से स्थिर वेग $\overrightarrow{ V }= v \hat{ i }$ से बाहर निकल रहे हैं। चुम्बकीय क्षेत्र की दिशा ऋणात्मक $z$ अक्ष की दिशा में है। क्षेत्र से बाहर निकलने के प्रक्रम में इन फन्दों में प्रेरित वि.वा.ब (emf) स्थिरमानी नहीं रहेगा :-View Solution
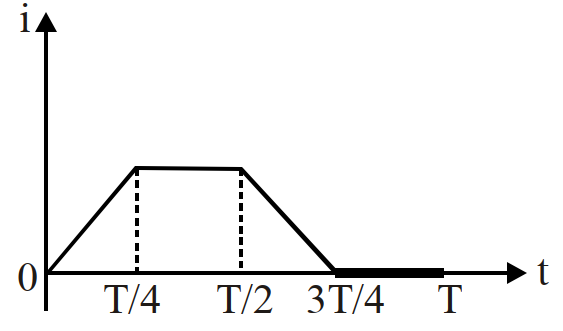
- 8किसी कुण्डली में विद्युतधारा $i$ का मान आरेखानुसार समय के साथ परिवर्तित होता है, तो प्रेरित विद्युत वाहक बल का मान समय के साथ परिवर्तित होगा:View Solution
- 9एक चालक वृताकार पाश ( लूप) को किसी एकसमान चुम्बकीय क्षेत्र में रखा गया है। चुम्बकीय क्षेत्र की तीव्रता $B=.025 T$ है और इसका तल पाश के लम्बवत् है। पाश की त्रिज्या को $1 mm s ^{-1}$ की स्थिर दर से सिकुड़ने दिया जाता है। पाश की त्रिज्या 2 सेमी होने पर उसमें प्रेरिज विद्युत वाहक बल (e.m.f.) हैView Solution
- 10एक $0.4$ मी लम्बाई वाला चालक $7$ मी/सेकण्ड से चुम्बकीय क्षेत्र $B =0.9$ वेबर $/$ मी $^2$ के लम्बवत् घूमता है। इसमें प्रेरक वि.वा.ब. होगा :View Solution