નજીક બિંદુના ઓછામાં ઓછા અંતર \(25\,\, cm\) માટે, મેગ્નિફાઇગ પાવર
આ સ્થિતિમાં ટેલિસ્કોપ ના મેગ્નિફાઈગ પગાર \(MP\,\,\)
\( = \,\,\, - \frac{{{{{f}}_0}}}{{{{{f}}_e}}}\,\,\left( {1 + \frac{{{{{f}}_e}}}{D}} \right)\,\, = \,\,\, - \frac{{60}}{5}\,\,\,\left( {1 + \frac{5}{{25}}} \right)\,\, = \,\,\, - \frac{{12\,\, \times \,\,6}}{5}\,\, = \,\,\, - 14.4\)
હવે,\(\frac{1}{{{{{f}}_e}}}\,\, = \,\,\frac{1}{{{v_e}}}\,\, - \,\,\frac{1}{{{u_e}}}\,\,\, \Rightarrow \,\,\frac{1}{5}\,\, = \,\, - \frac{1}{{25}}\,\, - \,\frac{1}{{{u_e}}}\,\,\, \Rightarrow \,\,\,\frac{{ - 1}}{{{u_e}}}\,\, = \,\,\frac{1}{{25}}\,\, + \,\,\frac{1}{5}\)
\( \Rightarrow \,\,{u_e} = \,\, - 4.17\,\,cm\,\,\,\,\,\,\, \Rightarrow \,\,\,|{u_e}|\,\, = \,\,4.17\,\,cm\)
આ સ્થિતિમાં ટેલિસ્કોપની લંબાઇ \(L\,\, = \,\,\,{{{f}}_0} + |{u_e}|\,\, = \,\,60\,\, + \,\,4.17\,\, = \,\,64.17\,\,cm\)
Download our appand get started for free
Similar Questions
- 1View Solutionએક બહિર્ગોળ લેન્સમાં પહેલાં વાદળી રંગના પ્રકાશનો ઉપયોગ કરવામાં આવે છે. ત્યારબાદ વાદળીના બદલે રાતા રંગના પ્રકાશનો ઉપયોગ કરવામાં આવે તો તેની કેન્દ્રલંબાઈ ......
- 2$\frac{5}{3}$ વક્રીભવનાંક ધરાવતા પાણીની સપાટીથી $4 \,m$ ઊંડાઈએ એક બિંદુવત પ્રકાશ ઉદ્ગમ છે. પાણીની મુકત સપાટી પરથી બહાર આવતો પ્રકાશ અટકાવવા માટે ઉદ્ગમસ્થાનની બરાબર ઉપર, પાણીની સપાટી પર કેટલા વ્યાસવાળી ($m$ માં) અપારદર્શક તકતી મૂકવી જોઇએ?View Solution
- 3$100\,W$ તથા $5\,\%$ પાવર ધરાવતા બલ્બ એ જોઈ શકાય તેવું વિકીરણ પેદા કરે છે.તો $10\,m$ ના અંતરે સરેરાશ જોઈ શકાય તેવા વિકીરણની તીવ્રતાView Solution
- 4પ્રિઝમનો લઘુત્તમ વિચલનકોણ $ 30^o $ અને પ્રિઝમકોણ $60^o $ હોય,તો પ્રિઝમનો વક્રીભવનાંક કેટલો હશે?View Solution
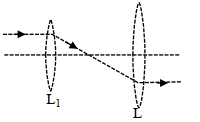
- 5નીચેની આકૃત્તિ અનુક્રમે $10 \mathrm{~cm}$ અને $15 \mathrm{~cm}$ કેન્દ્રલંબાઈ ધરાવતા બે દ્વિ-બહિર્ગોળ લેન્સ $L_1$ અને $L_2$ દર્શાવે છે. $L_1$ અને $L_2$ વચ્ચેનું અંતર ........ થશે.View Solution
- 6બંને સપાટીની વક્રતાત્રિજ્યા $R$ ધરાવતા બહિગોળ લેન્સનો પાવર $p$ છે તો સમાન દ્રવ્યમાંથી બનાવેલ સમતલ બહિગોળ લેન્સ નો પાવર $1.5P$ હોય તો તેની વક્રતાત્રિજ્યા ........$R$View Solution
- 7દૂરની દ્રષ્ટિ માટે ન્યૂનત્તમ અંતર $25\,\, cm$ છે. $5\,\, cm$ કેન્દ્રલંબાઈના સાદા સૂક્ષ્મદર્શક યંત્રનો પાવર શોધો જો અંતિમ પ્રતિબિંબ દૂરની દ્રષ્ટિથી ન્યૂનત્તમ અંતરે મળતું હોય?View Solution
- 8$R$ ત્રિજયાની ગોળીય સ્કીનના કેન્દ્ર પર નાનો સમતલ અરીસો મૂકેલ છે. પ્રકાશના કિરણો અરીસા પર આપાત કરવામાં આવે છે.અરીસાને દર સેકન્ડે $n$ પરિભ્રમણ કરાવવાથી તેના દ્વારા પરાવર્તન પામતા પ્રકાશની સ્કીન પર ઝડપ કેટલી થશે?View Solution
- 9એક કાંચનો વક્રીભવનાંક $1.5$ છે, શૂન્યાવકાશમાંથી પસાર થતાં પ્રકાશના કિરણની તંગલંબાઇ $6000\;\mathring A$ છે જે આ કાંચમાંથી પસાર થાય ત્યારે તેની તરંગલંબાઈ કેટલા $\mathring A$ હશે?View Solution
- 10View Solutionપાછળની બાજુએ જોવાના અરીસા માટે દિવસ અને રાતની ગોઠવણીઓ શેનો ઉપયોગ કરે છે ?
