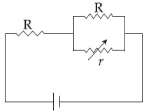
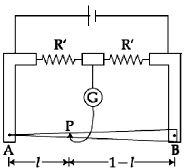
એક મીટરબ્રીજમાં, $1\,m$ લંબાઈનો તાર અસમાન આડછેદ એવી રીતે ધરાવે છે કે તેના અવરોધ $R$ નો લંબાઈ $l$ સાથેનો ફેરફાર $\frac{{dR}}{{d\ell }} \propto \frac{1}{{\sqrt \ell }}$ છે. આકૃતિમાં બતાવ્યા પ્રમાણે બે સમાન અવરોધો જોડેલ છે. જ્યારે જોકી એ બિંદુ $P$ પર હોય ત્યારે ગેલ્વેનોમીટરમાં આવર્તન શૂન્ય છે. લંબાઈ $AP$ કેટલા .................. $m$ હશે?

JEE MAIN 2019, Diffcult
c
\(\frac{\mathrm{d} \mathrm{R}}{\mathrm{d} \ell}=\frac{\mathrm{k}}{\sqrt{\ell}} \quad \mathrm{k}=\mathrm{constant}\)
\(\frac{\mathrm{d} \mathrm{R}}{\mathrm{d} \ell}=\frac{\mathrm{k}}{\sqrt{\ell}} \quad \mathrm{k}=\mathrm{constant}\)
\(\int_{0}^{R} d R=k \int_{0}^{1} \frac{d \ell}{\sqrt{\ell}}\)
\(\mathrm{R}=2 \mathrm{k}\) resistance of wire \(\mathrm{AB}\)
Again, \(\int_{0}^{R / 2} \mathrm{d} \mathrm{R}=\mathrm{k} \int_{0}^{L} \frac{\mathrm{d} \ell}{\sqrt{\ell}} \quad \mathrm{L} \rightarrow\) Length \(\mathrm{AP}\)
\(\frac{\mathrm{R}}{2}=\mathrm{k} 2 \mathrm{L}^{1 / 2} \quad ; \quad \mathrm{k}=\mathrm{k} 2 \mathrm{L}^{1 / 2}\)
\(\Rightarrow \quad \mathrm{L}=\frac{1}{4} \,\mathrm{m}=0.25\, \mathrm{m}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionહીટર કોઇલને બે સરખા ભાગમાં વિભાજીત કરીને એક ટુકડાને હીટર સાથે લગાવવામાં આવે છે.અડઘી કોઇલથી ઉત્પન્ન થતી ઉષ્મા અને આખી કોઇલ દ્રારા ઉત્પન્ન થતી ઉષ્માનો ગુણોતર કેટલો થાય?
- 2$3 × 10^{–7}\,\Omega-m $ અવરોધકતા અને $1\, cm× 1\, cm ×100\, cm $ પરિમાણ ધરાવતા બ્લોકનો લંબચોરસ બાજુ વચ્ચેનો અવરોધ કેટલો થાય?View Solution
- 3$2\,Ω$ અવરોધમાંથી કેટલા ........ $A$ પ્રવાહ પસાર થાય?View Solution
- 4બે વાહક તારોને શ્રેણીમાં જોડતાં સમતુલ્ય અવરોધ $14\, \Omega$ અને તેમને સમાંતરમાં જોડતાં સમતુલ્ય અવરોધ $3.43\, \Omega$ થાય છે. તો તે પૈકી વધુ મૂલ્ય ધરાવતાં તારનો અવરોધ ................. $\Omega$View Solution
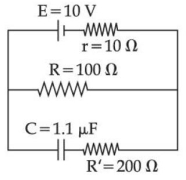
- 5આકૃતિમાં દર્શાવેલ પરીપથમાં સ્થિત સ્થિતિમાં સંઘારકમાં સંગ્રહિત વિદ્યુતભાર $.......\times 10^{-6} C$ હશે.View Solution
- 6View Solutionકોષનો આંતરિક અવરોધ એ કોનો અવરોધ છે?
- 7એક બેટરીને બીજી $15\,V$ બેટરી વડે $8 $ કલાક ચાર્જ કરતાં $10\,A$ પ્રવાહ વહે છે. આ બેટરી જયારે ડિસ્ચાર્જ થાય છે,ત્યારે $5\,A$ નો પ્રવાહ $15$ કલાક સુધી વહે છે.ડિસ્ચાર્જ સમયે તેનો સરેરાશ ટર્મિનલ વોલ્ટેજ $ 14\,V$ રહે છે.આ બેટરીની $watt\, hour $ કાર્યક્ષમતા કેટલા $\%$ હશે?View Solution
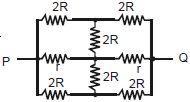
- 8પરિપથના $P$ અને $Q$ બિંદુ વચ્ચે સમતુલ્ય અવરોધ ......View Solution
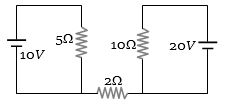
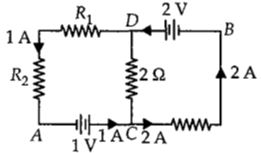
- 9આકૃતિમાં દર્શાવેલ પરિપથમાં બિંદુ $A$ આગળનું વિદ્યુતસ્થિતિમાન શૂન્ય હોય,તો બિંદુ $B $ આગળનું વિદ્યુતસ્થિતિમાન કેટલા ................ $V$ થાય?View Solution
- 10આપેલ પરિપથમાં $r$ ચલિત અવરોધ છે. જો $r = fR$ હોય ત્યારે $r$ માંથી મહત્તમ ઉષ્મા ઉત્પન્ન થતી હોય તો $f$ નું મૂલ્ય કેટલું હશે?View Solution