એક પ્રકાશકિરણ $\sqrt{3}$ જેટલો વક્રીભવાનાંક ધરાવતા કાંચની સપાટી પર $60^o$ ના કોણે આપાત થાય છે. વક્રીભુત અને પરાવર્તિત કિરણો વચ્ચેનો કોણ $ ........^o$ થશે.
NEET 2022, Medium
b
Method (i)
Method (i)
By Snell's law
\(1 \sin 60^{\circ}=\sqrt{3} \sin r\)
\(\frac{\sqrt{3}}{2}=\sqrt{3} \sin r\)
\(\sin r=\frac{1}{2}\)
\(r=30^{\circ}\)
Angle between refracted and reflected ray is \(90^{\circ}\)
Method \((ii)\)
Because angle of incidence is Brewster's angle so that angle between reflected and refracted ray is \(90^{\circ}\)
\(\operatorname{tani}_{p}=\mu=\sqrt{3}\)
\(i_{p}=60^{\circ}= i\)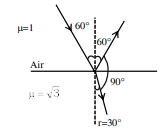
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક વસ્તુને અંતર્ગોળ અરિસાના વક્રતાકેન્દ્ર ${C}$ થી દૂર મૂકેલો છે. જો વસ્તુ અંતર ${C}$ થી ${d}_{1}$ અંતરે અને પ્રતિબિંબ ${C}$ થી ${d}_{2}$ અંતરે બને છે, તો અરિસાની વક્રતાત્રિજયા કેટલી હશે?View Solution
- 2એક સમઘન રૂમ અરીસાથી બનાવેલ છે.તળિયાના વિકર્ણ પર એક કીડી ગતિ કરે છે. ત્યારે બે અડકેલી દિવાલના અરીસામાં પ્રતિબિંબનો વેગ $10 cms^{-1}$ હોય,તો છતના અરીસામાં પ્રતિબિંબનો વેગ કેટલો થાય?View Solution
- 3$1.0$ અને $1.5$ વક્રિભવનાંક ધરાવતા બે પારદર્શક માધ્યમ $30\,cm$ વક્રતાત્રિજ્યાની ગોળીય વક્રીભવન સપાટી દ્વારા અલગ કરેલા છે. સપાટીનું વક્રતાકેન્દ્ર ધટ્ટ માધ્યમ તરફ રહેલું છે અને બિંદુવત્ વસ્તુને મુખ્ય અક્ષ પર સપાટીના ધ્રુવથી $15\,cm$ ના અંતરે પાતળા માધ્યમમાં મૂકેલ છે. સપાટીના ધ્રુવથી પ્રતિબિંબનું અંતર ........... $cm$ છે.View Solution
- 4$f $ કેન્દ્રલંબાઇ ધરાવતા બહિર્ગોળ અરીસાના ધ્રુવથી $f$ અંતરે વસ્તુ મૂકતાં પ્રતિબિંબ કયાં મળશે?View Solution
- 5સમતલ અરીસાથી $3\;m$ દૂર મૂકવામાં આવેલ પદાર્થના પ્રતિબિંબનો ફોટો લેવાનો છે. અરીસાથી $4.5 \;m$ અંતરે રહેલ કેમેરાને કેટલા.......$m$ અંતર માટે ફોકસ કરવું પડે?View Solution
- 6View Solutionઈલેક્ટ્રોન સુક્ષ્મદર્શક માટે, નીચેનામાંથી ક્યું સાચું છે ?
- 7$10\,\,cm$ કેન્દ્રલંબાઈના બહિર્ગોળ લેન્સના પ્રથમ કેન્દ્રબિંદુથી $5\,\, cm $ અંતરે પદાર્થ મૂક્લો છે. જો વાસ્તવિક પ્રતિબિંબ રચાતુ હોય તો તેનું લેન્સથી અંતર ........$cm$ છે.View Solution
- 8View Solutionનીચેનામાંથી ક્યું વિધાન સાચું છે ?
- 9એક માવલાવાળી લેન્સની ફોકલ લંબાઈ $(f)$ માપવા માટેના પ્રયોગમાં, પદાર્થની સ્થિતિ $(u)$ માટે અને પ્રતિબિંબની સ્થિતિ $(v)$ માટે માપન સ્કેલનો લઘુત્તમ ગણતરી ક્રમશ: $\Delta u$ અને $\Delta v$ છે. માવલાવાળી લેન્સની ફોકલ લંબાઈના માપમાં ભૂલ કેટલી હશે?View Solution
- 10View Solutionન્યૂનત્તમ વિચલનની સ્થિતિએ નિર્ગમન કોણ .......છે.
