એક સમતલ બર્હિગોળ લેન્સ એ એક સમતલ અંતર્ગોળ લેન્સમાં બરોબર બેસે છે. બંનેની સમતલ સપાટી એકબીજાને સમાંતર છે. જો લેન્સ ${\mu _1}$ અને${\mu _2}$ વક્રીભવનાંકવાળા ભિન્ન પદાર્થોના બનેલા હોય તથા તેમની વક્ર સપાટીની વક્રતા ત્રિજયા $R$ હોય, તો આવા સંયુકત લેન્સની કેન્દ્રલંબાઈ કેટલી થાય?
AIPMT 2013, Medium
c
The combination of two lenses \(1\) and \(2\) is as shown in figure.
The combination of two lenses \(1\) and \(2\) is as shown in figure.
\(\therefore \quad \frac{1}{f}=\frac{1}{f_{1}}+\frac{1}{f_{2}}\)
According to lens maker's formula
\(\frac{1}{{{f_1}}} = \left( {{\mu _1} - 1} \right)\left( {\frac{1}{\infty } - \frac{1}{{ - R}}} \right)\) \( = \frac{{\left( {{\mu _1} - 1} \right)}}{R}\)
\(\frac{1}{{{f_2}}} = \left( {{\mu _2} - 1} \right)\left( {\frac{1}{{ - R}} - \frac{1}{\infty }} \right)\)
\( = \left( {{\mu _2} - 1} \right)\left( { - \frac{1}{R}} \right)\) \( = - \frac{{\left( {{\mu _2} - 1} \right)}}{R}\)
\(\therefore \frac{1}{f} = \frac{{\left( {{\mu _1} - 1} \right)}}{R} - \frac{{\left( {{\mu _2} - 1} \right)}}{R}\)
\(\frac{1}{f} = \frac{{\left( {{\mu _1} - {\mu _2}} \right)}}{R};\) \(f = \frac{R}{{\left( {{\mu _1} - {\mu _2}} \right)}}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$3 cm$ જાડાઇ અને $3/2$ વક્રીવનાંક ધરાવતા કાંચને કાગળ પર રહેલા શાહીનું નિશાન પર મૂકવામાં આવે છે. તે નિશાનને $5 cm$ ઊંચાઇએથી જોતાં નિશાનનું પ્રતિબિંબ માણસની આંખથી કેટલા.....$cm$ અંતરે પડશે?View Solution
- 2જાંબલી અને લાલ રંગના વક્રીભવનાંક $1.54$ અને $1.52$ છે. જો પ્રિઝમનો પ્રિઝમકોણ $10^o $ હોય,તો કોણીય વિભેદન કેટલું થશે?View Solution
- 3ટેલિસ્કોપમાં ઓબ્જેક્ટિવ લેન્સની અને આઇપીસની કેન્દ્રલંબાઈ $15\;cm$ અને $10\;mm$ છે,જો ટ્યુબલંબાઈ $16\;cm$ હોય તો ટેલિસ્કોપની મોટવણી કેટલી થશે?View Solution
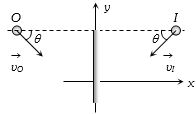
- 4જો એક વસ્તુ સમતલ અરીસાની તરફ $v$ વેગથી અરીસાની લંબ દિશા સાથે $\theta $ ખૂણે ગતિ કરે, તો તે વસ્તુ અને પ્રતિબિંબ વચ્ચેનો સાપેક્ષ વેગ કેટલો થાય?View Solution
- 5વક્રીભવનાંક વાળા પ્રિઝમ દ્વારા $\mu$ વિચલન પામે છે અને નાનો કોણ $A$ ને ............દ્વારા આપવામાં આવે છે.View Solution
- 6બીકરમાં પાણી$ h_1$ ઉંચાઈ સુધી અને પાણીની ઉપર $h_2$ ઉંચાઈ સુધી કેરોસીન ભરેલું છે. તેથી કુલ ઉંચાઈ (પાણી કેરોસીન) $(h_1 + h_2)$ છે. પાણીનો વક્રીભવનાંક $\mu_1$ અને કેરોસીનનો વક્રીભવનાંક $\mu_2$ છે. ઉપરથી બીકરનું તળિયું જોતાં તે કેટલી આભાસી સ્થિતિએ ખસેલું હશે?View Solution
- 7દિવાલથી $3 \,m$ અંતરે $3\, cm$ ઊંચાઇની મીણબત્તી મૂકેલી છે,દિવાલથી કેટલા......$cm$ અંતરે અંર્તગોળ અરીસો મૂકવાથી દિવાલ પર $9 \,cm$ ઊંચાઇનું પ્રતિબિંબ મળે?View Solution
- 8માછલી ઘરમાં પાણીની સપાટીથી $30\,cm$ ઊંડાઈએ રહેલી માછલી પાણીની સપાટી થી $50\,cm$ ઊંચાઈએ રહેલા બલ્બને જોઈ શકે છે. આ માછલી બલ્બનું પ્રતિબિંબ પણ જોઈ શકે છે. પાણીની કુલ ઊંડાઈ $60\,cm$ છે. માછલી ને દેખાતા બન્ને પ્રતિબિંબ વચ્ચેનું અંતર.View Solution
- 9ગોળાકાર અરીસા તરફ પ્રકાશીય બિંદુ તેની અક્ષ પર $v_0$ ઝડપથી ગતિ કરે છે. પ્રતિબિંબની ઝડપ કેવી રીતે આપવામાં આવે છે? ( $r =$ વક્રતા ત્રિજ્યા, $u =$ અંતર)View Solution
- 10$15\, cm $ કેન્દ્રલંબાઈના બહિર્ગોળ અરીસા અને $10\, cm$ લંબાઈના અંત:ર્ગોળ અરીસાને એકબીજાથી સામ સામે $40\, cm$ અંતરે મૂકેલા છે. એક બિંદુવત્ વસ્તુને અરીસાઓની વચ્ચે તેઓની સામાન્ય અક્ષ પર અને અંત:ર્ગોળ અરીસાથી $15\, cm$ ના અંતરે મૂકવામાં આવે છે. પરાવર્તન દ્વારા ઉત્પન્ન થતાં પ્રતિબિંબનું સ્થાન બહિર્ગોળ અરીસા પાસે .....$cm$ અંતરે હશે.View Solution
