ગોળાકાર અરીસા તરફ પ્રકાશીય બિંદુ તેની અક્ષ પર $v_0$ ઝડપથી ગતિ કરે છે. પ્રતિબિંબની ઝડપ કેવી રીતે આપવામાં આવે છે? ( $r =$ વક્રતા ત્રિજ્યા, $u =$ અંતર)
Medium
Download our app for free and get started
d
\(\frac{1}{v}+\frac{1}{u}=\frac{1}{f}\)
\(\frac{1}{v}+\frac{1}{u}=\frac{1}{f}\)
Differentiating both sides \(-\frac{1}{v^2} \frac{d v}{d t}=\frac{1}{u^2} \frac{d u}{d t}\)
\(\frac{d v}{d t}=v_l=-\left(\frac{v}{u}\right)^2 \frac{d u}{d t}=-\left(\frac{v}{u}\right)^2 v_0\)
Again \(\frac{1}{v}=\frac{1}{f}-\frac{1}{u}=\frac{2}{r}-\frac{1}{u}=\frac{2 u-r}{r u}\)
\(v=\frac{u r}{2 u-r}\)
\(v_i=-\left(\frac{v}{u}\right)^2 v_o=-v_o\left(\frac{r}{2u-r}\right)^2\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionલઘુદ્રષ્ટિની ખામીવાળા માણસમાં વસ્તુનું પ્રતિબિંબ કયાં પડે?
- 2$15\, cm$ કેન્દ્રલંબાઈના અંતર્ગોળ અરીસાથી રચાતા પ્રતિબિંબનું રેખીય પરિમાણ તે પદાર્થથી બમણું છે. જો પ્રતિબિંબ આભાસી હોયતો પદાર્થનું સ્થાન ......$cm$ હશે.View Solution
- 3લેન્સના સંયોજન વડે ૨ચાતા પ્રતિબંબનું સ્થાન. . . . . છે. $\mathrm{f}_1=10 \mathrm{~cm} \quad \mathrm{f}_2=10 \quad \mathrm{f}_3=30 \mathrm{~cm}$View Solution
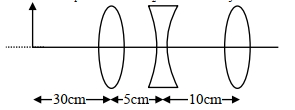
- 4આકૃતિમાં દર્શાવેલ લેન્સના સંયોજનથી કયા સ્થાન પર અને કેવું પ્રતિબિંબ રચાશે? ($f_1, f_2$ એ કેન્દ્ર લંબાઈ છે.)View Solution
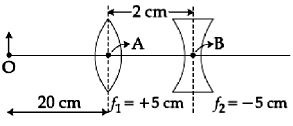
- 5પ્રકાશનું કિરણ $\mu$ વક્રીભવનાંક ધરાવતા માધ્યમમાંથી હવામાં ગતિ કરે છે.તા વિચલનકોણ ($\delta$ ) અને આપાતકોણ $(i)$ નો આલેખ કેવો થાય?View Solution
- 6વ્યક્તિએ સાદા ચશ્માં પહેરેલા છે,તેમાં કાચ અને આંખ વચ્ચે $2$ સેમીનું અંતર છે. તેનો પાવર $-5\,D$ છે. જો તે કોન્ટેકટ લેન્સ પહેરે તો તેનો પાવર ($D$ માં) કેટલો હશે?View Solution
- 7$20\;cm$ કેન્દ્રલંબાઈ ધરાવતા દ્વિ-બર્હિગોળ લેન્સને $1.5$ વક્રીભવનાંક ધરાવતા કાંચમાંથી બનાવેલો છે. જ્યારે તેને પાણીમાં ${(_a}{\mu _w} = 4/3)$ સંપૂર્ણ ડુબાડવામાં આવે ત્યારે તેની કેન્દ્રલંબાઇ ($cm$ માં) કેટલી થાય?View Solution
- 8શરૂઆતમાં સમાંતર એવું નળાકાર કિરણજૂથ $\mu( I )=\mu_{0}+\mu_{2} I$ ધન વક્રીભવનાંકવાળા માધ્યમમાં પસાર થાય છે. અહી $\mu_{0}$ અને $\mu_{2}$ એ ધન અચળાંકો છે અને $I$ એ કિરણજૂથની તીવ્રતા છે. ત્રિજ્યામાં વધારા સાથે કિરણજૂથની તીવ્રતામાં ઘટાડો થાય છે.View Solution
આ માધ્યમમાં પ્રકાશની ગતિ
- 9લેન્સના સંયોજન વડે ૨ચાતા પ્રતિબંબનું સ્થાન. . . . . છે. $\mathrm{f}_1=10 \mathrm{~cm} \quad \mathrm{f}_2=10 \quad \mathrm{f}_3=30 \mathrm{~cm}$View Solution
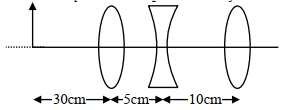
- 10તેજસ્વી પ્રકાશ ઉદગમથી $10\ cm$ દુર રાખેલ બહિર્ગોળ લેન્સ તેનાથી $10\ cm$ દુર રાખેલ પડદા પર તીવ્ર (સ્પષ્ટ) પ્રતિબિંબ બનાવે છે. $1.5\ cm$ જાડાઇવાળા એક કાચના ચોસલા (જેનો વક્રીભવનાંક $1.5$ છે)ને પ્રકાશ ઉદગમની ઊપર મુકવવામાં આવે છે. ફરી તીવ્ર (સ્પષ્ટ) પ્રતિબિંબ મેળવવા માટે પડદાને $d$ અંતરે ખસેડવામાં આવે છે. તો $d$ કેટલો હશે?View Solution