એક સરળ આવર્ત ગતિ કરતાં પદાર્થ માટે આવર્તકાળ $T\, = 0.5\, s$ અને કંપવિસ્તાર $A\,= 1\, cm$ છે. જ્યારે પદાર્થ પોતાના સમતોલન સ્થાન પરથી અડધા કંપવિસ્તાર સુધી ગતિ કરે તે દરમિયાન તેનો સરેરાશ વેગ $cm/s$ માં કેટલો મળે?
JEE MAIN 2014, Medium
c
Given: Time period, \(T=0.5\) sec
Given: Time period, \(T=0.5\) sec
Amplitude, \(\mathrm{A}=1 \mathrm{cm}\)
Average velocity in the interval in which body moves from equilibrium to half of its amplitude, \(\mathrm{v}=?\)
Time taken to a displacement \(A/2\) where \(A\) is the amplitude of oscillation from the
mean position \(^{\prime} \mathrm{O}^{\prime}\) is \(\frac{\mathrm{T}}{12}\)
Therefore, time, \(t=\frac{0.5}{12} \mathrm{sec}\)
Displacement, \(s=\frac{A}{2}=\frac{1}{2} c m\)
Average velocity, \(v=\frac{\frac{A}{2}}{t}=\frac{\frac{1}{2}}{\frac{0.5}{12}}=12 \mathrm{cm} / \mathrm{s}\)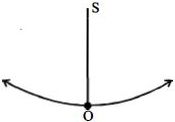
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionજ્યારે કણ સમતોલન સ્થાન અને અંતિમ બિંદુ વચ્ચે હોય ત્યારે કુલ યાંત્રિક ઉર્જાની કેટલામાં ભાગની ઉર્જા ગતિઉર્જા સ્વરૂપે હશે?
- 2$0.05$ મી કંપ વિસ્તાર ધરાવતી સરળ આવર્ત ગતિનું સ્થાનાંતર $0.01$ મી હોય ત્યારે પ્રવેગ $1.0 \,m / s ^{2}$ છે,તો તેનો આવર્તકાળ કેટલો હશે?View Solution
- 3વિધેય $sin^2\,(\omega t)$ શું દર્શાવે છે?View Solution
- 4$1\, s$ આવર્તકાળ ધરાવતું લોલક આવામંદનને કારણે ઉર્જા ગુમાવે છે.એક સમયે તેની ઉર્જા $45\, J$ છે જો $15 $ દોલનો પછી તેની ઉર્જા $15\, J$ થતી હોય તો અવમંદનનો અચળાંક (damping constant$=\frac bm$) ($s^{-1}$ માં) કેટલો થાય?View Solution
- 5સરળ આવર્ત ગતિ કરતા કણનો વેગ સ્થાનાંતર $(x)$ સાથે $4 v^2=50-x^2$ અનુસાર બદલાય છે. દોલનોનો આવર્તકાળ $\frac{x}{7}$ છે. તો $x$ નું મૂલ્ય $............$ છે.View Solution
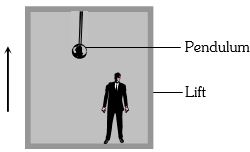
- 6સ્થિર લિફ્ટમાં સાદા લોલકનો આવર્તકાળ $T$ છે,હવે લિફ્ટ $ \frac{g}{4} $ ના પ્રવેગથી ઉપર તરફ ગતિ કરે,તો નવો આવર્તકાળ કેટલો થાય?View Solution
- 7$A$ જેટલો આડછેદ ધરાવતા એક સમાંગ તારમાંથી બનાવેલા સાદા લોલકનો આવર્તકાળ $T$ છે.જયારે વધારાનું દળ $M$ દોલકમાં ઉમેરવામાં આવે છે,ત્યારે તેનો આવર્તકાળ બદલાઇ $TM$ થાય છે.જો તારના દ્વવ્ય માટે યંગનો સ્થિતિસ્થાપકતા અંક થ હોય,તો $\frac{1}{Y}$ _______ જેટલો થશે. ( $g$ ગુરુત્વીય પ્રવેગ છે.)View Solution
- 8જ્યારે કણ અંતિમ બિંદુ કરતાં અડધા અંતરે હોય ત્યારે સરળ આવર્ત ગતિ કરતાં કણની સ્થિતિ ઊર્જા કેટલી થાય? (જ્યાં $E$ કુલઊર્જા છે.)View Solution
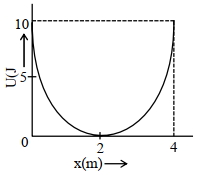
- 9$5\, {kg}$ દળને સ્પ્રિંગ સાથે જોડેલ છે. આ તંત્ર દ્વારા થતી સરળ આવર્તગતિની સ્થિતિઊર્જાનો ગ્રાફ આકૃતિમાં દર્શાવેલ છે. $4\, {m}$ લંબાઈના સાદા લોલકનો આવર્તકાળ સ્પ્રિંગતંત્રના આવર્તકાળ જેટલો જ છે. જ્યાં આ પ્રયોગ કરવામાં આવેલ છે તે ગ્રહ પર ગુરુત્વપ્રવેગનું મૂલ્ય (${m} / {s}^{2}$ માં) કેટલું હશે?View Solution
- 10સરળ આવર્તગતિનું સમીકરણ $y = 0.30\sin (220\,t + 0.64)\ m$ હોય,તો આવૃતિ અને મહત્તમ વેગ અનુક્રમે કેટલા થાય?View Solution
