સ્થિર લિફ્ટમાં સાદા લોલકનો આવર્તકાળ $T$ છે,હવે લિફ્ટ $ \frac{g}{4} $ ના પ્રવેગથી ઉપર તરફ ગતિ કરે,તો નવો આવર્તકાળ કેટલો થાય?
Medium
Download our app for free and get started
c
(c) In stationary lift \(T = 2\pi \sqrt {\frac{l}{g}} \)
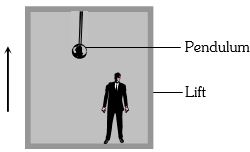
(c) In stationary lift \(T = 2\pi \sqrt {\frac{l}{g}} \)
In upward moving lift \(T' = 2\pi \sqrt {\frac{l}{{(g + a)}}} \) (\(a = \)Acceleration of lift)
\( \Rightarrow \frac{{T'}}{T} = \sqrt {\frac{g}{{g + a}}} = \sqrt {\frac{g}{{\left( {g + \frac{g}{4}} \right)}}} = \sqrt {\frac{4}{5}} \)
\( \Rightarrow T' = \frac{{2T}}{{\sqrt 5 }}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
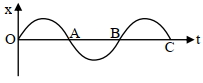
- 1સરળ આવર્તગતિ કરતાં કણ માટે સમય સાથે સ્થાનાંતરનો ફેરફર આકૃતિમાં દર્શાવેલ છે. તો સ્થિતિઉર્જા ${U}({x})$ નો સમય $({t})$ વિરુદ્ધનો ગ્રાફ કેવો મળે?View Solution
- 2ધાતુનો ગોળો ધરાવતું એક લોલક $T$ જેટલો આવર્તકાળ ધરાવે છે. હવે આ ગોળાને અસ્નિગ્ધ પ્રવાહીમાં ડુબાડી રાખીને દોલનો કરાવવામાં આવે છે. જો આ પ્રવાહીની ઘનતા ગોળાની ઘનતા કરતાં $1 / 4$ જેટલી હોય તો આ લોલકનો આવર્તકાળ કેટલો થશે ?View Solution
- 3$K _{1}$ અને $K _{2}$ બળઅચળાંક ધરાવતી સ્પ્રિંગના છેડે બે સમાન દળના કણ $A$ અને $B$ લગાવીને દોલનો કરવવામાં આવે છે. જો તેમનો મહત્તમ વેગ સમાન હોય તો $A$ અને $B$ ના કંપવિસ્તારનો ગુણોત્તર કેટલો થાય?View Solution
- 4બે સરળ આવર્તગતિને નીચે મુજબ આપવામાં આવે છે.View Solution
${y}_{1}=10 \sin \left(3 \pi {t}+\frac{\pi}{3}\right)$
$y_{2}=5(\sin 3 \pi t+\sqrt{3} \cos 3 \pi t)$
${y}_{1}$ અને ${y}_{2}$ ના કંપવિસ્તારનો ગુણોતર ${x}: 1$ હોય તો ${x}$ નું મૂલ્ય કેટલું હશે?
- 5View Solutionએક રોકેટમાં સેકન્ડ લોલક રાખેલું છે. તેના દોલનોનો આવર્તકાળ ઘટે જ્યારે રોકેટ .......
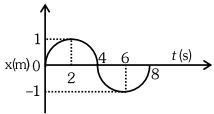
- 6સરળ આવર્તગતિ કરતા કણનો $x$ - $t$ આલેખ આકૃતિમાં દર્શાવેલો છે. $t=2$ સેકન્ડ વખતે કણનો પ્રવેગ $.......$ છે.View Solution
- 7$m$ દળ ધરાવતો કણView Solution
$x = x_0 + a\, cos\,\omega_1 t$
$y = y_0 + b\, sin\,\omega_2t$
મુજબ ગતિ કરે,તો $t = 0$ સમયે ઉગમબિંદુ આગળ કણ પર કેટલું ટોર્ક લાગતું હશે?
- 8અવમંદિત સરળ આવર્ત ગતિ કરતાં દોલનોની આવૃતિ $5$ દોલનો પ્રતિ સેકન્ડ છે.દર $10$ દોલનોમાં તેનો કંપવિસ્તાર અડધો થાય છે.તેનો કંપવિસ્તાર $\frac{1}{1000}$ થવા માટે કેટલો .... $s$ સમય લાગે?View Solution
- 9બે સરળ આવર્તગતિ નીચેના સમીકરણ મુજબ આપવામાં આવે છે.View Solution
${x}_{1}=5 \sin \left(2 \pi {t}+\frac{\pi}{4}\right)$ અને ${x}_{2}=5 \sqrt{2}(\sin 2 \pi {t}+\cos 2 \pi {t})$
બીજી ગતિનો કંપવિસ્તાર પહેલી ગતિ કરતાં કેટલા ગણો હશે?
- 10$m$ દળને શિરોલંબ નહિવત દળ ધરાવતી સ્પ્રિંગ સાથે લટકાવેલ છે, આ તંત્ર $n$ આવૃતિથી દોલનો કરે છે. જો $4m$ દળને સમાન સ્પ્રિંગ સાથે લટાવવામાં આવે, તો તંત્રની આવૃતિ કેટલી થાય?View Solution