એક યંગના ડબલ સ્લિટ પ્રયોગમાં, $\lambda=5000\; \mathring A$ ના તરંગલંબાઈનો પ્રકાશ વપરાય છે. $d=3 \times 10^{-7}\,m$ એ રાખેલી સ્લીટમાંથી ઉદ્ભવે છે. $t=1.5 \times 10^{-7}\,m$ ની તથા વકીભવનાંક $\mu=1.17$ ધરાવતી પારદર્શી શીટને એક પર મૂકવામા આવે છે. પડદાના મધ્યમાંથી રચના મધ્ય અધિક્તમનીનો નવી કોણીય સ્થાન જણાવો અને $y$ નું મૂલ્ય શોધો.

Diffcult
b
(b)
(b)
The path difference when transparent sheet is introduced \(\Delta x=(\mu-1) t\)
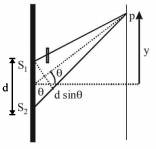
If the central maxima occupies position of nth fringe, then \((\mu-1) t=n \lambda=d \sin \theta\)
\(\Rightarrow \sin \theta =\frac{(\mu-1) t }{ d }\)
\(=\frac{(1.17-1) \times 1.5 \times 10^{-7}}{3 \times 10^{-7}}=0.085\)
Therefore, angular position of central maxima \(\theta=\sin ^{-1}(0.085)=4.88^{\circ} \approx 4.9\)
For small angles, \(\sin \theta \approx \theta \approx \tan \theta\)
\(\Rightarrow \quad \tan \theta=\frac{y}{D}\)
\(\therefore \quad \frac{y}{D}=\frac{(\mu-1) t}{d} \Rightarrow y=\frac{D(\mu-1) t}{d}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1પૃથ્વી દૂર ખસતા તારામાથી આવતા પ્રકાશની આભાસી તરંગલંબાઈ તેની વાસ્તવિક તરંગલંબાઈ કરતા $0.02\,\%$ વધુ છે. તારાનો વેગ કેટલો ........ $km / s$ છે.View Solution
- 2$2500\,\mathop A\limits^o $ અને $3500\,\mathop A\limits^o$ તરંગલંબાઈ ધરાવતા પ્રકાશના બે સ્ત્રોતનો ઉપયોગ યંગના ડબલ સ્લીટના પ્રયોગમાં એકસાથે થાય છે. આ બે તરંગલંબાઈ ની કયા ક્રમની શલાકા એકબીજા સાથે એકરૂપ થશે?View Solution
- 3સરખી તીવ્રતા ધરાવતા બે સુસમ્બ્ધ તરંગો મહત્તમ $100$ એકમ ઉત્પન્ન કરે છે. જો તે બન્ને ઉદ્દગમોમાંથી એકની તીવ્રતા $ 20\%$ જેટલી ઘટાડવામાં આવે તો, મહત્તમ તીવ્રતા .....View Solution
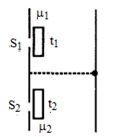
- 4યંગના બે સ્લિટના પ્રયોગમાં $1.2\, \mu m$ જાડાઈ ધરાવતી $1.5 $ જેટલો વક્રીભવનાંક ધરાવતો કાચનો સ્લેબ એક સ્લીટની આગળ મૂકવામાં આવે છે. જ્યારે બીજો સ્લેબ કે જે $ t$ જાડાઈ અને વક્રીભવનાંક $ 2.5$ ધરાવે છે. તેને બીજી સ્લીટ આગળ મૂકવામાં આવે છે. જો કેન્દ્રીય શલાકાની સ્થિતિ બદલાતી ન હોય, તો જાડાઈ $t $......$\mu m$View Solution
- 5સફેદ પ્રકાશ $4/3 $ વક્રીભવનાંક ધરાવતી સાબુની ફિલ્મ પર $ 30^o$ ના ખૂણે આપાત થાય છે. પારગમિત પ્રકાશની તરંગલંબાઈ $6 \times 10^{-5}\, cm$ જોવામાં આવી છે. ફિલ્મની ન્યૂનત્તમ જાડાઈ શોધો.View Solution
- 6$0.6 \times 10^{-4}\, m$ પહોળાઈ ધરાવતી સ્લિટ પર $6000 \times 10^{-10}\, m$ તરંગલંબાઈ ધરાવતો પ્રકાશ આપાત કરવામાં આવે છે મધ્યસ્થ અધિકતમની બંને બાજુ મહતમ ન્યુનતમોની સંખ્યાView Solution
- 7પ્રકાશનુંં વ્યતિકરણ સતત મેળવવા માટેની બે શરતો લખો. યંગના દ્વિ સ્લીટ પ્રયોગમાં,$ 400 \,nm, $ તરંગલંબાઈનો પ્રકાશ લેતાં $'X' $ પહોળાઈની વ્યતિકરણ શલાકાઓ મળે છે. પ્રકાશની તરંગલંબાઈ $600 \,nm$ સુધી વધારતા અને સ્લીટો વચ્ચેનું વિયોજન અડધુ કરવામાં આવે છે. જો પડદા પર મળતી શલાકાની પહોળાઈ બન્ને ઘટનાઓમાં સરખી અનુભવવા મળે તો બંને ગોઠવણીમાંના પડદા અને સ્લીટો વચ્ચેના અંતરનો ગુણોત્તર શોધો.View Solution
- 8યંગના પ્રયોગમાં સફેદ પ્રકારનો ઉપયોગ કરવામાં આવે છે. બે સ્લિટ વચ્ચેનું અંતર $b$ છે.સ્લિટ અને પડદા વચ્ચે નું અંતર $d (d>> b)$ છે. સ્લિટની બરાબર સામે ગેરહાજર તરંગલંબાઈView Solution
- 9યંગના ડબલ સ્લિટના પ્રયોગમાં $6000 Å $ તરંગલંબાઇવાળો પ્રકાશ વાપરવામાં આવે છે.પડદા પરના $P$ બિંદુએ ત્રીજી અપ્રકાશિત શલાકા રચાય છે,તો પથ તફાવત $S_1P -S_2P$ માઇક્રો મીટરમાં કેટલો થાય?View Solution
- 10યંગના ડબલ સ્લિટના પ્રયોગમાં $4800 \,\mathop A\limits^o $ તરગલંબાઈનો પ્રકાશ વાપરવામાં આવેલ છે. એક સ્લિટને $1.4$ વક્રીભવનાંકવાળી પાતળી પારદર્શક પ્લેટ વડે ઢાંકવામાં આવે અને બીજી સ્લિટને $1.7$ વક્રીભવનાંકવાળી બીજી પાતળી પારદર્શક પ્લેટ વડે ઢાંકવામાં આવે છે. પરિણામે કેન્દ્રથી પહેલા જેટલા અંતરે પાંચમી પ્રકાશિત શલાકા રચાતી હતી, ત્યાં મધ્યસ્થ પ્રકાશિત શલાકા શિફટ થાય છે, તો બંને પાદર્શક પ્લેટની જાડાઈ .......$\mu m$View Solution
