હાઈડ્રોજન વર્ણપટમાં બામર શ્રેણીની સૌથી ટૂંકી તરંગલંબાઈ $\lambda$ છે. તો બ્રેકેટ શ્રેણીની સૌથી ટૂંકી તરંગલંબાઈ $.......\,\lambda$ છે.
NEET 2023, Medium
c
Shortest wavelength in Balmer series when transition of \(e^{-}\)from \(\infty\) to \(n=2\)
Shortest wavelength in Balmer series when transition of \(e^{-}\)from \(\infty\) to \(n=2\)
\(\because \frac{1}{\lambda}= Rz ^2\left[\frac{1}{2^2}-\frac{1}{\infty^2}\right]\)
\(\frac{1}{\lambda}=\frac{ R }{4}\)
Shortest wavelength is Bracket series when transition of \(e^{-}\)from \(\infty\) to \(n=4\)
\(\frac{1}{\lambda^{\prime}}= R (1)^2\left[\frac{1}{4^2}-\frac{1}{\infty^2}\right] \Rightarrow \frac{1}{\lambda^{\prime}}=\frac{ R }{16}\)
Eq. \((1)\)/Eq.\((2)\)
\(\frac{\lambda^{\prime}}{\lambda}=\frac{R}{4} \times \frac{16}{R} \Rightarrow \lambda^{\prime}=4 \lambda\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionનીચેનામાંથી કઈ સંક્રાંતિ દરમિયાન હાઈડ્રોજન પરમાણુ માટે મહતમ આવૃતિવાળા ફોટોન ઉત્સર્જિત થાય?
- 2હાઈડ્રોજન પરમાણુમાં $n =3$ કક્ષામાં રહેલા ઇલેક્ટ્રોનનાં કારણે કેન્દ્ર પર ચુંબકીય ક્ષેત્ર ($T$ માં) શું હશે?View Solution
- 3સોડિયમ (પરમાણુ કર્માંક $= 11$) ની બીજી કક્ષામાં રહેલા ઇલેકટ્રોનનો વેગ $v$ છે, તો $5$ મી કક્ષામાં રહેલા ઇલેકટ્રોનનો વેગ કેટલો થાય?View Solution
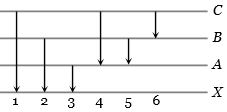
- 4નીચે આપેલ આકૃતિમાં પરમાણુ માટે ઉર્જાસ્તર અને તેના ઉત્સર્જનની છ વર્ણપટ્ટ રેખા દર્શાવેલ છે ($5$ નંબરની રેખા $ B$ સ્તરથી $A$ સ્તર પરની સંક્રાંતિ દર્શાવે છે) તો તેમાંથી કઈ વર્ણપટ્ટ રેખા શોષણ વર્ણપટ્ટમાં પણ દેખાશે?View Solution
- 5ઓરડાના તાપમાને વાયુ સ્વરૂપ હાઇડ્રોજનને પ્રતાડિત કરવા માટે $12.5\,eV$ નું ઈલેકટ્રોન પુંજ વાપરવામાં આવે છે. ઉત્સર્જિત વર્ણપટ રેખાઓની સંખ્યા $.......$ હશે.View Solution
- 6હાઈડ્રોજન વર્ણપટમાં લાયમન્ શ્રેણીમાં નાનામાં નાની તરંગલંબાઈ $915 \mathring A$ છે. બામર શ્રેણીમાં વર્ણપટ રેખાની તરંગલંબાઈ. . . . . . $\mathring A$ હશે.View Solution
- 7પરમાણુ ક્રમાંક $43$ ની $K_\alpha$ રેખાની તરંગલંબાઈ છે. તો પરમાણુ ક્રમાંક $29$ ની $K_\alpha$ રેખાની તરંગલંબાઈ કેટલી થશે?View Solution
- 8એક પરમાણુની કોઈ એક કક્ષામાં ઈલેક્ટ્રોનની કુલ ઊર્જા $-3.4\;eV$ છે. તેની ગતિ અને સ્થિતિઊર્જાઓ અનુક્રમે શું થાય?View Solution
- 9હાઇડ્રોજન પરમાણુમાં $3$ ની કક્ષામાંથી $2$ ની કક્ષામાં સંક્રાતિ દરમિયાન ઉત્સર્જિત થતી તરંગલંબાઇ ${\lambda _0}$ છે,તો $4$ ની કક્ષામાંથી $2$ ની કક્ષામાં સંક્રાતિ દરમિયાન કેટલી તરંગલંબાઇનું ઉત્સર્જન થાય?View Solution
- 10$5 × 10^{-3}\, m$ જાડાઈના સોનાની ફિલ્મ પસાર કર્યા પછી ક્ષ કિરણની પ્રારંભિક તીવ્રતા કરતાં ક્ષ કિરણ પુંજની તીવ્રતા $36.8\%$ જેટલી ઘટે તો તેનો શોષણ ગુણાંક .......$m^{-1}$ છે.View Solution
