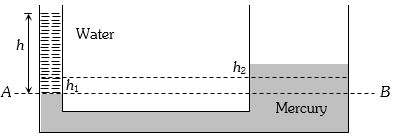
જમણી બાજુના આડછેદનો વ્યાસ , ડાબી બાજુના આડછેદનો વ્યાસ કરતાં $n $ ગણો છે.સાંકડી બાજુમાં $ h$ ઊંચાઇ સુધી પાણી ભરેલ છે,જમણી બાજુમાં મરકયુરી ઊંચાઇ કેટલી વધે? ($s =$ મરકયુરીની સાપેક્ષ ઘનતા અને$\rho $ $= $ પાણીની ધનતા )


Diffcult
b
(b)If the level in narrow tube goes down by \(h_1\) then in wider tube goes up to \(h_2,\)
Now, \(\pi {r^2}{h_1} = \pi {(nr)^2}{h_2}\)==> \({h_1} = {n^2}{h_2}\)
Now, pressure at point A = pressure at point B
\(h\rho g = ({h_1} + {h_2})\rho 'g\)
==> \( h = \) \(({n^2}{h_2} + {h_2})sg\) \(\left( {{\rm{As}}\;s = \frac{{\rho '}}{\rho }} \right)\) ==> \({h_2} = \frac{h}{{({n^2} + 1)s}}\)
(b)If the level in narrow tube goes down by \(h_1\) then in wider tube goes up to \(h_2,\)
Now, \(\pi {r^2}{h_1} = \pi {(nr)^2}{h_2}\)==> \({h_1} = {n^2}{h_2}\)
Now, pressure at point A = pressure at point B
\(h\rho g = ({h_1} + {h_2})\rho 'g\)
==> \( h = \) \(({n^2}{h_2} + {h_2})sg\) \(\left( {{\rm{As}}\;s = \frac{{\rho '}}{\rho }} \right)\) ==> \({h_2} = \frac{h}{{({n^2} + 1)s}}\)

Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1સ્ટોક્સના નિયમની સકાચણી કરવા માટે કરેલા પ્રયોગમાં $r$ ત્રિજ્યા અને $\rho$ ઘનતા ધરાવતા એક ગોળ દડાને પાણી ભરેલા પાત્રમાં પાણીની સપાટીથી $h$ ઊંચાઈ પરથી મુક્ત કરવામાં આવે છે. જો પાણીની અંદર દડાનો ટર્મિનલ વેગ એ પાણીની અંદર આવતા પહેલા દડાના વેગ જેટલો હોય તો ઊંચાઈ $h$ કોના સમપ્રમાણમાં હશે? (હવાનો શ્યાનતાગુણાંક અવગણો)View Solution
- 2પાણી ભરેલા પાત્રમાં તળિયે છિદ્ર પાડતાં $10 min $ માં પાત્ર ખાલી થાય છે,જો પાત્ર અડધું ભરેલું હોય,તો ખાલી થતાં ...... $\min$ લાગે.View Solution
- 3એક હાઈડ્રોલિક લીફટની $5000\,kg$ દળના વાહનને ઉંયકવા માટે રચના કરેલી છે. વજન ઉંચકતા નળાકારના આડછેદનું ક્ષેત્રફળ $250\,cm ^2$ છે. નાના પિસ્ટન દ્વારા અનુભવાતુ મહત્તમ દબાણ $........$ છે [$g =10\,m / s ^2$ ધારો.]View Solution
- 4$60\, kg$ દળ ધરાવતો છોકરો નદીમાં લાકડાના સહારે તરવા માંગે છે.જો લાકડાની સાપેક્ષ ઘનતા $0.6$ હોય તો લાકડાનું ઓછામાં ઓછું કદ કેટલું હોવું જોઈએ? (નદીના પાણીની ઘનતા $1000\, kg/m^3$)View Solution
- 5$M$ દળ ધરાવતા અને $d$ જેટલી ઘનતા ધરાવતા એક નાના બોલ (દડા) ને, ગ્લીસરીન ભરેલા પાત્રમાં પતન કરવામાં આવે છે ત્યારે તેની ઝડપ અમુક સમય બાદ અચળ થાય છે. જે ગ્લિસરીનની ધનતા $\frac{\mathrm{d}}{2}$ જેટલી હોય તો દડા પર લાગતું સ્નિગ્ધતા (શ્યાનતા) બળ $....$ હશે.View Solution
- 6એક વિમાન અચળ ઝડપથી સમક્ષિતિજ ઉડ્ડયનમાં છે અને બેમાંની દરેક પાંખનું ક્ષેત્રફળ $25\, m^2$ છે. જો પાંખની નીચેની સપાટીએ વેગ $180\, km/h$ અને ઉપરની સપાટીએ વેગ $234\, km/h$ હોય, તો વિમાનનું દળ શોધો. (હવાની ઘનતા $1 \,kg\, m^{-3}$ લો .)View Solution
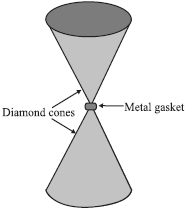
- 7હીરાના એક જ સ્ફટિકમાંથી આકૃતિમાં દર્શાવ્યા મુજબના આકારનું એરણ (anvils) બનાવેલ છે. તેનો ઉપયોગ ઊંચા દબાણ હેઠળ દ્રવ્યની વર્તણૂક તપાસવા માટે થાય છે. એરણના સાંકડા છેડા પાસે સપાટ બાજુઓના વ્યાસ $0.50\, mm$ છે. જો એરણના પહોળા છેડાઓ પર $50,000\, N$ નું દાબીય બળ લાગુ પાડેલ હોય, તો એરણના સાંકડા છેડે (tip) દબાણ કેટલું હશે.View Solution
- 8બે નાના સમાન દળના અને $\rho_{1}$ અને $\rho_{2}\left(\rho_{1}=8 \rho_{2}\right)$ ઘનતા ધરાવતા ગોળાની ત્રિજ્યા અનુક્રમે $1\; mm$ અને $2\; mm$ છે. તે બંનેને એક $\eta$ શ્યાનતાગુણાંક વાળા અને $0.1{\rho}_{2} $ ઘનતા ધરાવતા પ્રવાહીમાં (સ્થિર સ્થિતિમાંથી) પાડવામાં આવે, તો તેમના ટર્મિનલ વેગનો ગુણોત્તર કેટલો થાય?View Solution
- 9પાણીની અંદર $1\,cm$ ત્રિજ્યાના હવાના પરપોટાનો ઉપરની દિશામાંનો પ્રવેગ $9.8\, cm\, s ^{-2}$ છે. પાણીની ઘનતા $1\, gm\, cm ^{-3}$ અને પાણી દ્વારા પરપોટા પર નહિવત ઘર્ષણબળ લાગે છે. તો પરપોટાનું દળ $.......gm$ હશે.View Solution
$\left( g =980 \,cm / s ^{2}\right)$
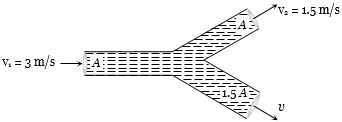
- 10આકૃતિમાં પ્રવાહીનો વેગ $ v= $......... $m/s$View Solution